Mathematics
Answer
We know that,
The locus of point equidistant from two points is the perpendicular bisector of the line joining those points.
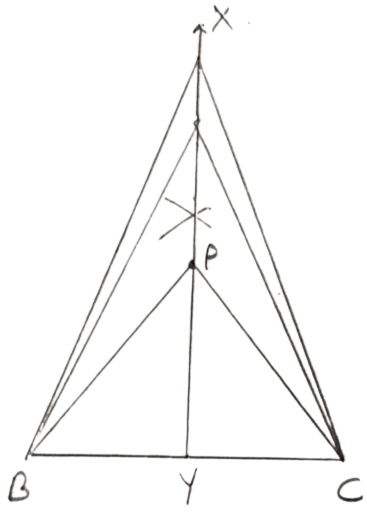
Steps of construction :
Draw a line segment BC (common base)
Draw XY, perpendicular bisector of BC.
Mark point P on XY.
So, PB = PC as P lies on perpendicular bisector of BC.
Hence, the locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
Related Questions
Describe the locus of a point P, so that :
AB2 = AP2 + BP2,
where A and B are two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC.
(ii) B and D.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of the centers of all circles passing through two fixed points.