Mathematics
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC.
(ii) B and D.
Locus
6 Likes
Answer
(i) We know that,
The locus of a point, which is equidistant from two intersecting straight lines, is a line which bisects the angle between the given lines.
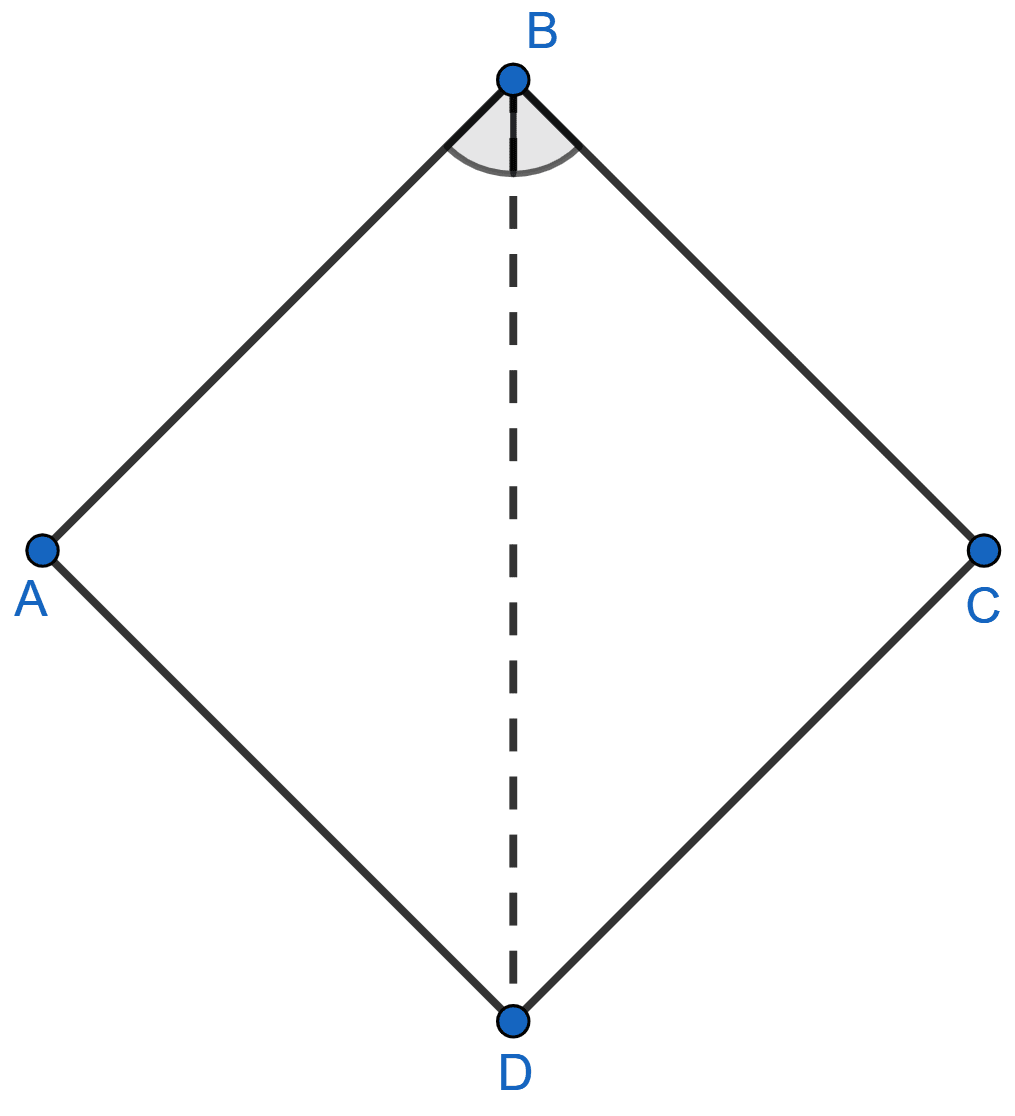
In rhombus,
The diagonals bisect the interior angles.
Hence, the locus of point in a rhombus ABCD which is equidistant from AB and BC will be the diagonal BD.
(ii) We know that,
The locus of a point, which is equidistant from two points is the perpendicular bisector of the line joining those points.
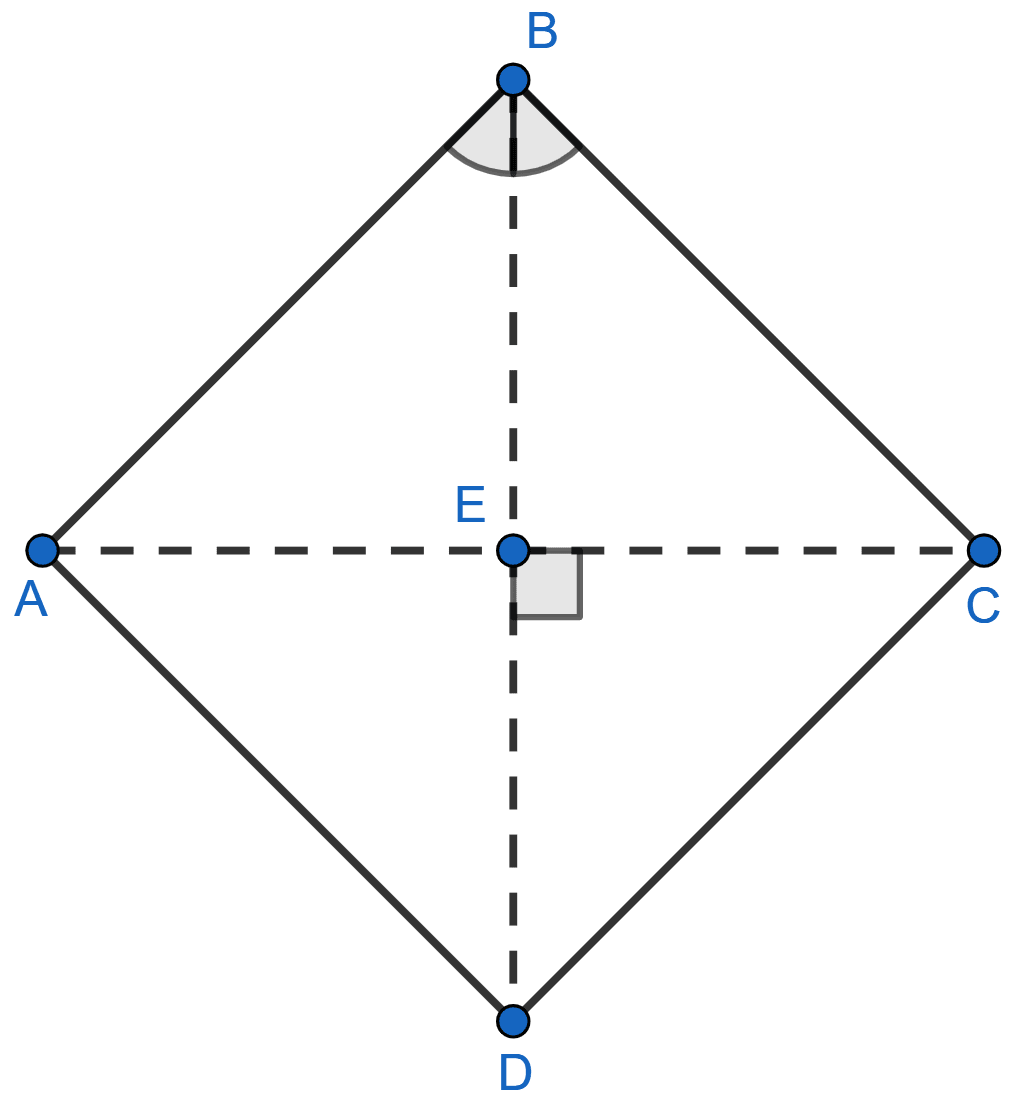
In rhombus,
Diagonals bisect each other at right angles.
Hence, the locus of point in a rhombus ABCD which is equidistant from B and D is diagonal AC.
Answered By
3 Likes
Related Questions
Describe the locus of vertices of all isosceles triangles having a common base.
Describe the locus of a point P, so that :
AB2 = AP2 + BP2,
where A and B are two fixed points.
Describe :
(i) The locus of points at distances less than 3 cm from a given point.
(ii) The locus of points at distances greater than 4 cm from a given point.
(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
(iv) The locus of points at distances greater than or equal to 35 mm from a given point.
(v) The locus of the center of a given circle which rolls around the outside of a second circle and is always touching it.
(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle.
(vii) The locus of the mid-points of all chords parallel to a given chord of a circle.
(viii) The locus of points within a circle that are equidistant from the end points of a given chord.
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
