Mathematics
Describe the locus of vertices of all isosceles triangles having a common base.
Locus
15 Likes
Answer
We know that,
The locus of point equidistant from two points is the perpendicular bisector of the line joining those points.
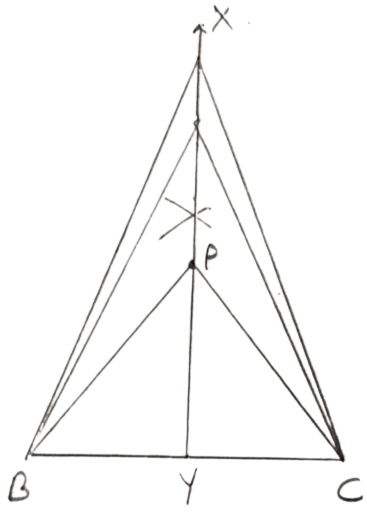
Steps of construction :
Draw a line segment BC (common base)
Draw XY, perpendicular bisector of BC.
Mark point P on XY.
So, PB = PC as P lies on perpendicular bisector of BC.
Hence, the locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
Answered By
10 Likes
Related Questions
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of the centers of all circles passing through two fixed points.
Describe the locus of a point P, so that :
AB2 = AP2 + BP2,
where A and B are two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC.
(ii) B and D.