Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.

Steps of construction :

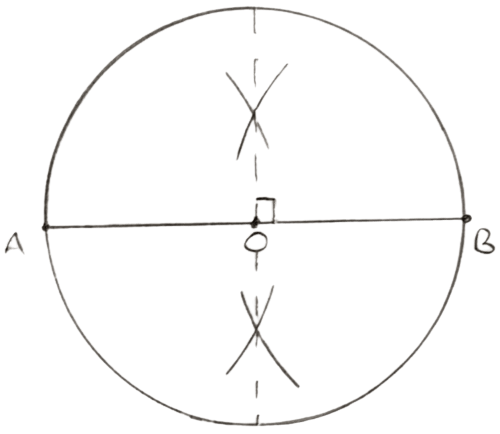
1. Draw a circle with O as center.

2. Mark two points A and B. Join AB.

3. Draw perpendicular bisector of AB. It should pass through center of the circle.

Since, O lies on perpendicular bisector of AB so OA = OB.

Hence, the locus of points inside the circle which are equidistant from the two fixed points on the circumference of a circle will be the diameter which is the perpendicular bisector of the chord joining the two fixed points on the circle.