Mathematics
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
Circles
46 Likes
Answer
Let there be two circles with center A and B and radius 12 and 4 cm respectively.
From figure,
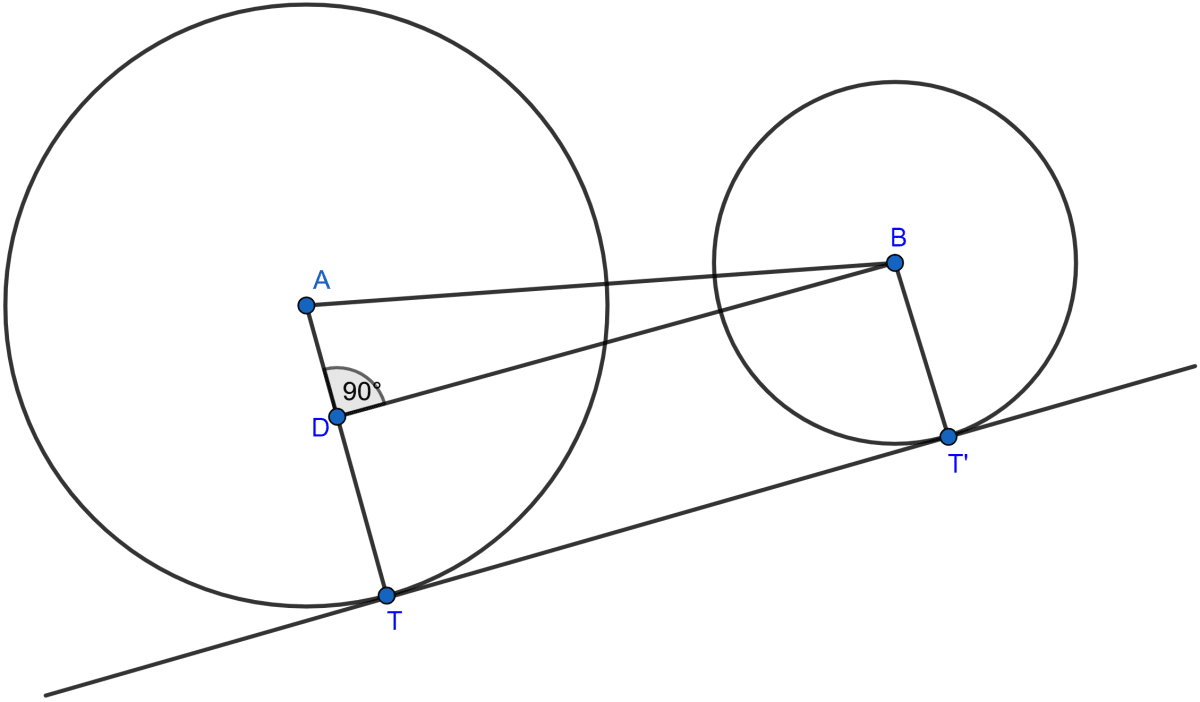
TT' is the common tangent.
DT = BT' = 4 cm.
DB = TT' = 15 cm.
In right angled triangle ADB
AD = AT - DT = 12 - 4 = 8 cm
Hence, the distance between two centres = 17 cm.
Answered By
27 Likes
Related Questions
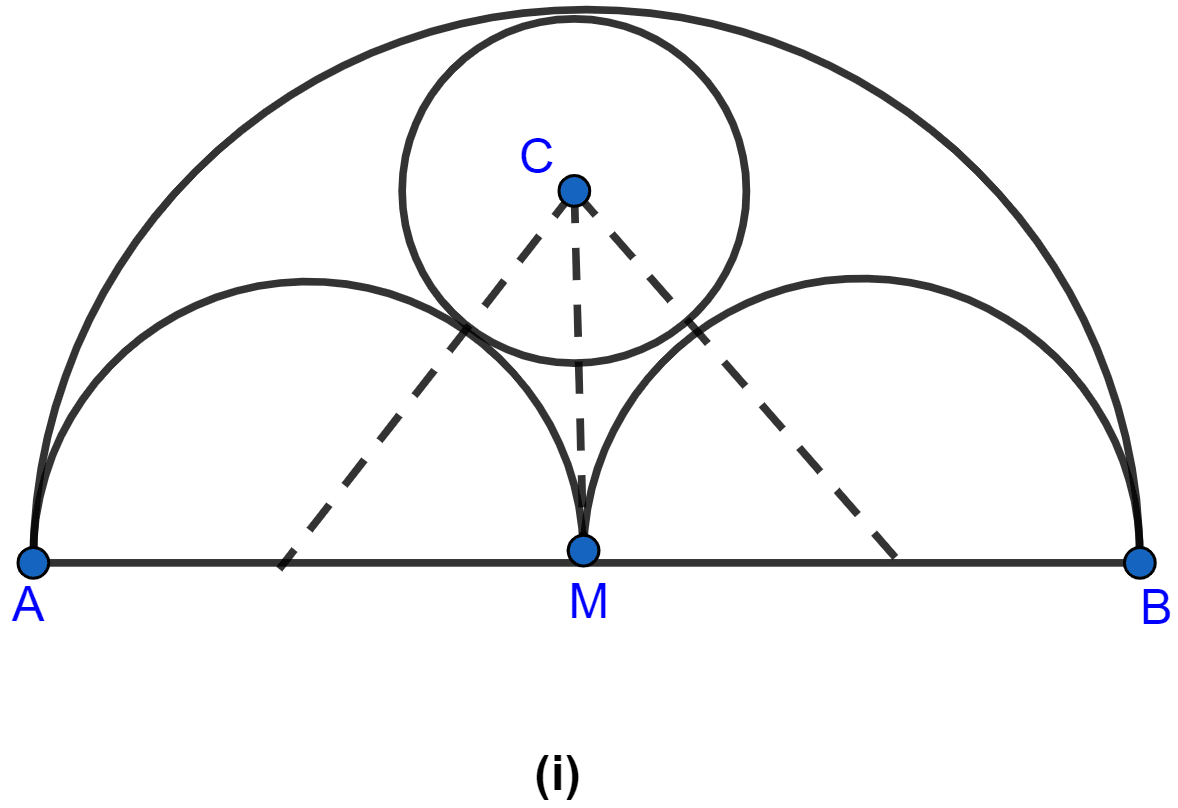
In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semicircles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semicircles as shown, find its radius.
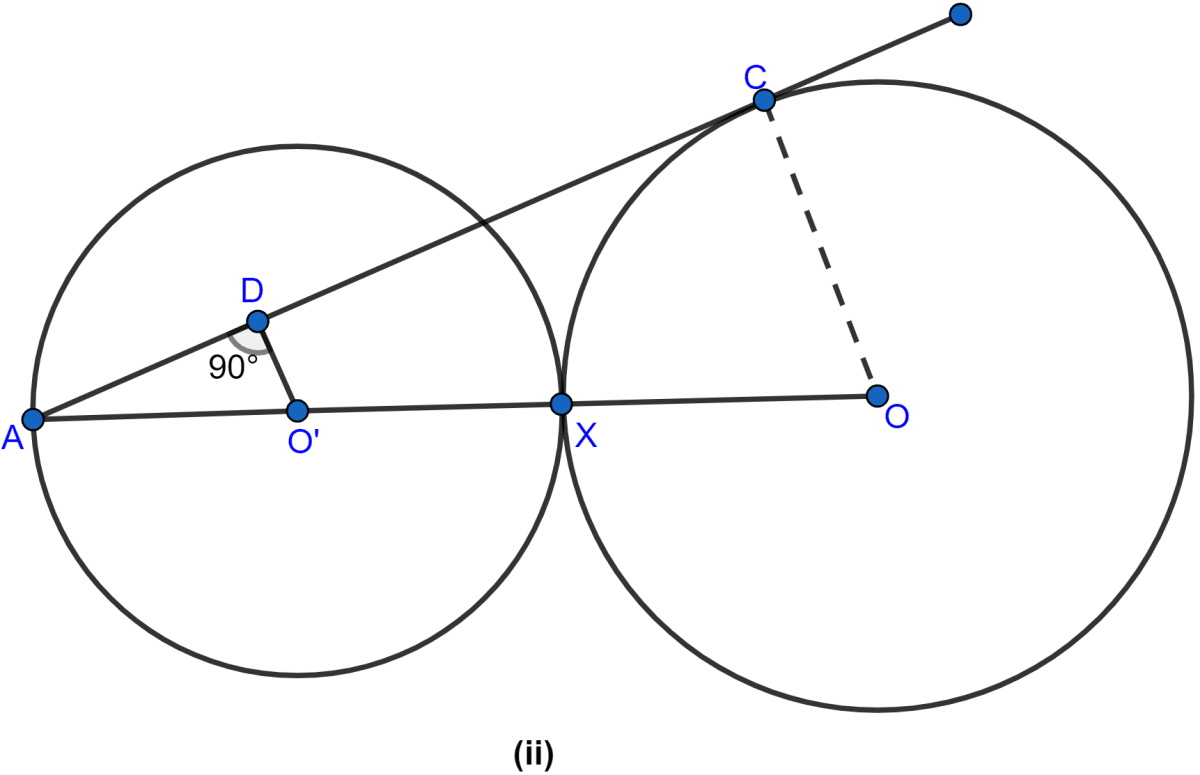
In the figure (ii) given below, equal circles with centres O and O' touch each other at X. OO' is produced to meet a circle O' at A. AC is tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of
(i)
(ii)
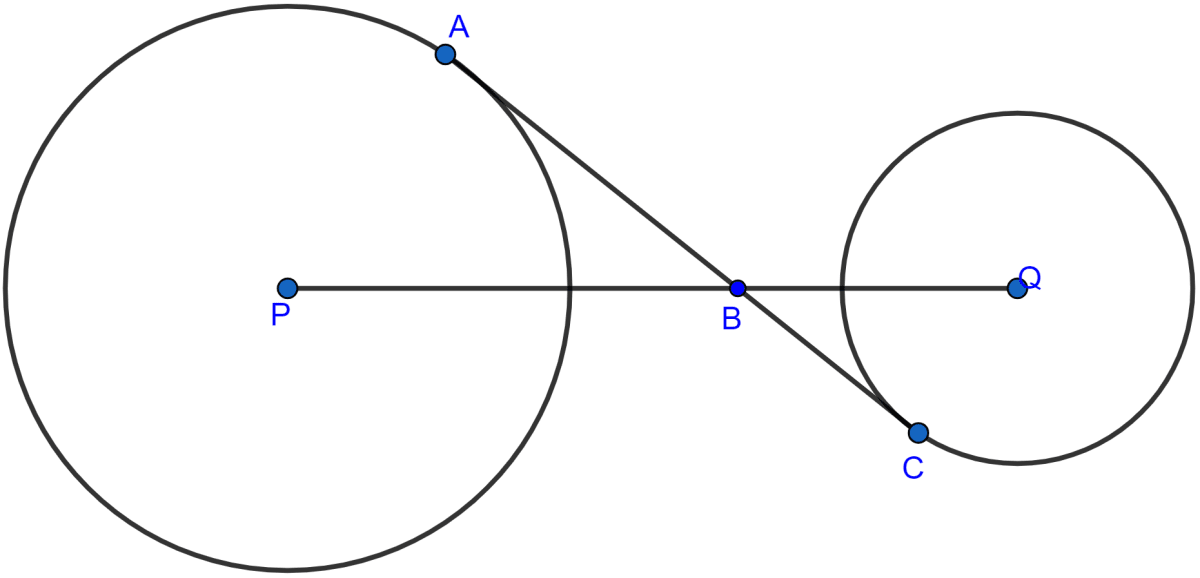
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.