Mathematics
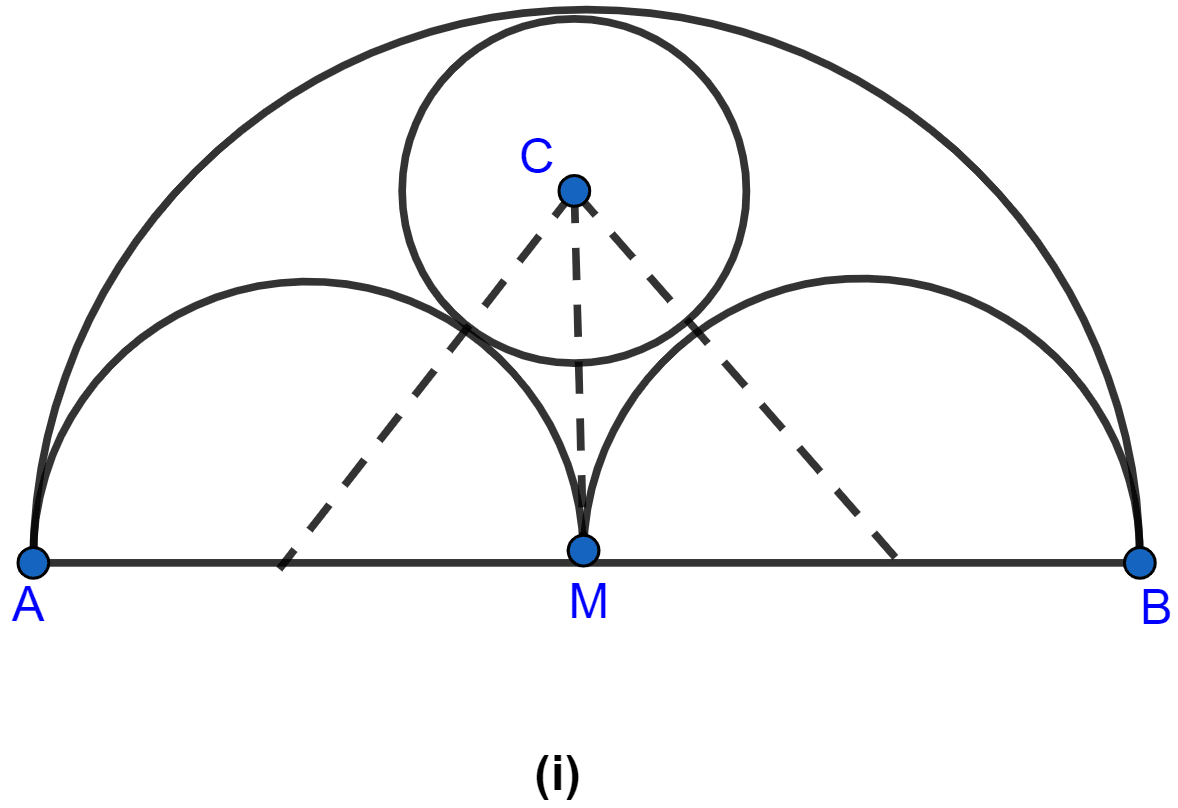
In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semicircles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semicircles as shown, find its radius.
Circles
41 Likes
Answer
Let x be the radius of the circle with centre C.
Since M is the mid-point of AB hence, AM = MB = 4 cm.
Two semicircles are thus drawn on AB with diameters as AM and MB.
Since radius = .
Hence, radius of both the semicircles with diameters AM and MB = 2 cm.
From figure,
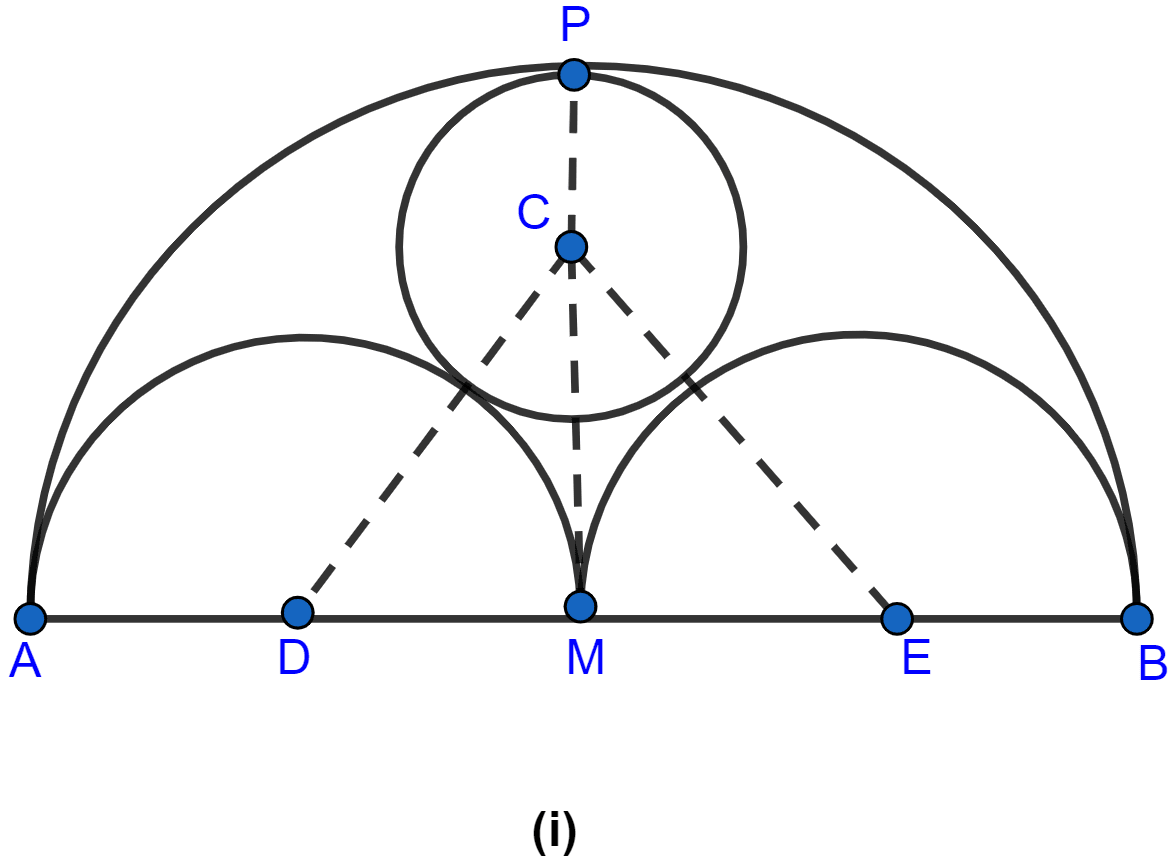
CM = MP - PC = (4 - x) cm.
In right angled triangle CMD,
Hence, the radius of small circle = cm.
Answered By
22 Likes
Related Questions
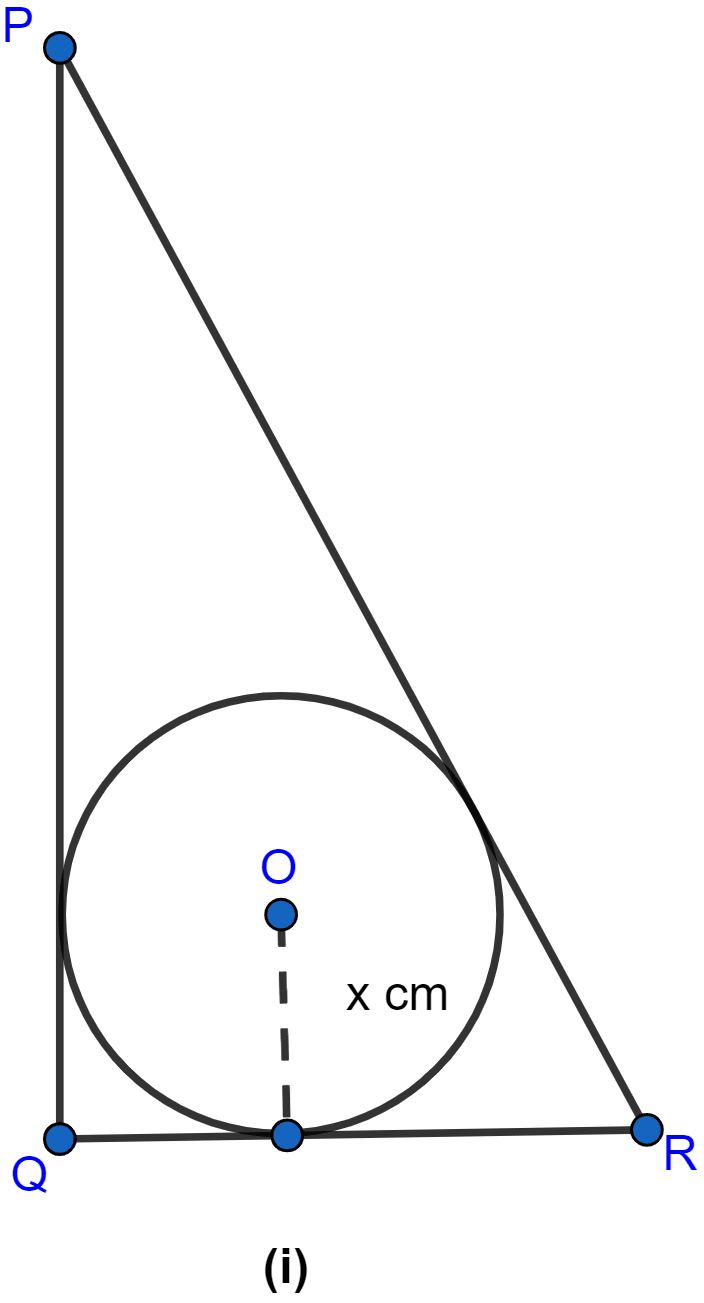
In the figure (i) given below, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle of △PQR.
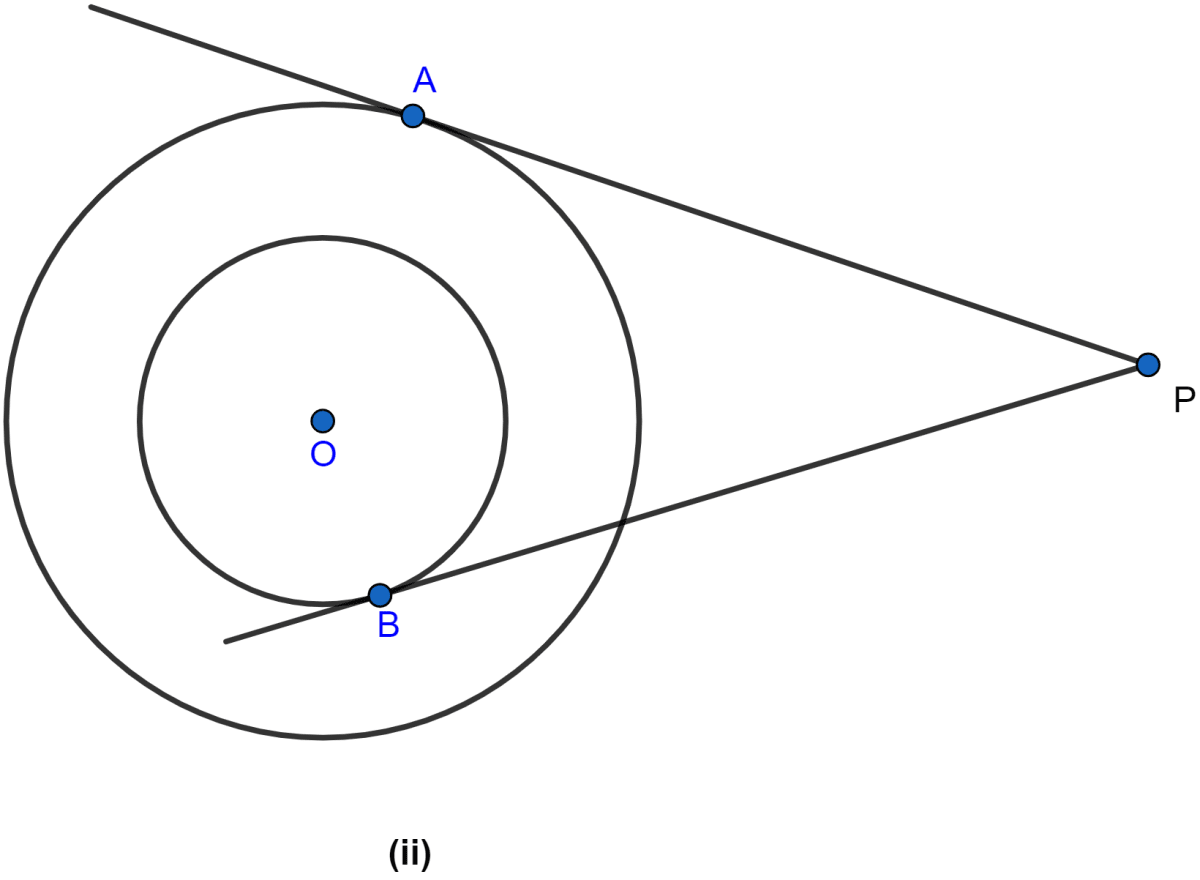
In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12 cm, find BP.
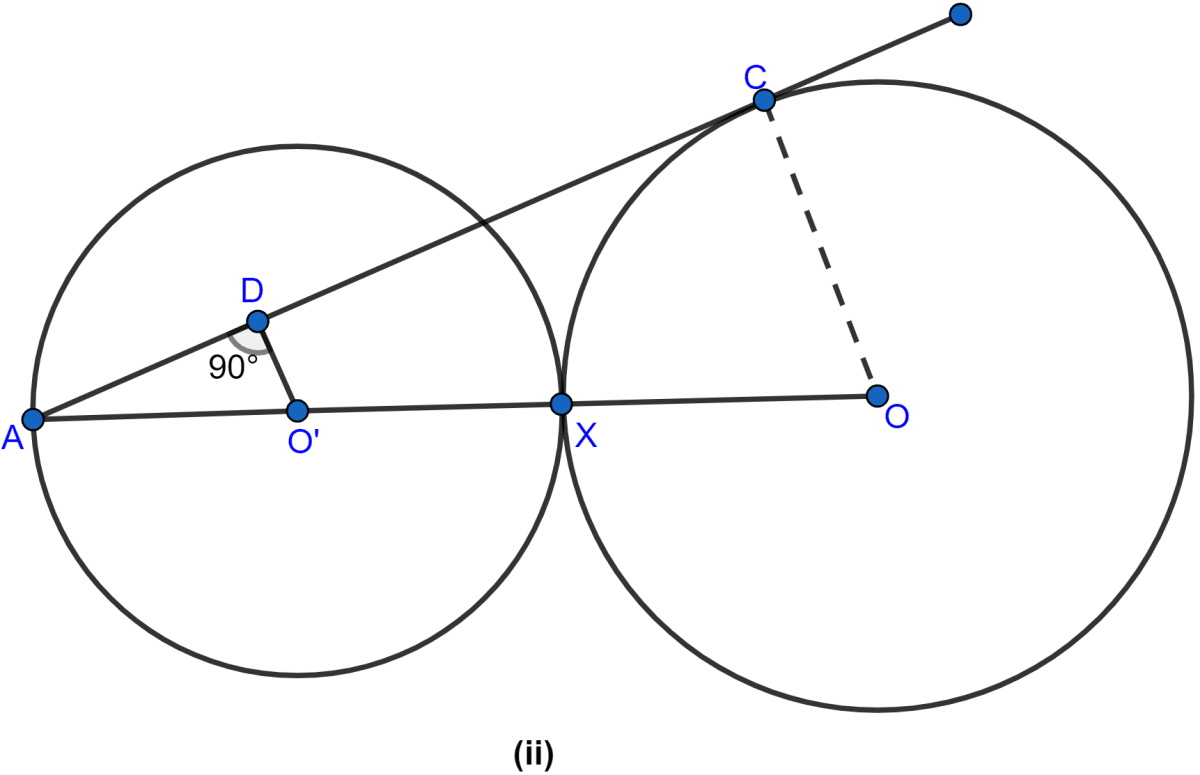
In the figure (ii) given below, equal circles with centres O and O' touch each other at X. OO' is produced to meet a circle O' at A. AC is tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of
(i)
(ii)
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.