Mathematics
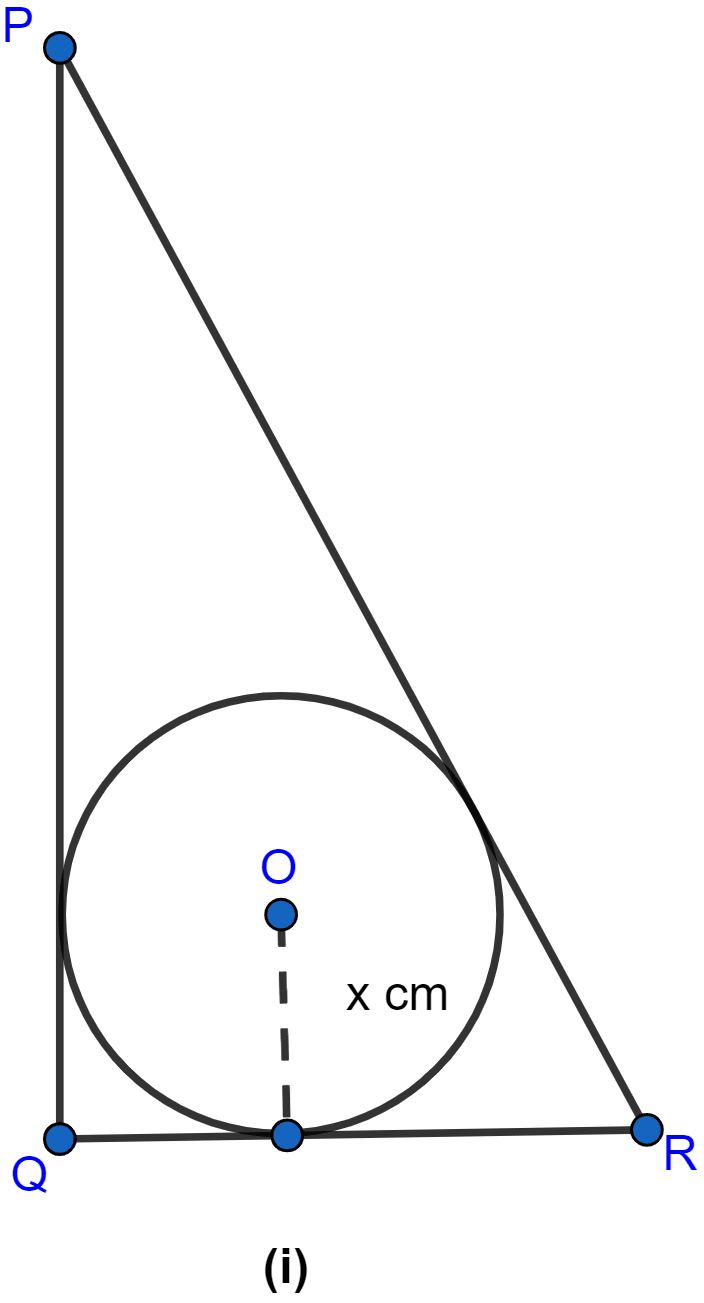
In the figure (i) given below, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle of △PQR.
Circles
39 Likes
Answer
Let the sides of triangle PQ, QR and PR meet the circle at L, M and N respectively.
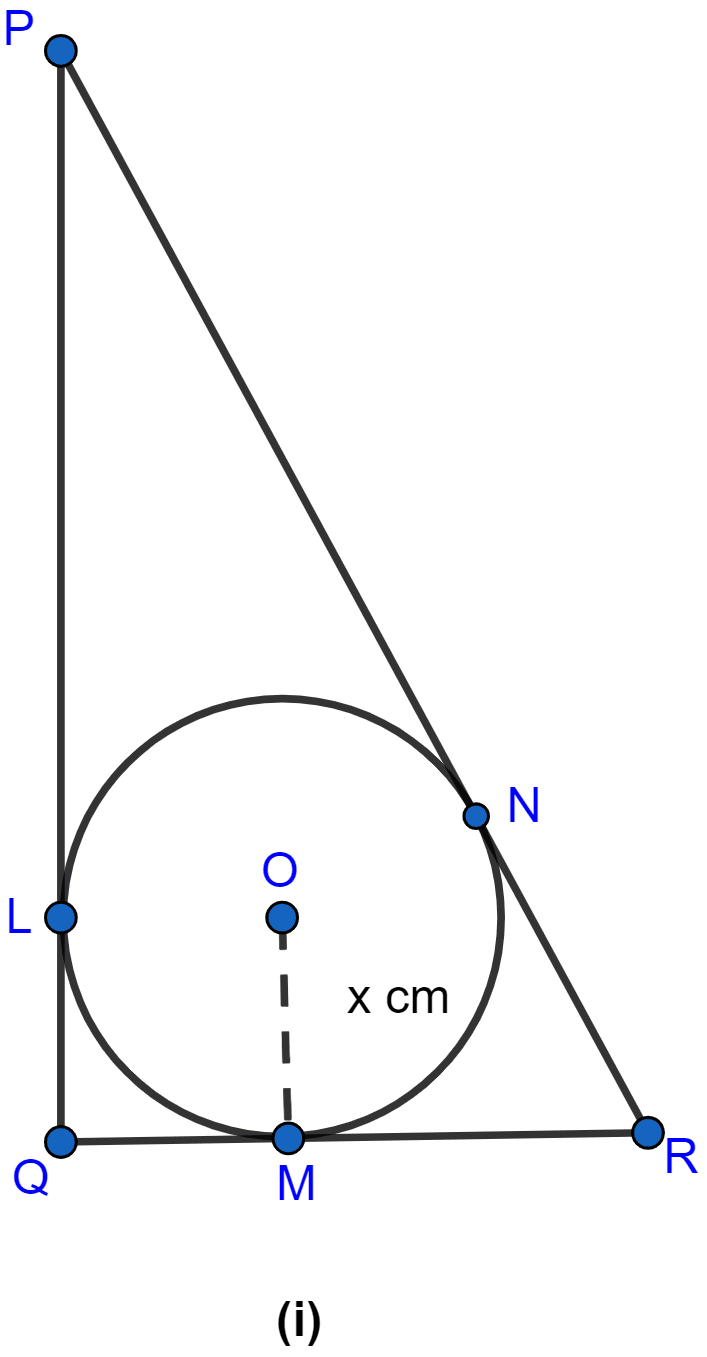
In right-angled triangle PQR
From figure,
RM = RN = (∵ tangents drawn from a common external point to a circle are equal.)
RM = RQ - QM = (7 - x) cm.
PL = PN = (∵ tangents drawn from a common external point to a circle are equal.)
PL = PQ - QL = (24 - x) cm.
We can see,
PR = PN + RN = PL + RM.
⇒ 25 = 24 - x + 7 - x
⇒ 25 = 31 - 2x
⇒ 2x = 31 - 25
⇒ 2x = 6
⇒ x = 3.
Hence, the radius of the inscribed circle is 3 cm.
Answered By
25 Likes
Related Questions
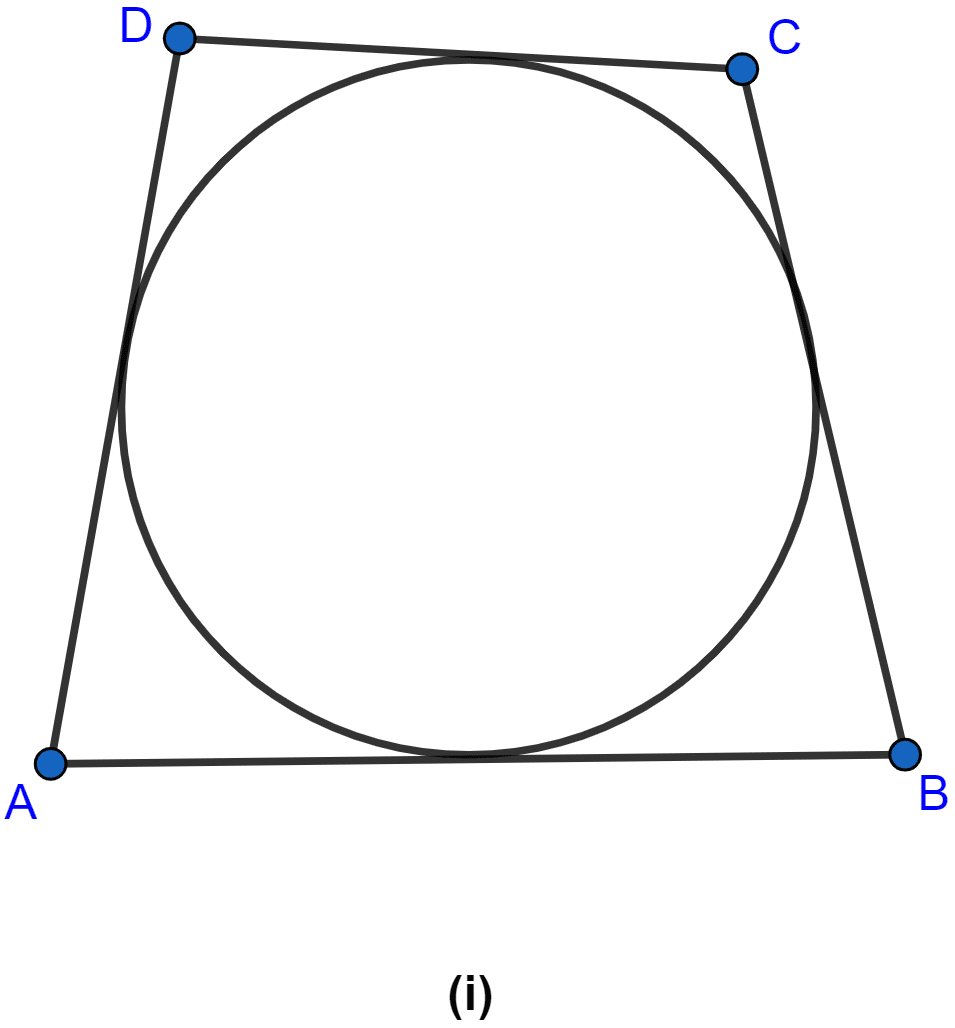
In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
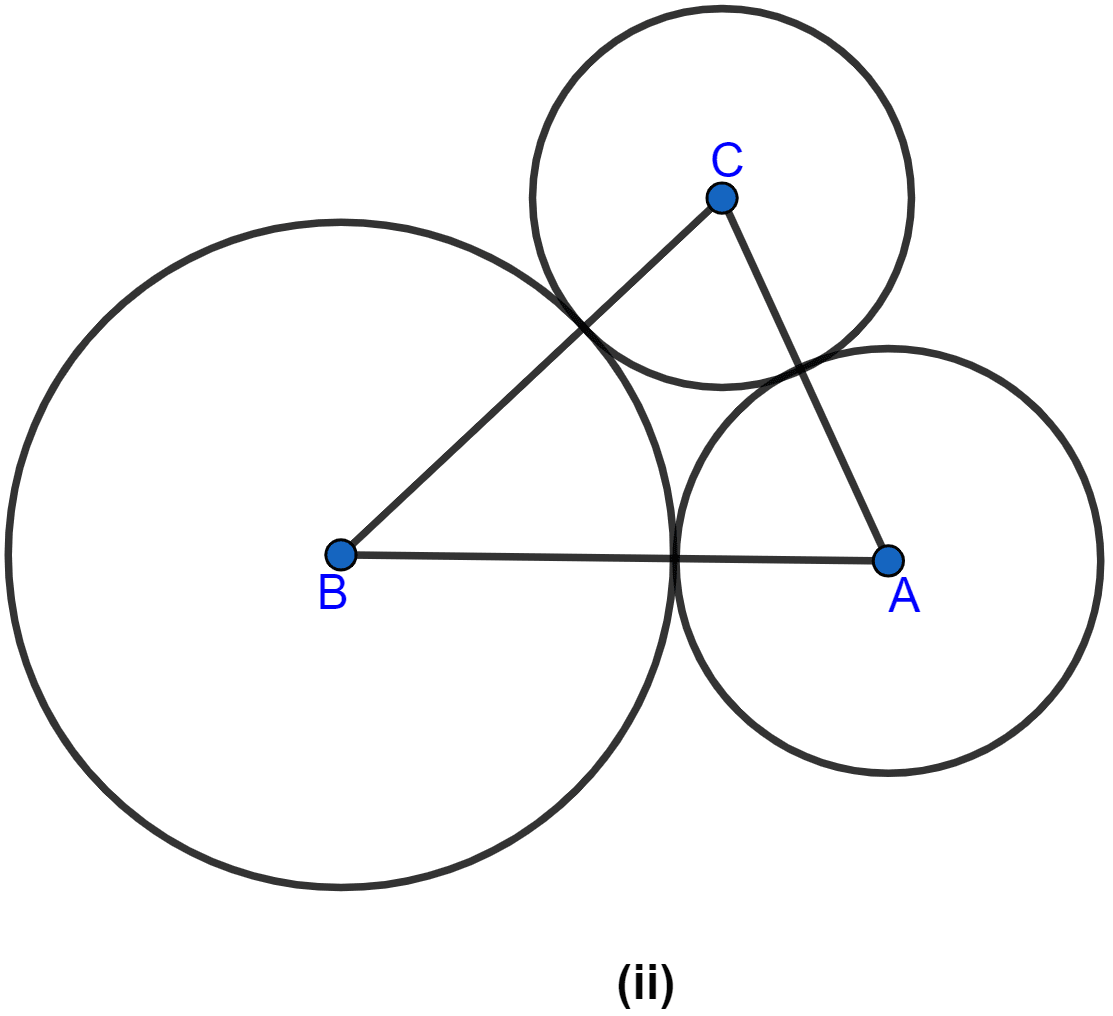
In the figure (ii) given below, ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles.
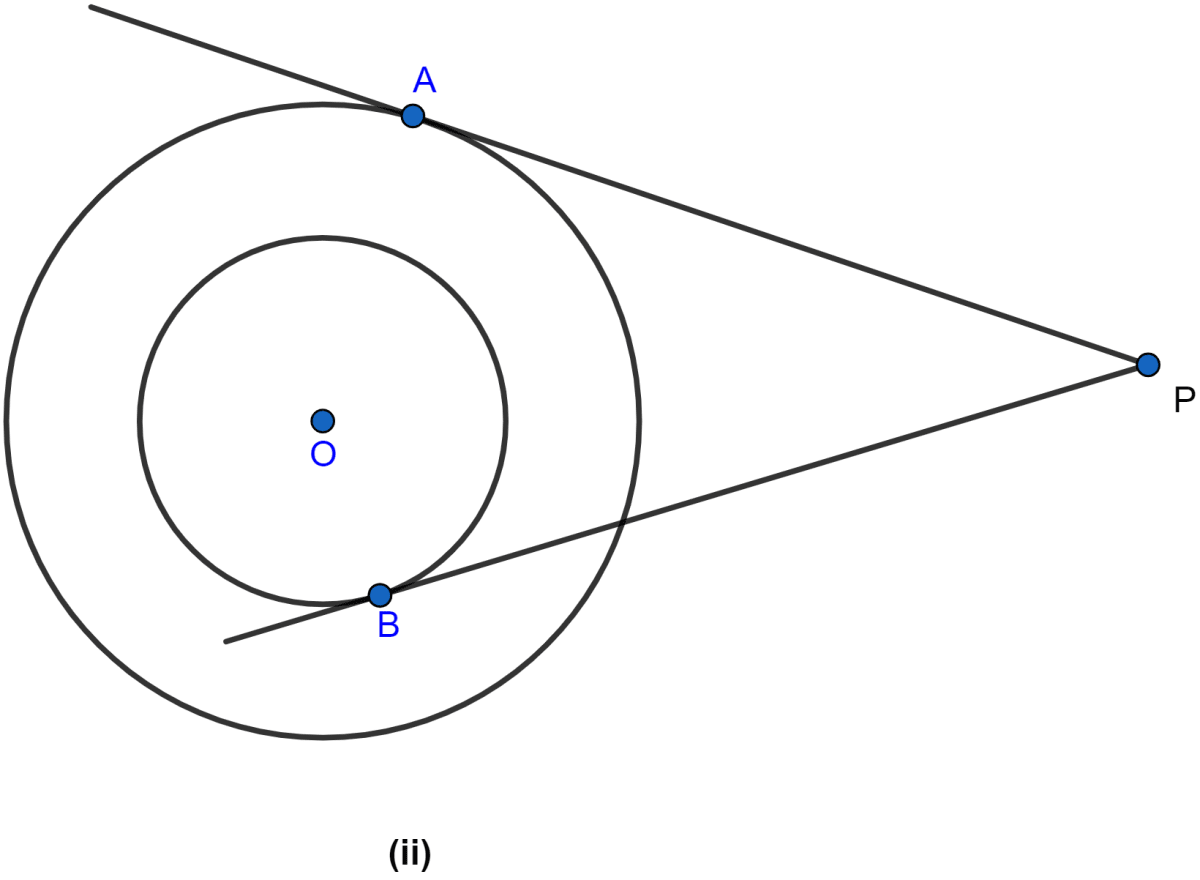
In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12 cm, find BP.
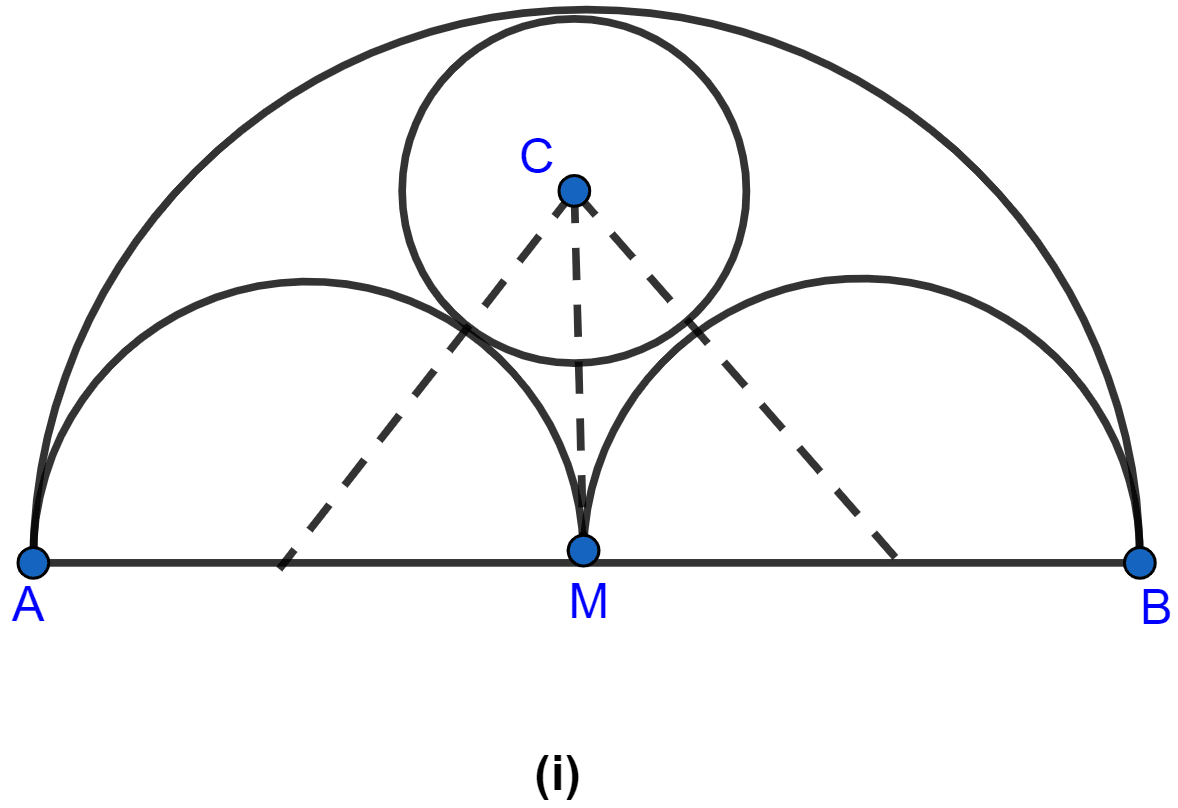
In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semicircles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semicircles as shown, find its radius.