Mathematics
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
Circles
26 Likes
Answer
Let there be two circles with centre A and B with radius 8 cm and 3 cm respectively.
Let TT' be the length of common tangent.
From figure,

DT = BT' = 3cm.
AD = AT - DT = 8 - 3 = 5 cm.
In right angled triangle ADB
Since, TDBT' is a rectangle,
So, TT' = DB = 12 cm.
Hence, the length of direct common tangent is 12 cm.
Answered By
14 Likes
Related Questions
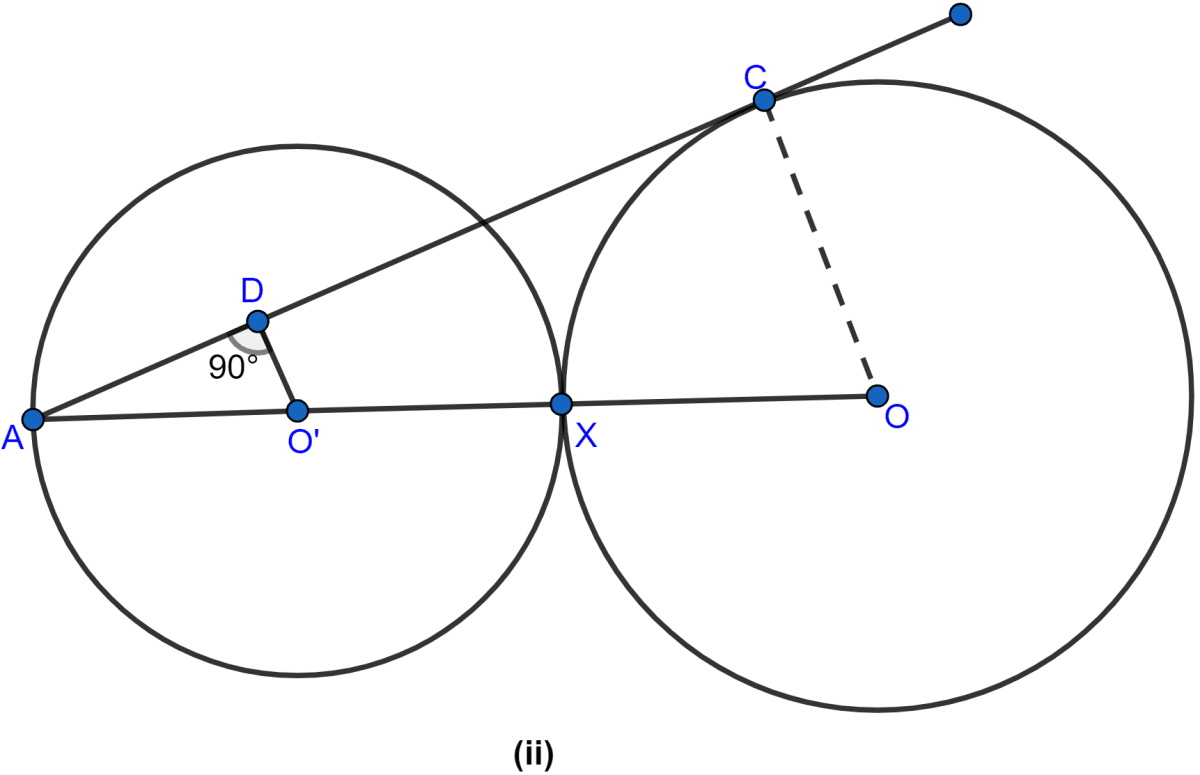
In the figure (ii) given below, equal circles with centres O and O' touch each other at X. OO' is produced to meet a circle O' at A. AC is tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of
(i)
(ii)
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
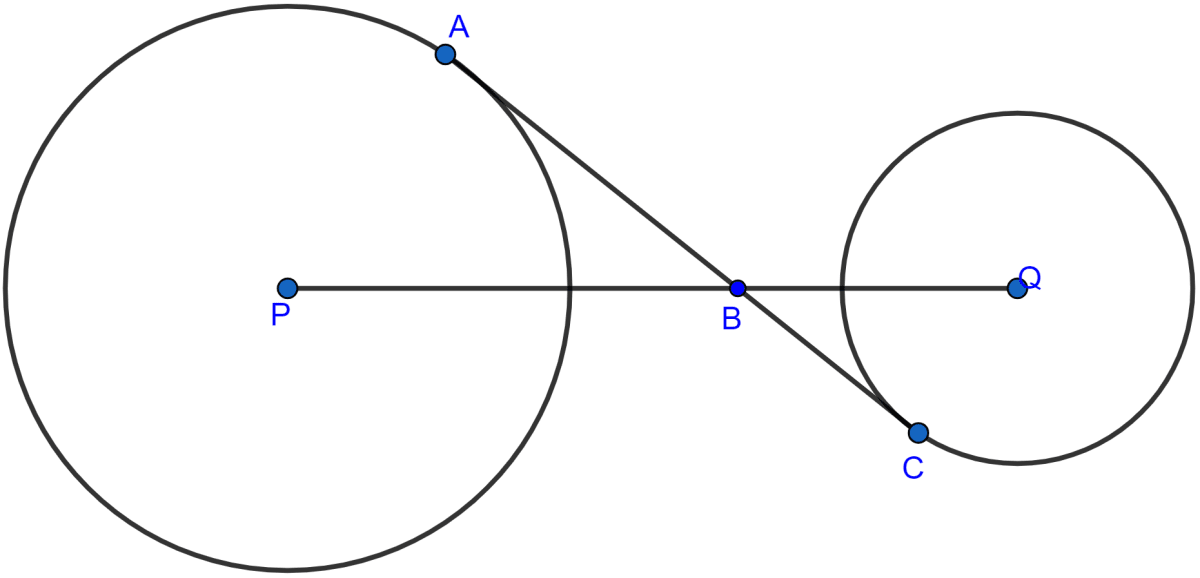
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.