Mathematics
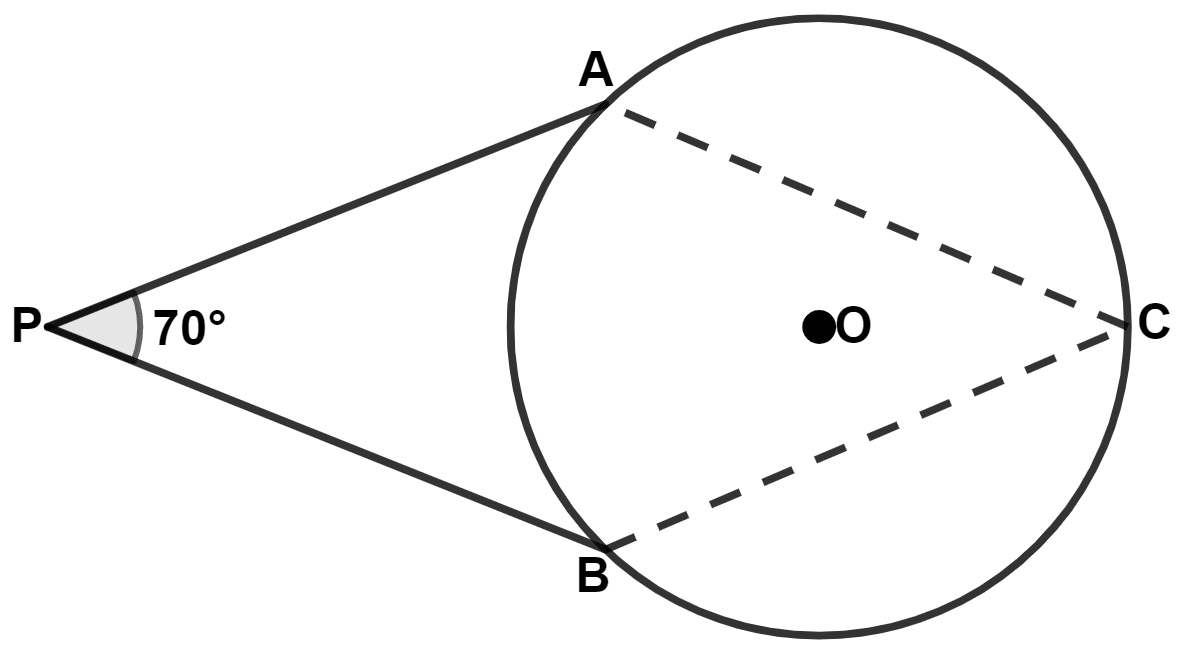
PA and PB are tangents to a circle with center O. If angle BPA = 70°, the angle ACB is :
70°
105°
140°
55°
Circles
13 Likes
Answer
Join OA and OB.
We know that,
Tangent at any point of a circle and the radius through this point are perpendicular to each other.
∴ ∠OAP = 90° and ∠OBP = 90°
In quadrilateral OAPB,
⇒ ∠OAP + ∠APB + ∠PBO + ∠BOA = 360°
⇒ 90° + 70° + 90° + ∠BOA = 360°
⇒ ∠BOA + 250° = 360°
⇒ ∠BOA = 360° - 250° = 110°.
We know that,
The angle which an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = ∠AOB
⇒ ∠ACB = = 55°.
Hence, Option 4 is the correct option.
Answered By
8 Likes
Related Questions
A, B and C are three circles which touch each other as shown. Using the information, given in the diagram, we find the length AB as :
6 cm
17 cm
(289 - 9 - 2) cm
11 cm

BC is a tangent to the circle with center O. OD is radius of the circle. If ∠DOC = 100°, ∠B is equal to :
50°
60°
40°
70°
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre.
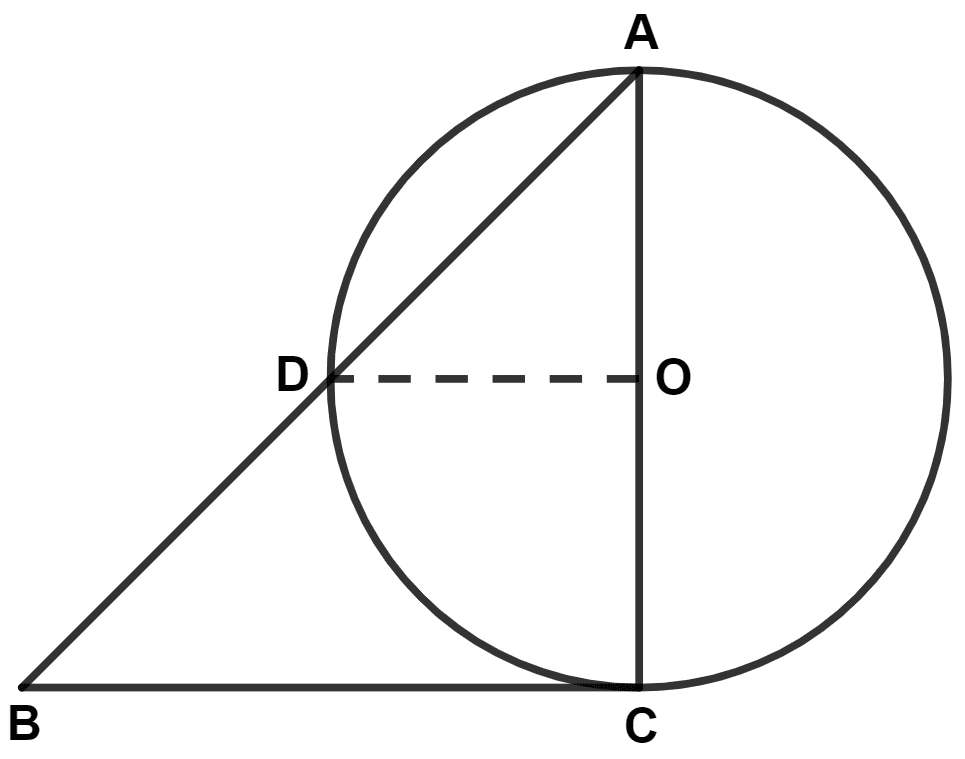
In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.