Mathematics
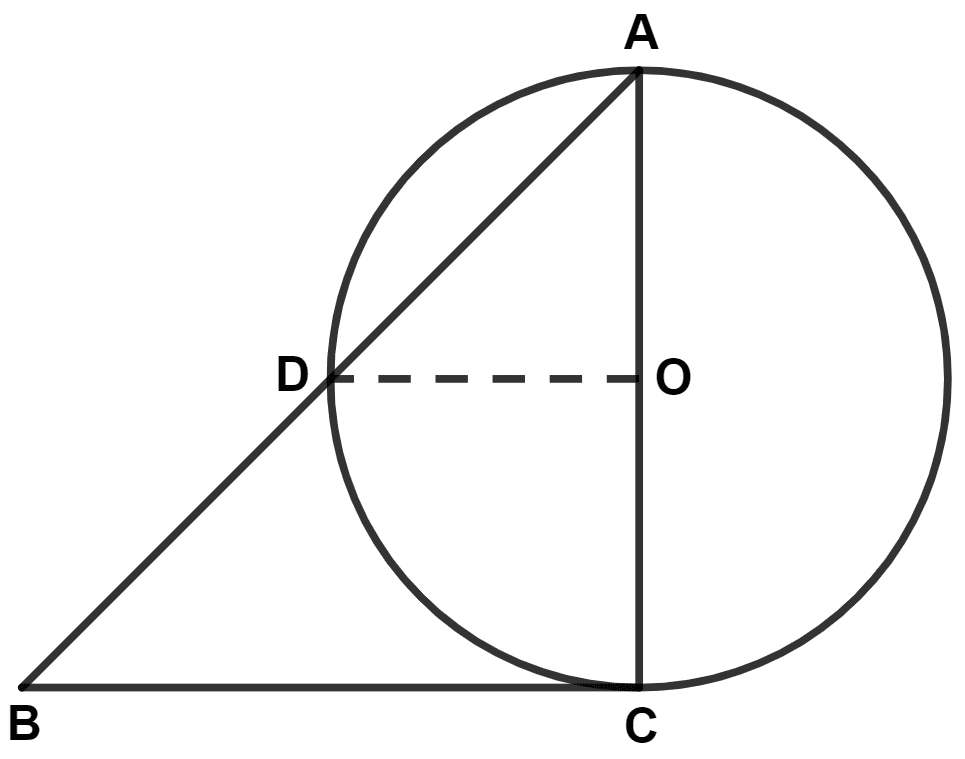
BC is a tangent to the circle with center O. OD is radius of the circle. If ∠DOC = 100°, ∠B is equal to :
50°
60°
40°
70°
Circles
17 Likes
Answer
From figure,
OD = OA (Radius of same circle)
In △OAD,
∠ODA = ∠OAD = x (let) (As angles opposite to equal sides are equal)
Since, exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ ∠DOC = ∠ODA + ∠OAD
⇒ 100° = 2x
⇒ x =
⇒ x = 50°.
⇒ ∠OAD = 50°.
We know that,
Tangent at any point of a circle and the radius through this point are perpendicular to each other.
∴ ∠BCA = 90°.
In △ABC,
By angle sum property of triangle,
⇒ ∠ABC + ∠BCA + ∠CAB = 180°
⇒ ∠ABC + ∠BCA + ∠OAD = 180° [∵ From figure, ∠CAB = ∠OAD]
⇒ ∠ABC + 90° + 50° = 180°
⇒ ∠ABC + 140° = 180°
⇒ ∠ABC = 180° - 140° = 40°.
Hence, Option 3 is the correct option.
Answered By
10 Likes
Related Questions
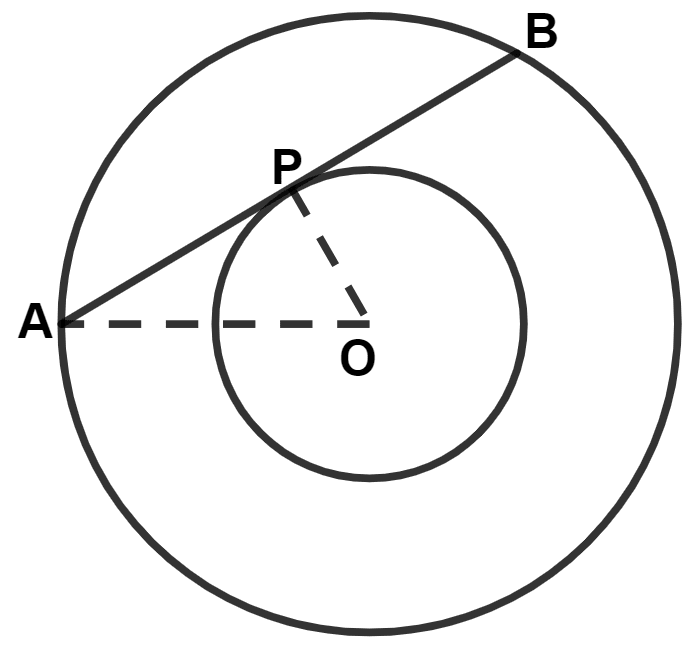
In the given figure, APB is tangent to the inner circle and also a chord of outer circle. Both the circles are concentric. If OA = 10 cm and OP = 6 cm, the length of AB is :
16 cm
10 cm
14 cm
20 cm
A, B and C are three circles which touch each other as shown. Using the information, given in the diagram, we find the length AB as :
6 cm
17 cm
(289 - 9 - 2) cm
11 cm

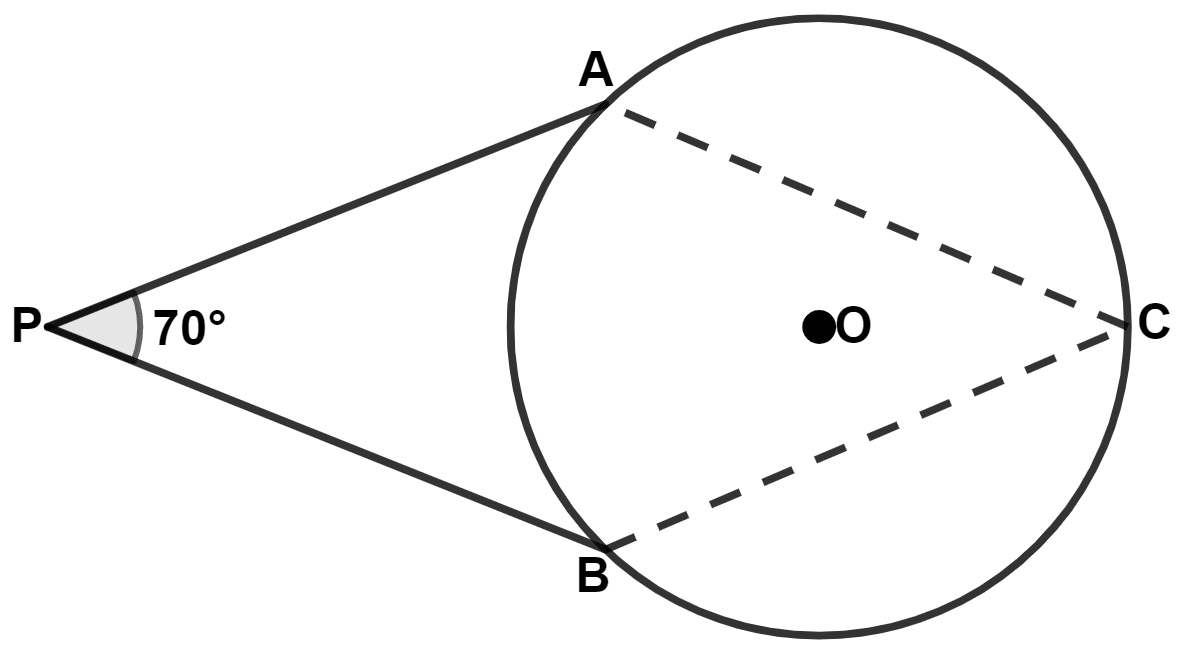
PA and PB are tangents to a circle with center O. If angle BPA = 70°, the angle ACB is :
70°
105°
140°
55°
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre.