Mathematics
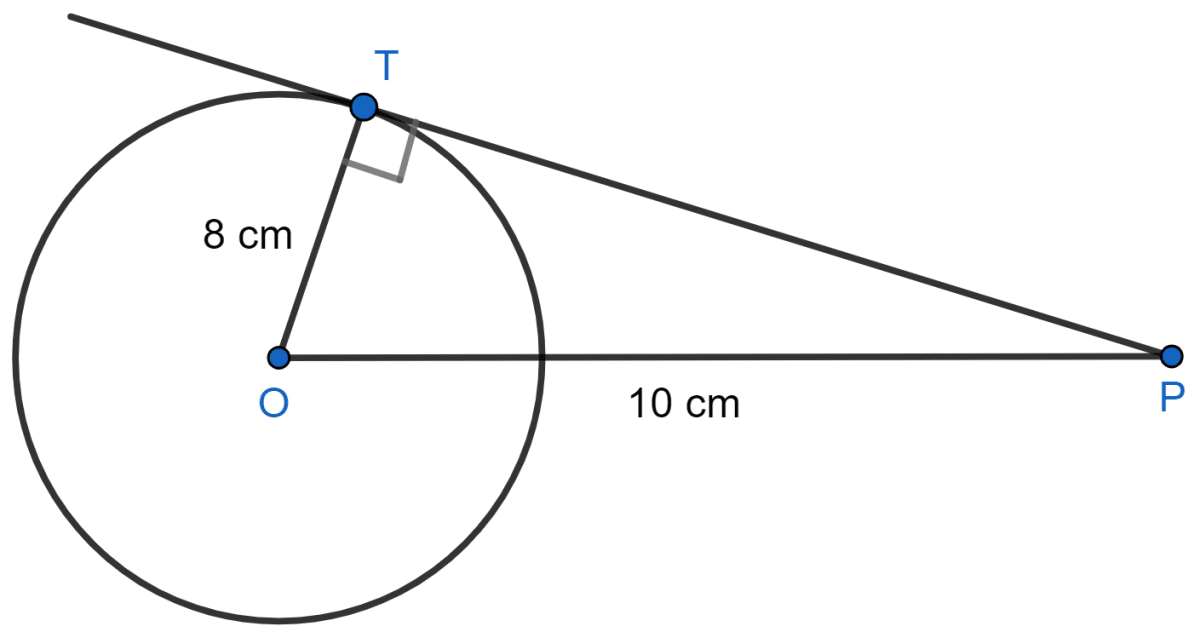
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre.
Circles
7 Likes
Answer
Let a circle be with centre O and radius 8 cm.
Let P be an external point from where a tangent is drawn to meet the circle at T.
∴ OP = 10 cm and OT = 8 cm
We know that,
The tangent at any point of a circle and the radius through this point are perpendicular to each other.
In right ∆OTP, we have
⇒ OP2 = OT2 + PT2 [By Pythagoras Theorem]
⇒ 102 = 82 + PT2
⇒ PT2 = 100 - 64 = 36
⇒ PT = 6 cm.
Hence, the length of tangent = 6 cm.
Answered By
3 Likes
Related Questions
BC is a tangent to the circle with center O. OD is radius of the circle. If ∠DOC = 100°, ∠B is equal to :
50°
60°
40°
70°
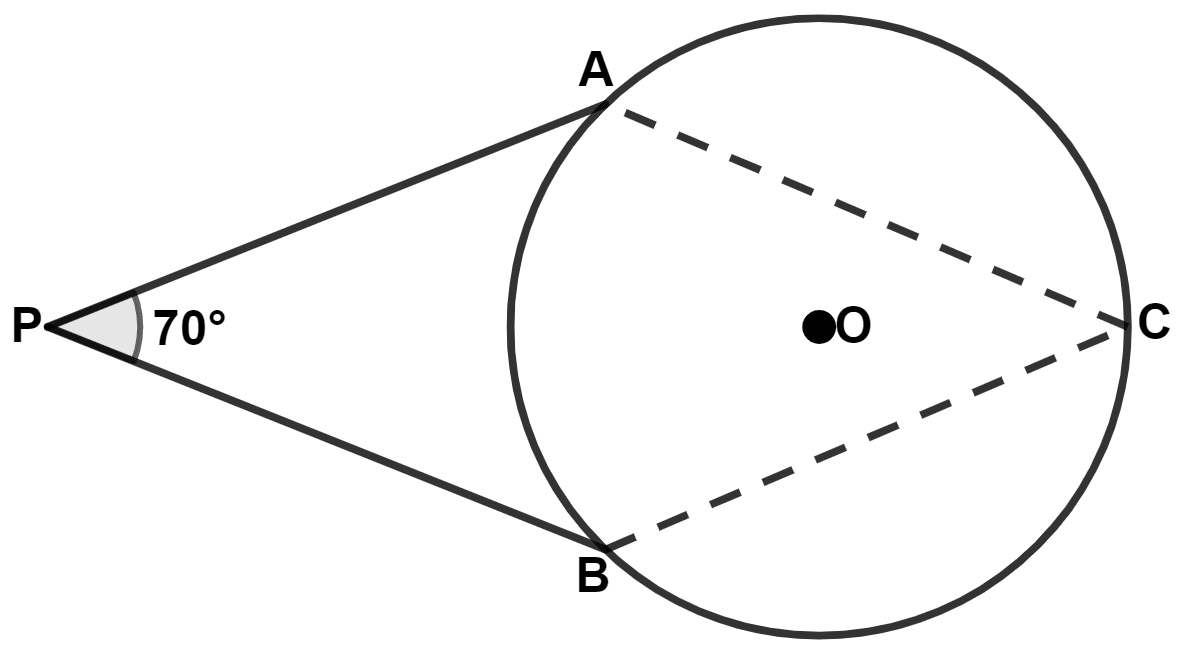
PA and PB are tangents to a circle with center O. If angle BPA = 70°, the angle ACB is :
70°
105°
140°
55°
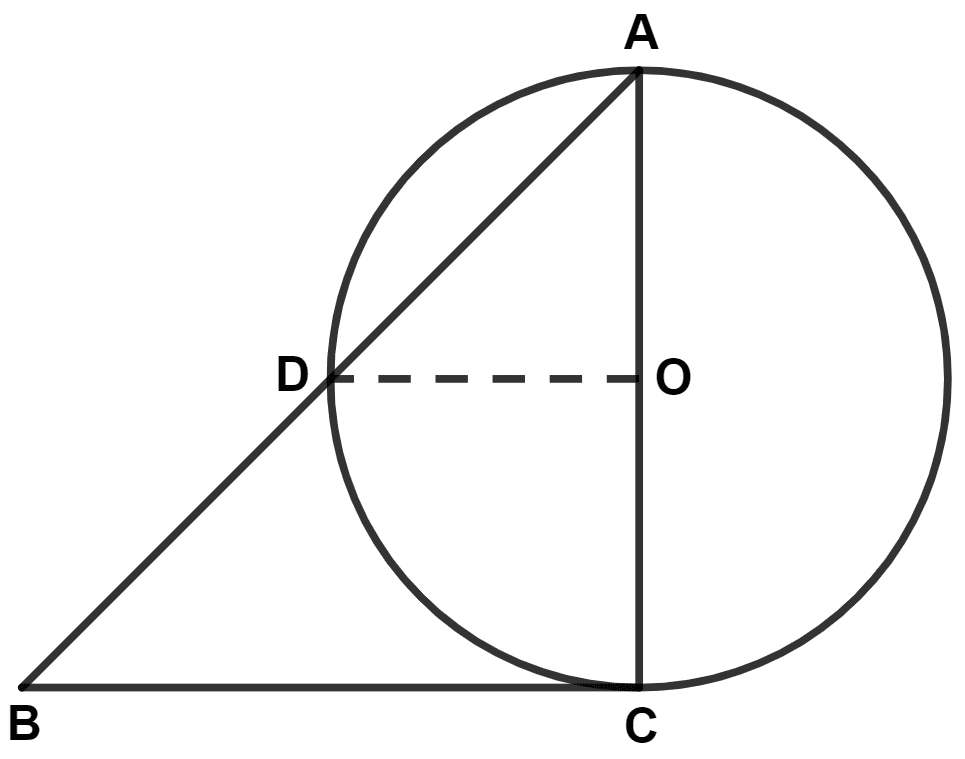
In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
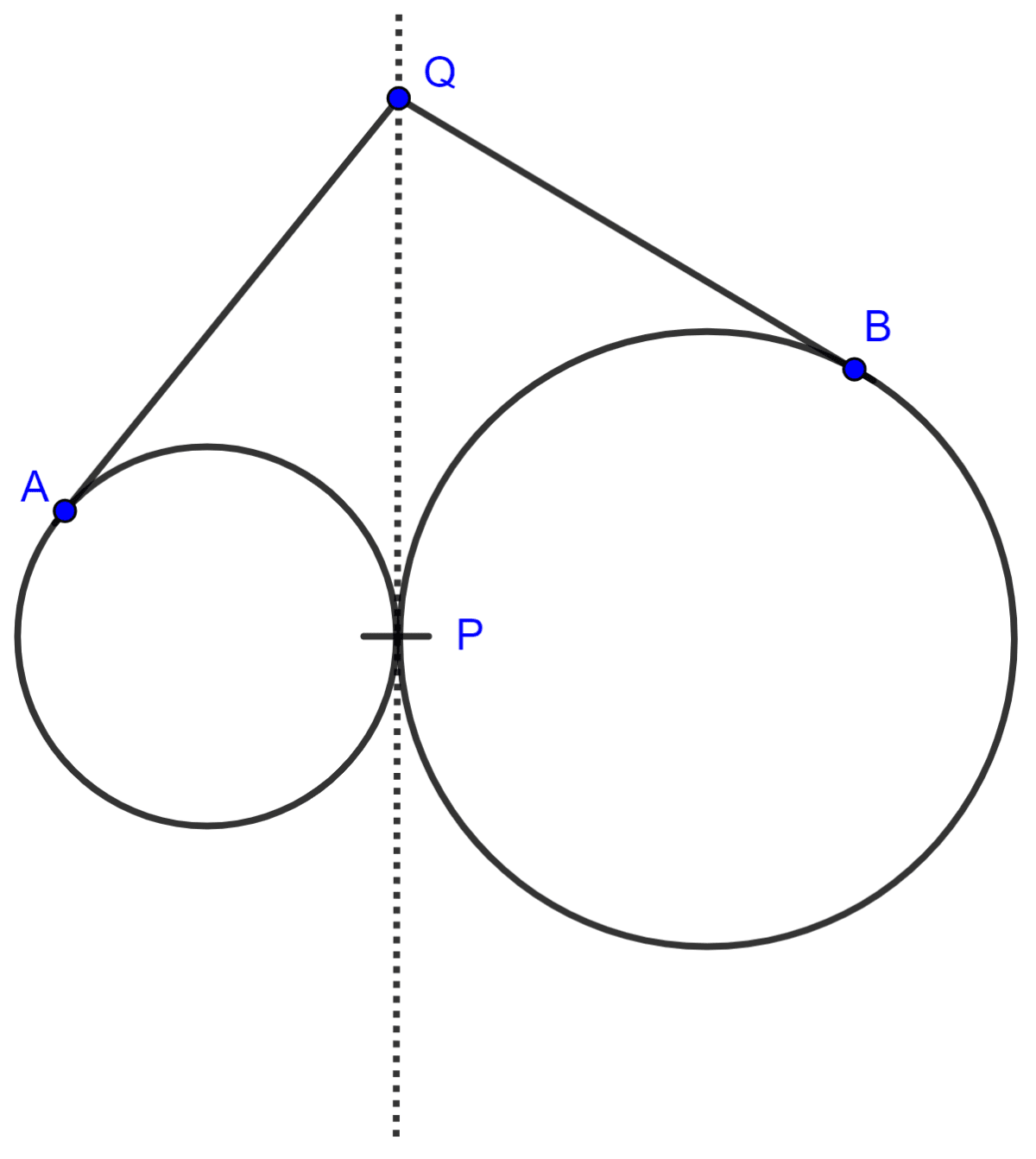
Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.