Mathematics
Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
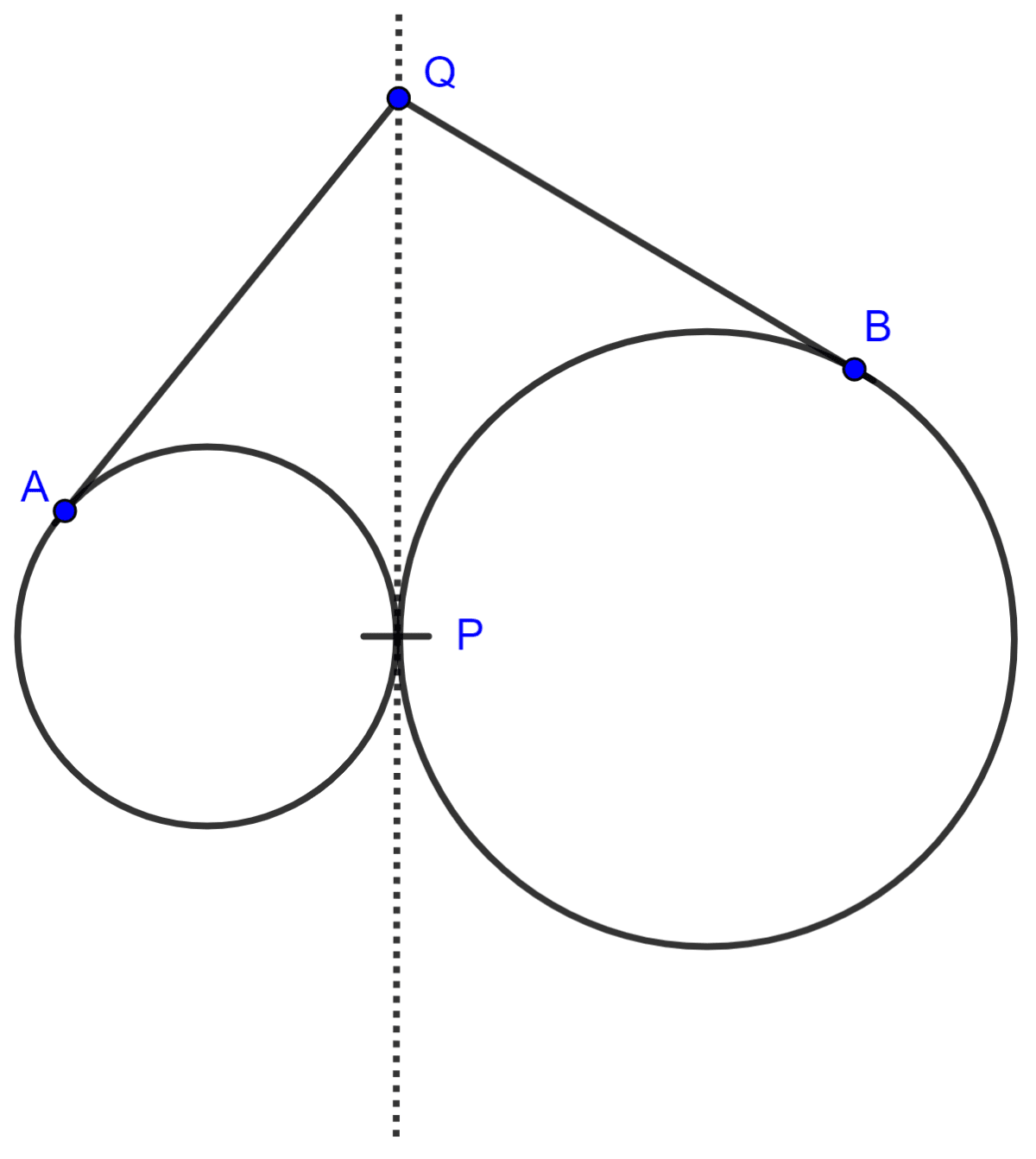
Circles
12 Likes
Answer
We know that,
If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.
From figure,
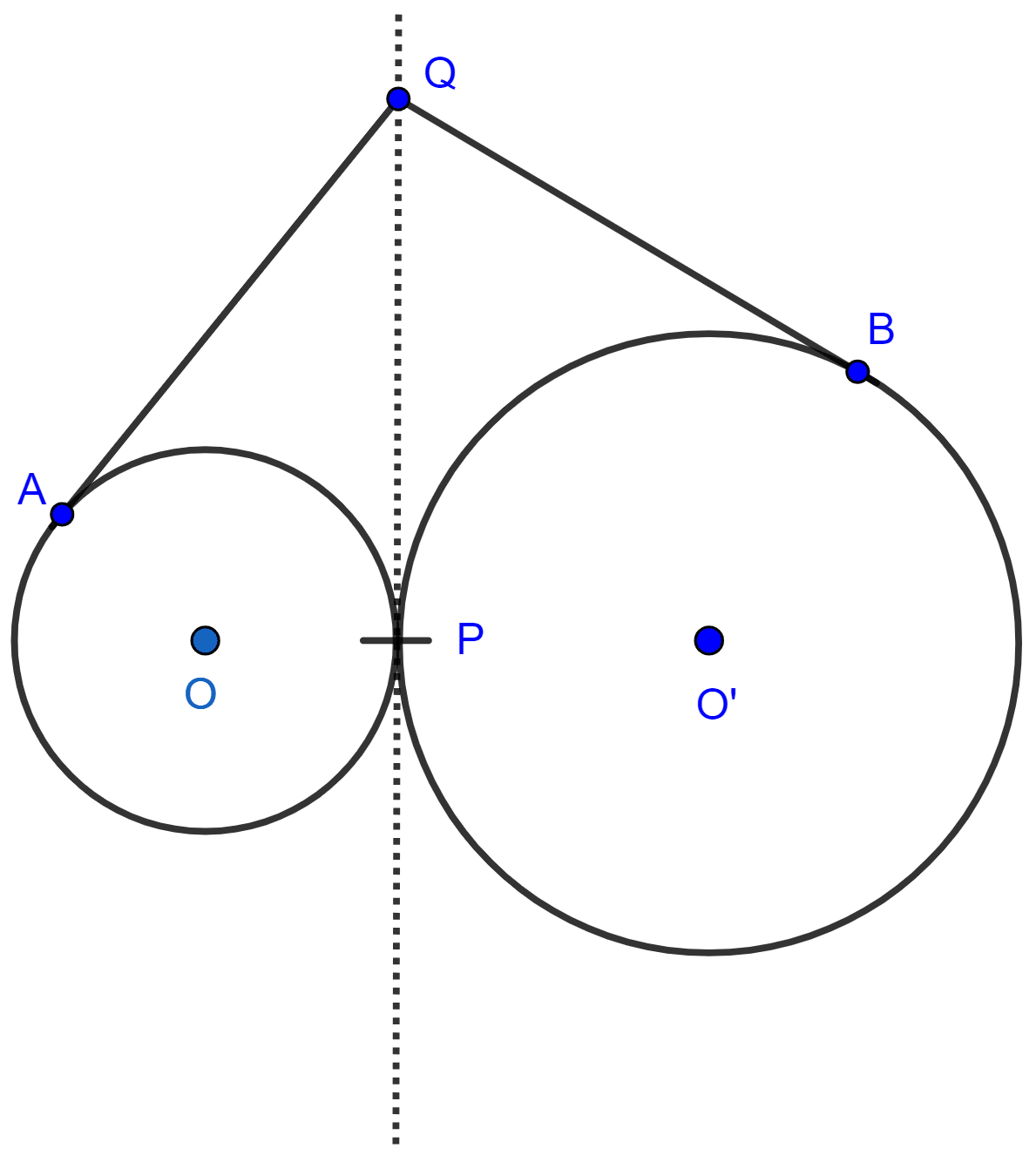
Q is the point from which, QA and QP are two tangents to the circle with centre O
So, QA = QP ……….(1)
Similarly, from point Q, QB and QP are two tangents to the circle with centre O’
So, QB = QP ……….(2)
From (1) and (2), we have
QA = QB
Hence, proved that the tangents are equal.
Answered By
4 Likes
Related Questions
The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre.
In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.