Mathematics
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Circles
9 Likes
Answer
We know that,
The tangent at any point of a circle and the radius through this point are perpendicular to each other.
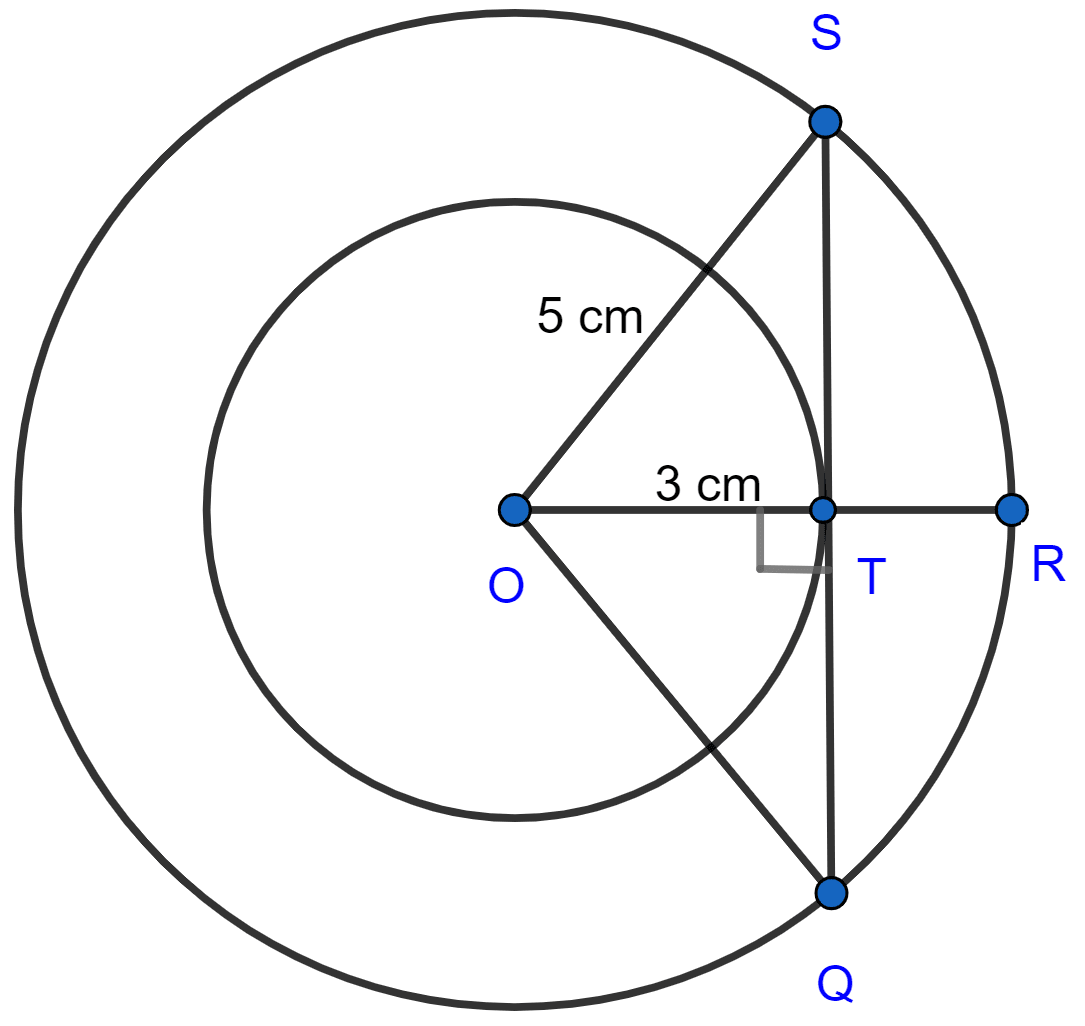
In right triangle OST, we have
⇒ OS2 = OT2 + ST2
⇒ 52 = 32 + ST2
⇒ ST2 = 25 - 9
⇒ ST2 = 16
⇒ ST =
⇒ ST = 4 cm.
Similarly, in right triangle OQT, we have
⇒ OQ2 = OT2 + QT2
⇒ 52 = 32 + QT2
⇒ QT2 = 25 - 9
⇒ QT2 = 16
⇒ QT =
⇒ QT = 4 cm.
From figure,
QS = ST + QT = 4 + 4 = 8 cm.
Hence, the length of a chord of the outer circle which touches the inner = 8 cm.
Answered By
6 Likes
Related Questions
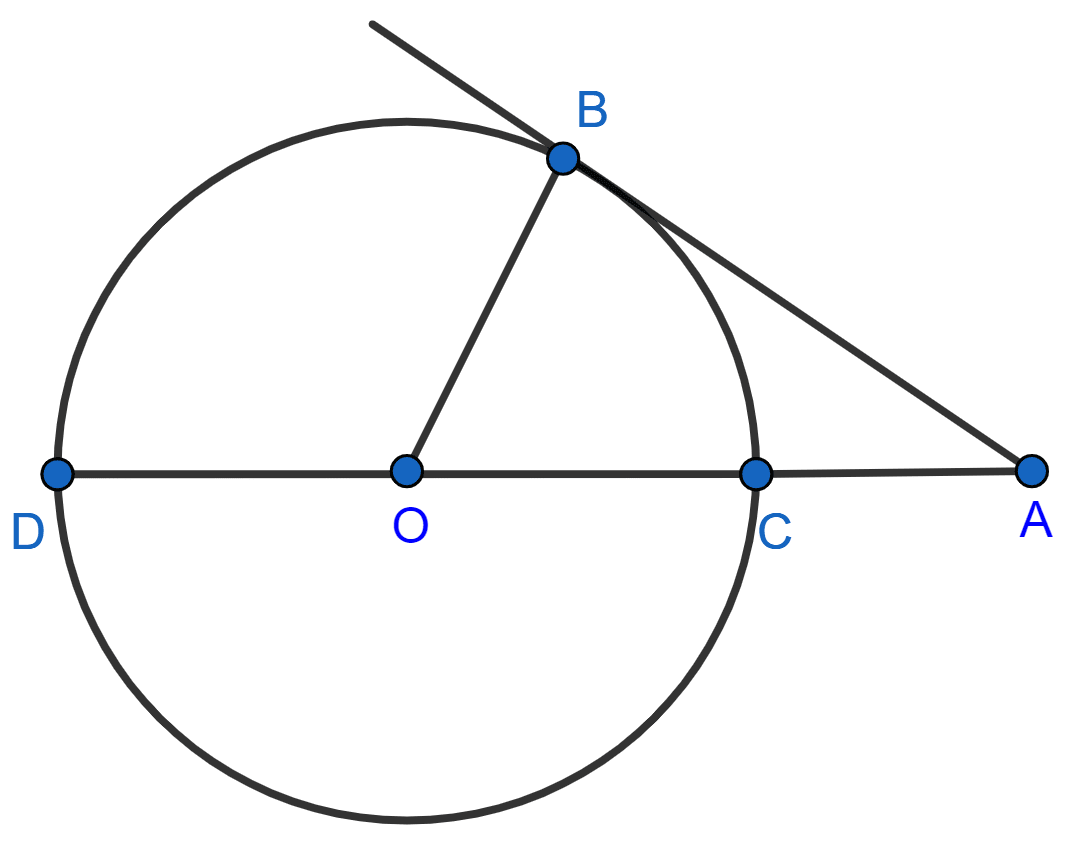
In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
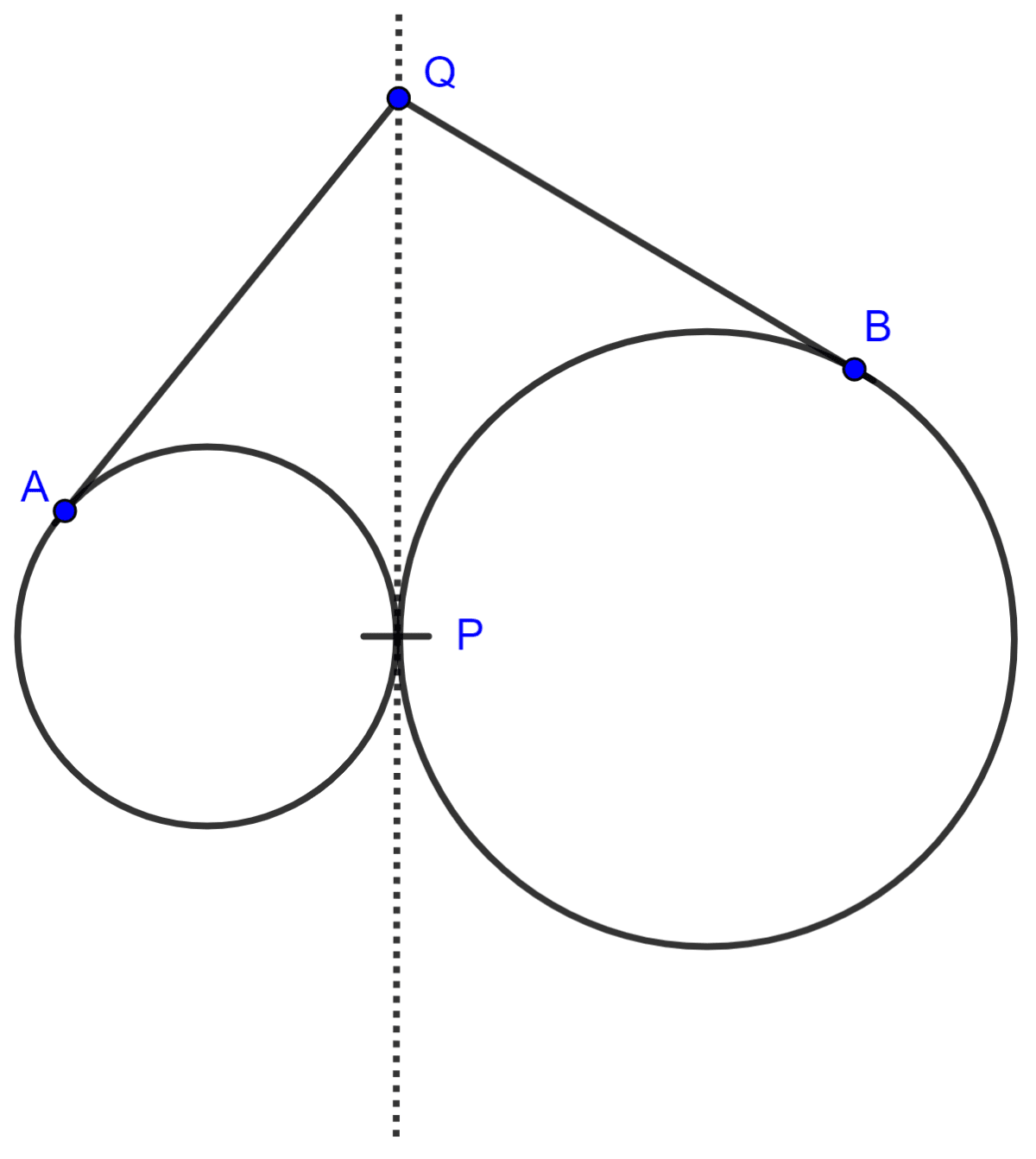
Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.