Mathematics
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4. Calculate the value of ratio: (i) PL/PQ and then LM/QR (ii) Area of △ LMN/Area of △ MNR (iii) Area of △ LQM/Area of △ LQN
Related Questions
In the given figure, AX : XB = 3 : 5.
Find :
(i) the length of BC, if the length of XY is 18 cm.
(ii) the ratio between the areas of trapezium XBCY and triangle ABC.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
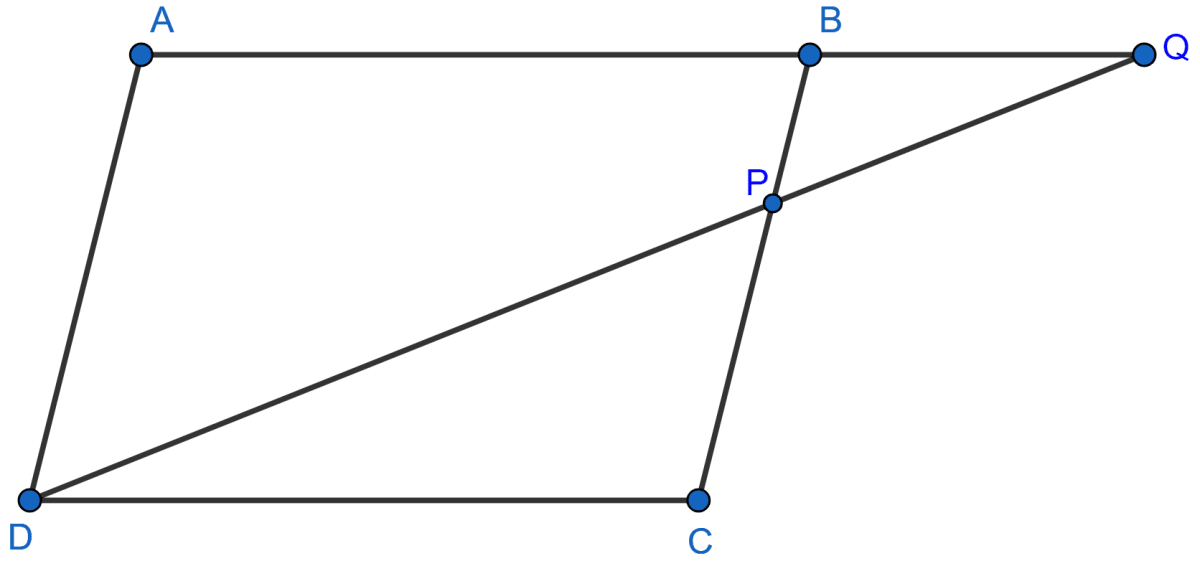
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm2.
Calculate :
(i) area of triangle CDP,
(ii) area of parallelogram ABCD.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC.
Also, find the area of triangle BCD.
