Mathematics
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Similarity
12 Likes
Answer
Triangle ABC is shown in the figure below:
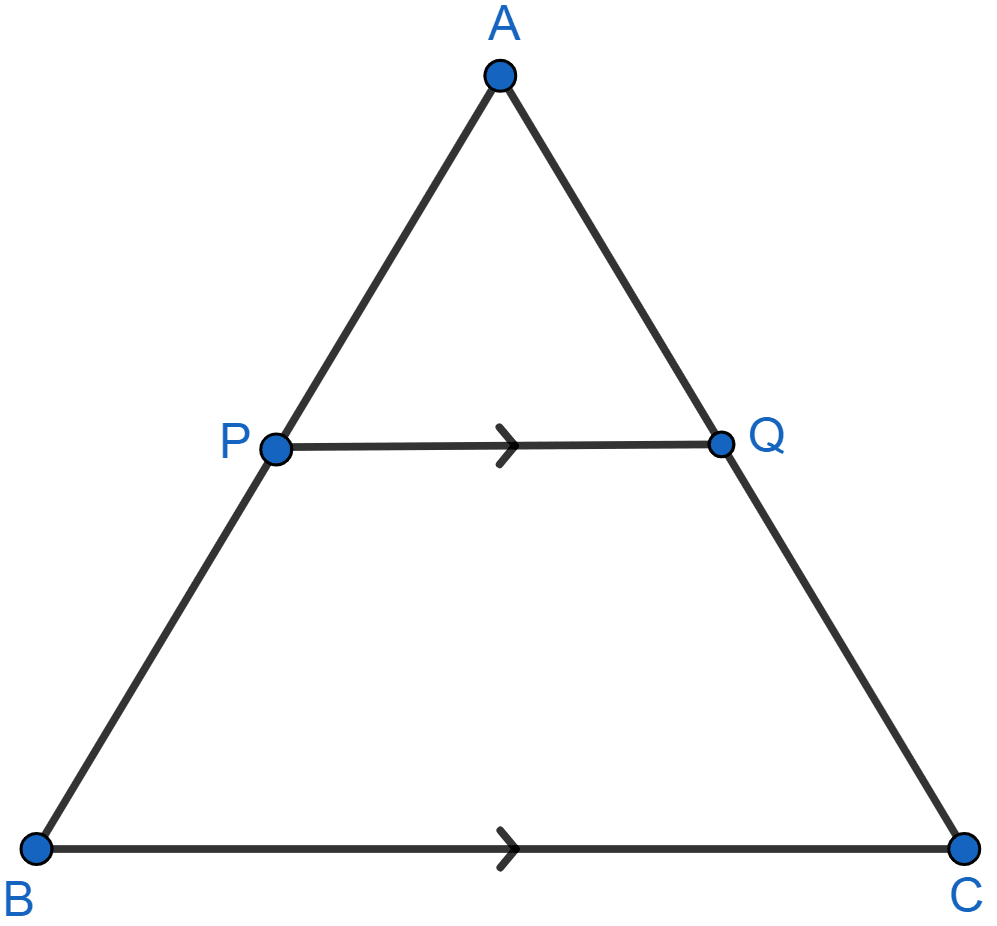
In ΔAPQ and ΔABC,
∠PAQ = ∠BAC [Common]
∠APQ = ∠ABC [Corresponding angles are equal]
∴ ΔAPQ ~ ΔABC [By AA].
According to question,
Area of ΔAPQ = Area of ΔABC
We know that,
The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Let AP = x and AB = x
From figure,
BP = AB - AP =
Hence, BP : AB = = .
Answered By
7 Likes
Related Questions
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
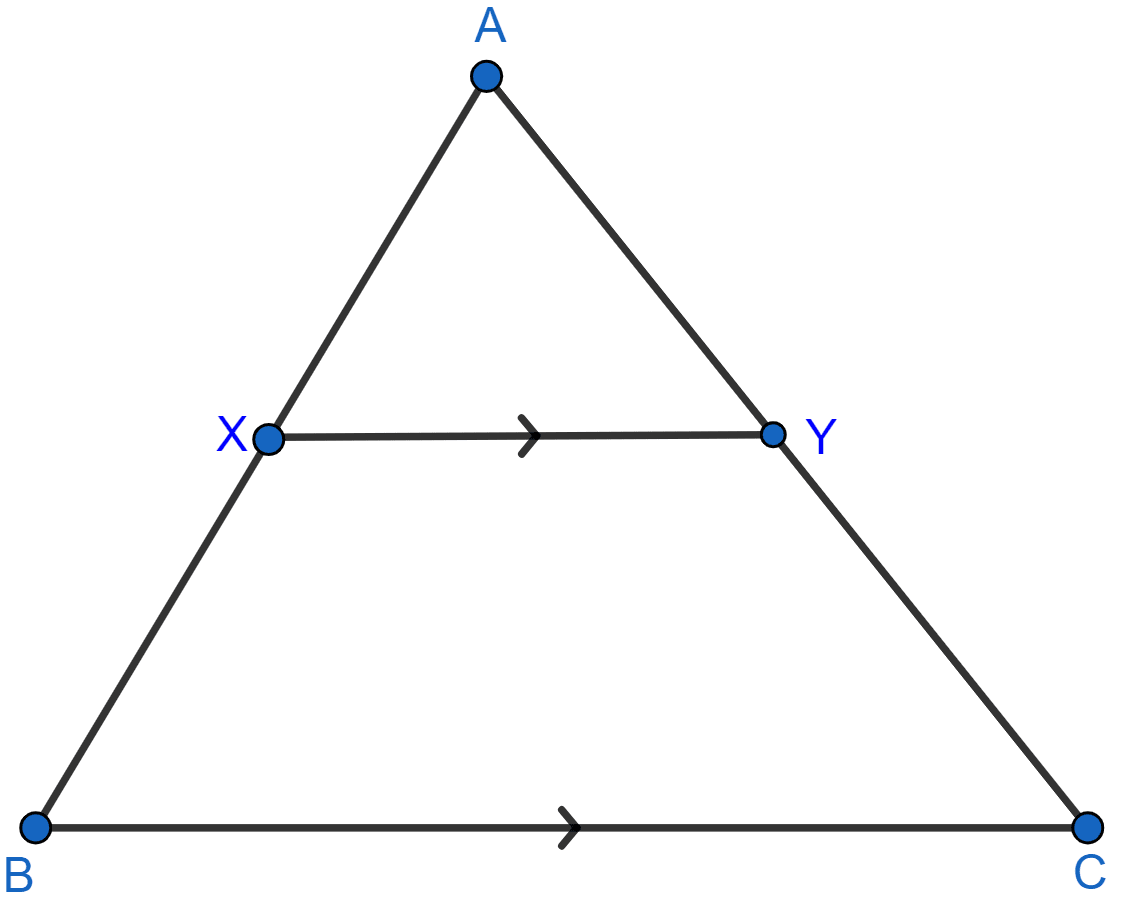
In the given figure, AX : XB = 3 : 5.
Find :
(i) the length of BC, if the length of XY is 18 cm.
(ii) the ratio between the areas of trapezium XBCY and triangle ABC.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
Calculate the value of ratio:
(i)
(ii)
(iii)
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm2.
Calculate :
(i) area of triangle CDP,
(ii) area of parallelogram ABCD.
