Mathematics
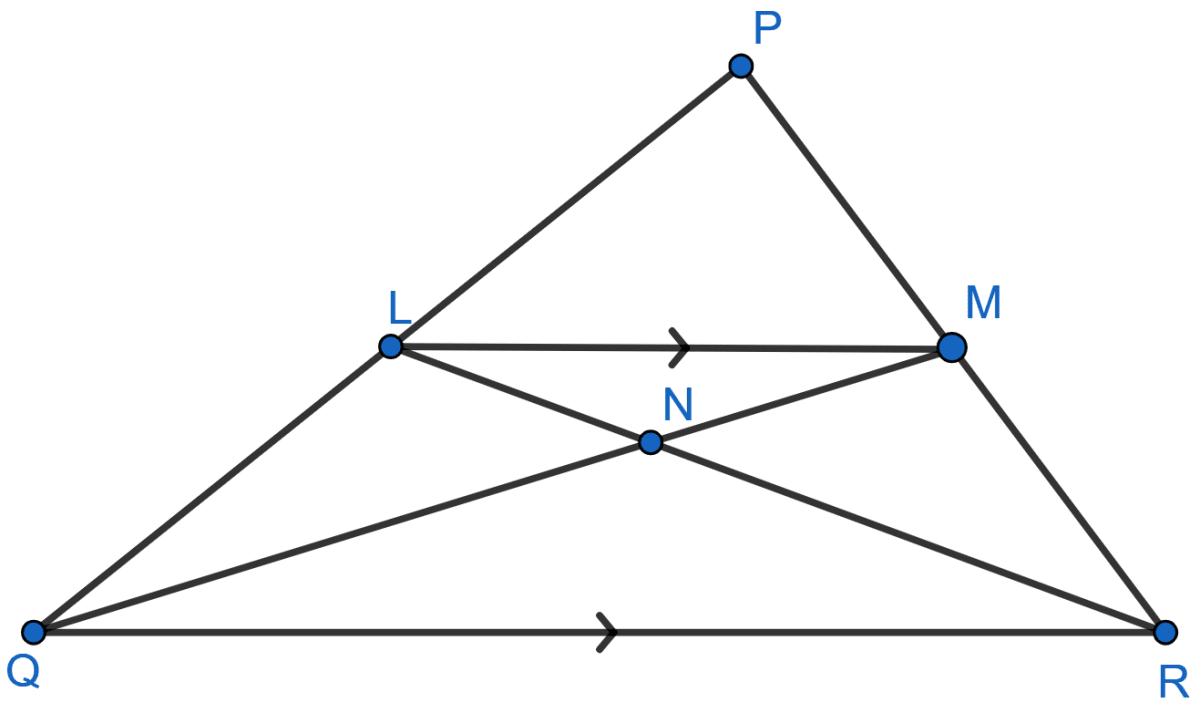
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.
Calculate the value of ratio:
(i)
(ii)
(iii)
Similarity
38 Likes
Answer
(i) Given,
Let PM = 3x and MR = 4x.
From figure,
PR = PM + MR = 3x + 4x = 7x.
.
In ΔPLM and ΔPQR,
As LM || QR, corresponding angles are equal.
∠PLM = ∠PQR
∠PML = ∠PRQ
∴ ∆PLM ~ ∆PQR [By AA]
Since, corresponding sides of similar triangles are proportional to each other we have :
Hence, PL : PQ = 3 : 7 and LM : QR = 3 : 7.
(ii) As ΔLMN and ΔMNR have common vertex at M and their bases LN and NR are along the same straight line.
…..(1)
Now, in ΔLMN and ΔRNQ we have,
⇒ ∠NLM = ∠NRQ [Alternate angles are equal]
⇒ ∠LMN = ∠NQR [Alternate angles are equal]
∴ ∆LNM ~ ∆RNQ [By AA]
Since corresponding sides of similar triangle are proportional to each other, we have :
Substituting value in (1) we get :
.
(iii) From part (ii) we get :
Let MN = 3a and QN = 7a
From figure,
MQ = MN + QN = 3a + 7a = 10a.
As ΔLQM and ΔLQN have common vertex at L and their bases QM and QN are along the same straight line.
.
Hence,
Answered By
23 Likes
Related Questions
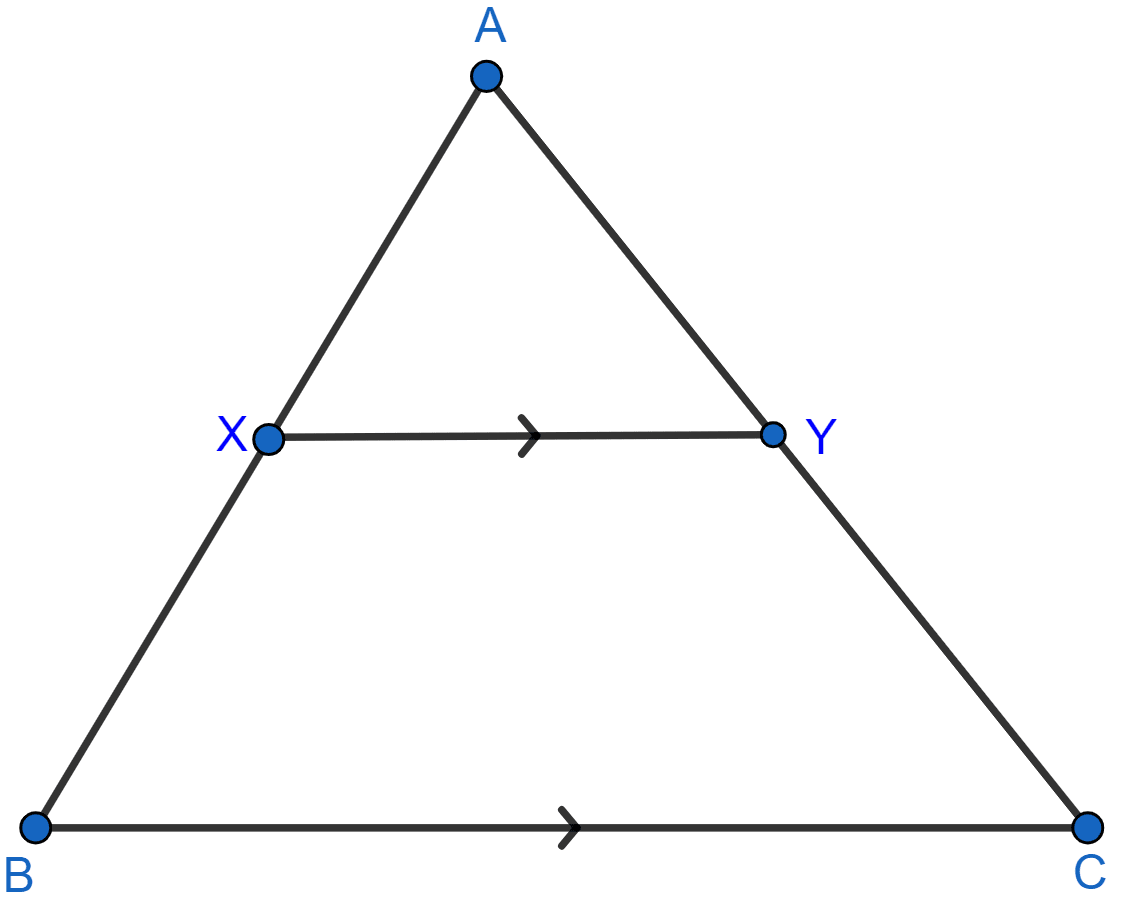
In the given figure, AX : XB = 3 : 5.
Find :
(i) the length of BC, if the length of XY is 18 cm.
(ii) the ratio between the areas of trapezium XBCY and triangle ABC.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm2.
Calculate :
(i) area of triangle CDP,
(ii) area of parallelogram ABCD.

In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC.
Also, find the area of triangle BCD.
