Mathematics
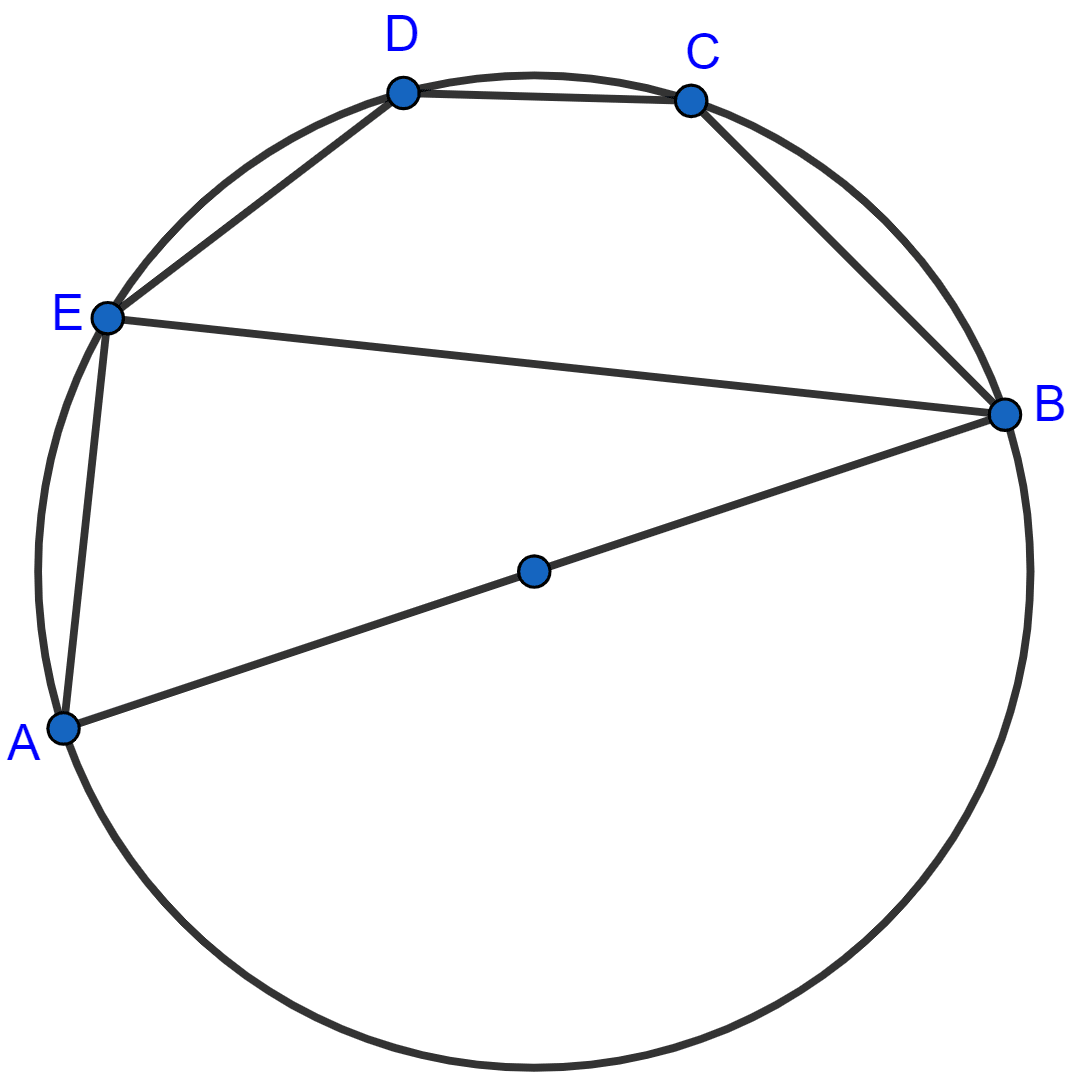
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate :
(i) ∠EBA,
(ii) ∠BCD.
Answer
(i) We know that,
Angle in semi-circle is a right angle.
∴ ∠AEB = 90°.
In △AEB,
⇒ ∠AEB + ∠EBA + ∠EAB = 180°
⇒ 90° + ∠EBA + 63° = 180°
⇒ 153° + ∠EBA = 180°
⇒ ∠EBA = 180° - 153° = 27°.
Hence, ∠EBA = 27°.
(ii) As, AB || ED
∴ ∠DEB = ∠EBA = 27° [Alternate angles]
BCDE is a cyclic quadrilateral.
∴ ∠DEB + ∠BCD = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]
⇒ 27° + ∠BCD = 180°
⇒ ∠BCD = 180° - 27° = 153°.
Hence, ∠BCD = 153°.
Related Questions
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.

In the given figure, AB is a diameter of the circle with center O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC.
Also, show that the △AOD is an equilateral triangle.

In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
