Mathematics
In the given figure, AB is a diameter of the circle with center O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC.
Also, show that the △AOD is an equilateral triangle.

Circles
21 Likes
Answer
(i) ABCD is a cyclic quadrilateral.
∴ ∠DCB + ∠DAB = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]
⇒ ∠DAB = 180° - ∠DCB
⇒ ∠DAB = 180° - 120° = 60°.
Hence, ∠DAB = 60°.
(ii) We know that,
Angle in a semi-circle is a right angle.
∠ADB = 90°.
In △DAB,
⇒ ∠ADB + ∠DAB + ∠DBA = 180°
⇒ 90° + 60° + ∠DBA = 180°
⇒ 150° + ∠DBA = 180°
⇒ ∠DBA = 180° - 150° = 30°.
Hence, ∠DBA = 30°.
(iii) OD = OB (Radius of circle)
∴ ∠ODB = ∠OBD [Angles opposite to equal sides are equal]
From figure,
∠OBD = ∠DBA = 30°.
∴ ∠ODB = 30°.
As, DO || BC
∴ ∠DBC = ∠ODB = 30° [Alternate angles are equal.]
Hence, ∠DBC = 30°.
(iv) From figure,
∠ABC = ∠ABD + ∠DBC = 30° + 30° = 60°.
In cyclic quadrilateral ABCD,
∴ ∠ADC + ∠ABC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]
⇒ ∠ADC = 180° - ∠ABC
⇒ ∠ADC = 180° - 60° = 120°.
Hence, ∠ADC = 120°.
In △AOD,
OA = OD [Radius of same circle]
∠AOD = ∠DAO [Angles opposite to equal sides are equal]
From figure,
⇒ ∠DAO = ∠DAB = 60°.
∴ ∠AOD = ∠DAO = ∠ADO = 60°
Hence, proved that △AOD is an equilateral triangle.
Answered By
11 Likes
Related Questions
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate :
(i) ∠EBA,
(ii) ∠BCD.
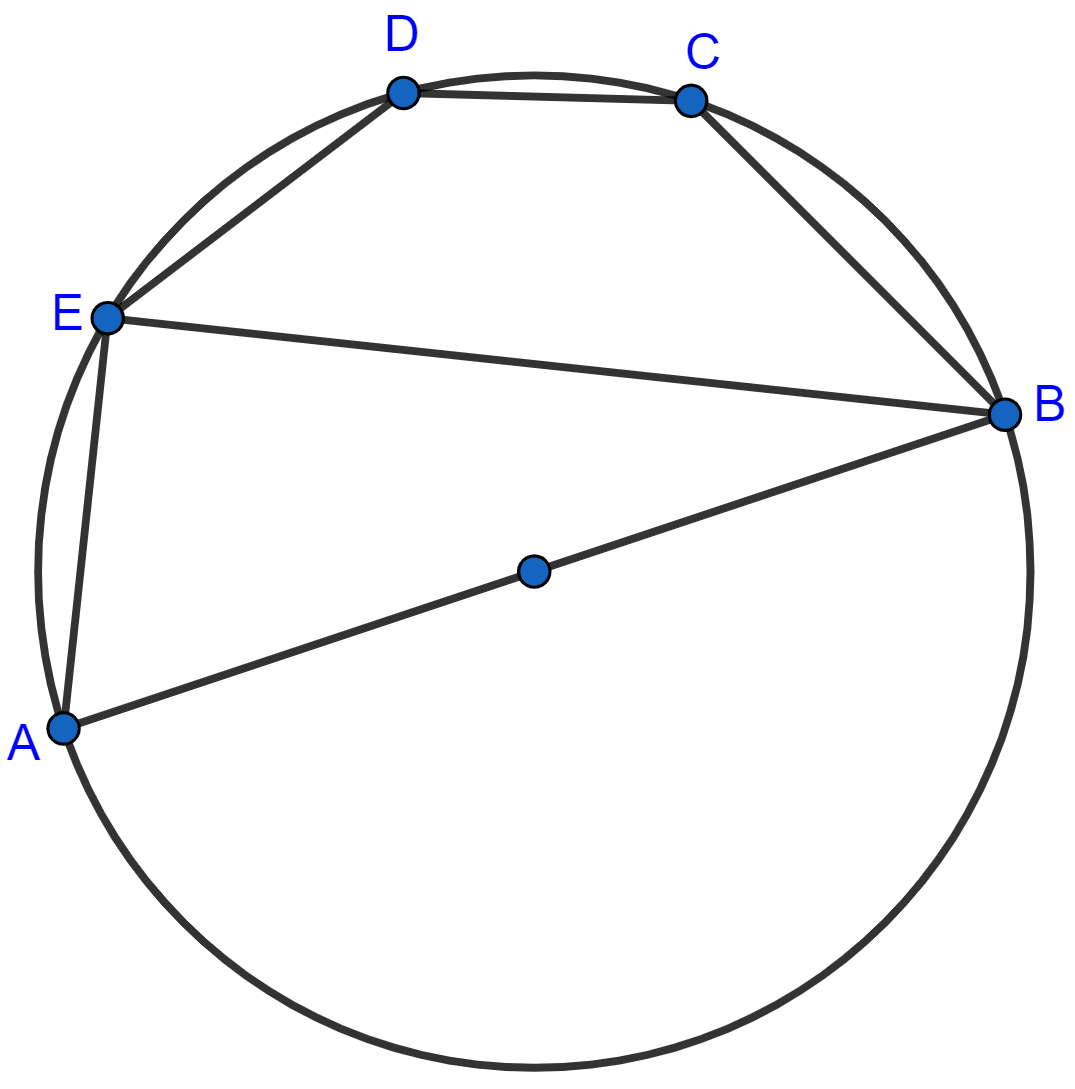
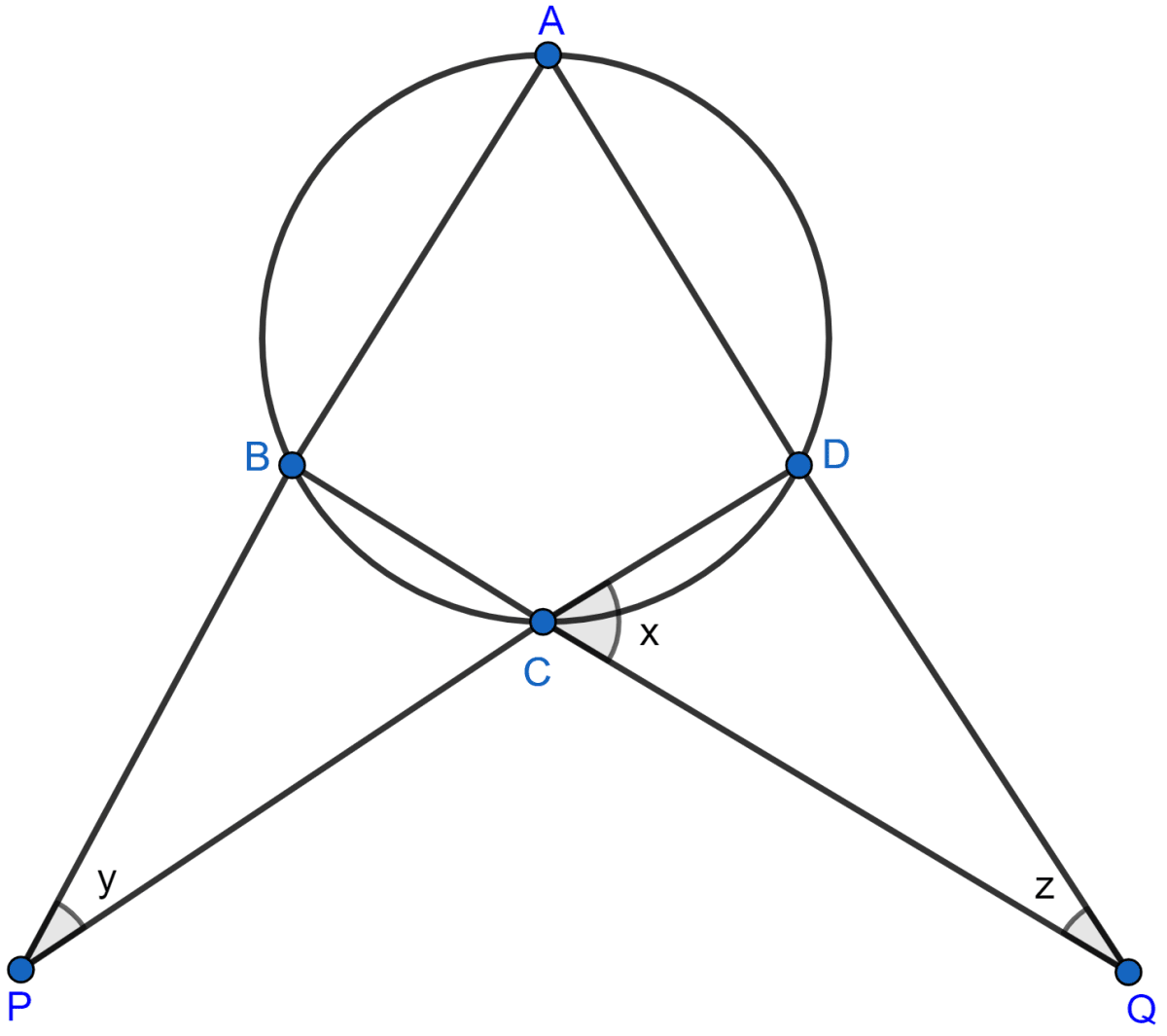
Calculate the angles x, y and z if :
In the given figure, AC is the diameter of the circle with center O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°. Calculate :
(i) Angle BEC,
(ii) Angle BCD,
(iii) Angle CED.
