Mathematics
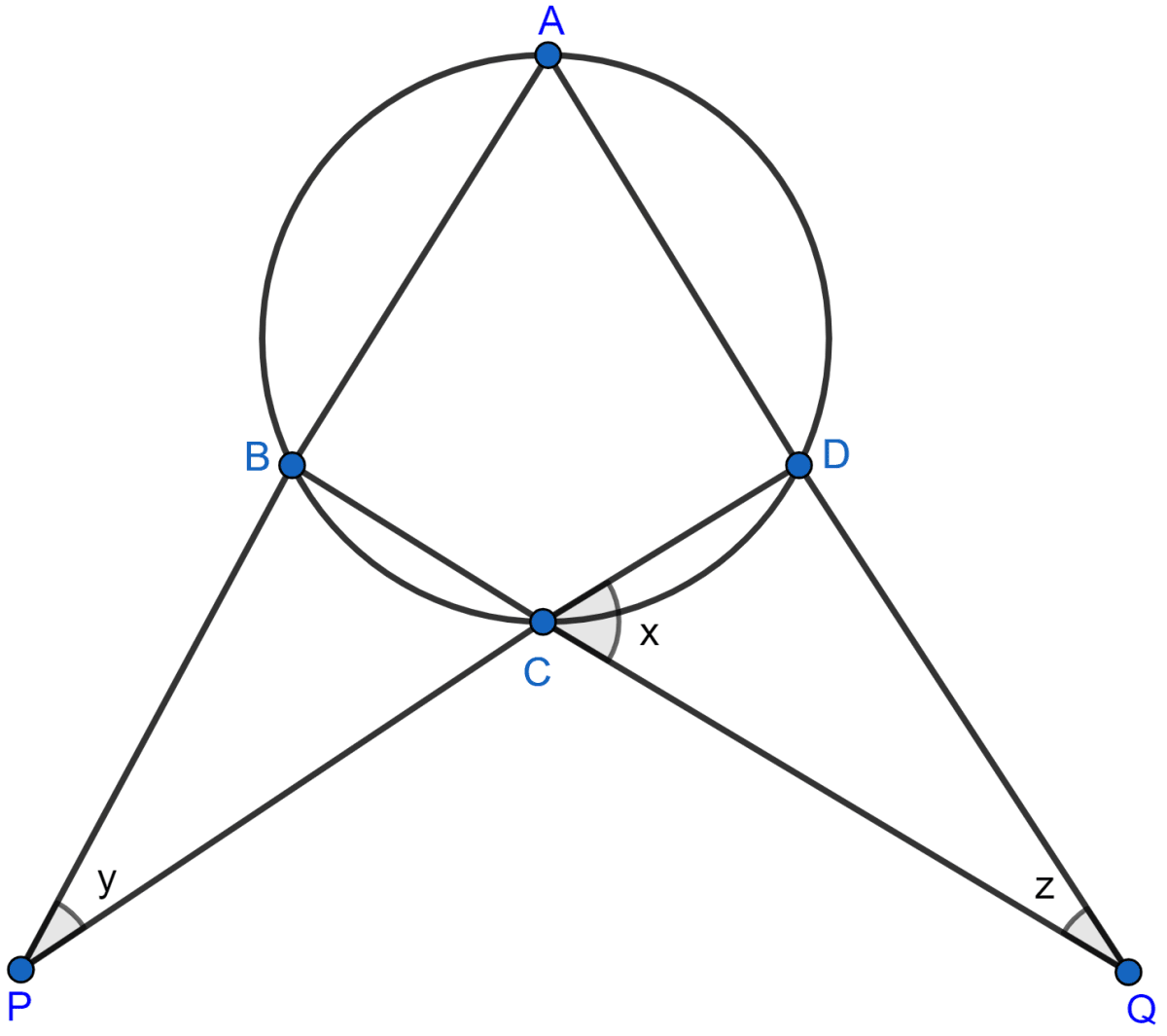
Calculate the angles x, y and z if :
Circles
19 Likes
Answer
Let = k.
∴ x = 3k, y = 4k and z = 5k.
From figure,
∠BCP = ∠DCQ [Vertically opposite angles are equal.]
Exterior angle of a triangle is equal to the sum of two opposite interior angles.
∠ABC = ∠BCP + ∠BPC = x + y = 3k + 4k = 7k
∠ADC = ∠DCQ + ∠DQC = x + z = 3k + 5k = 8k.
ABCD is a cyclic quadrilateral.
We know that,
⇒ ∠ABC + ∠ADC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]
⇒ 8k + 7k = 180°
⇒ 15k = 180°
⇒ k = = 12°.
x = 3k = 3 x 12° = 36°
y = 4k = 4 x 12° = 48°
z = 5k = 5 x 12° = 60°.
Hence, x = 36°, y = 48° and z = 60°.
Answered By
12 Likes
Related Questions
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate :
(i) ∠EBA,
(ii) ∠BCD.
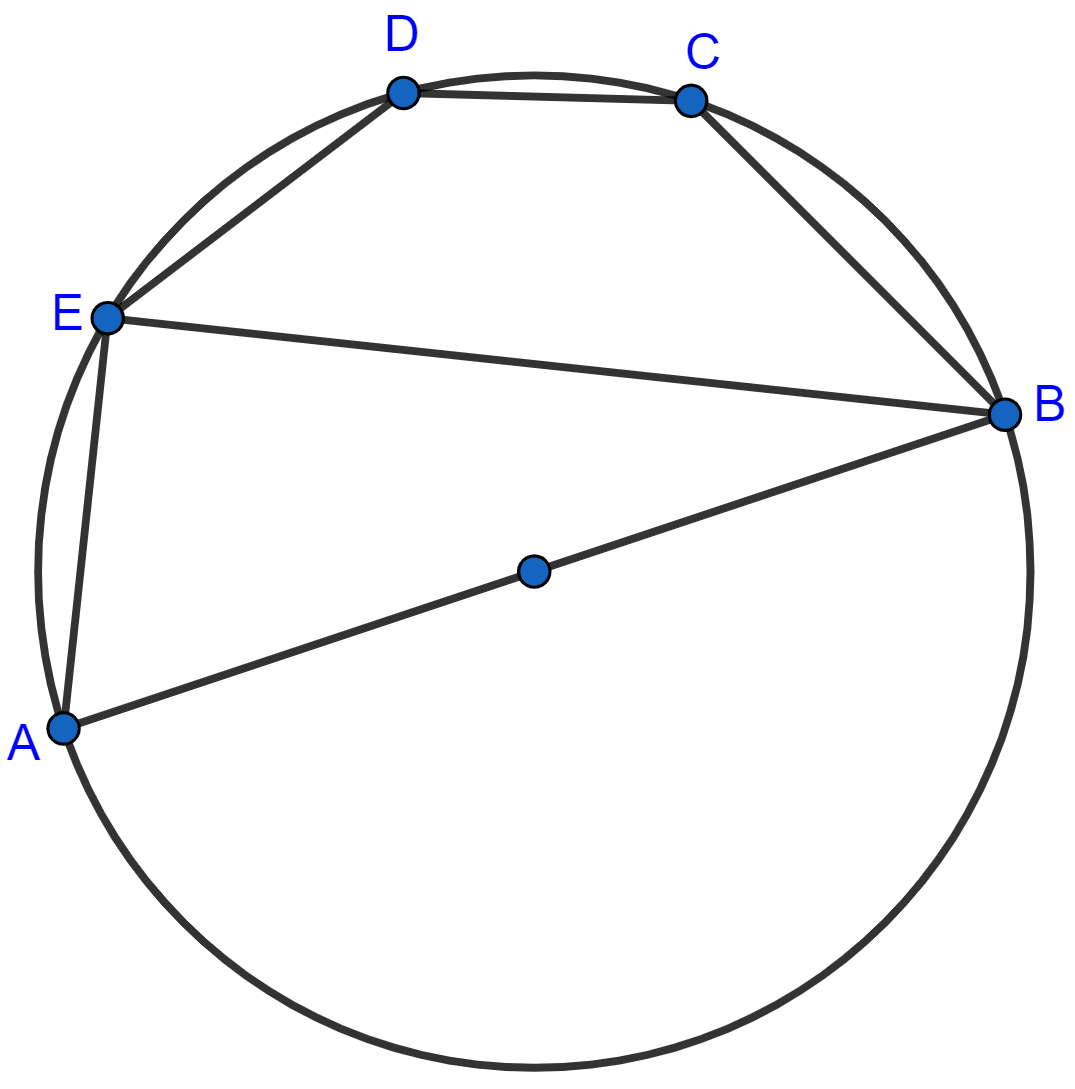
In the given figure, AB is a diameter of the circle with center O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC.
Also, show that the △AOD is an equilateral triangle.

In the given figure, AC is the diameter of the circle with center O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°. Calculate :
(i) Angle BEC,
(ii) Angle BCD,
(iii) Angle CED.

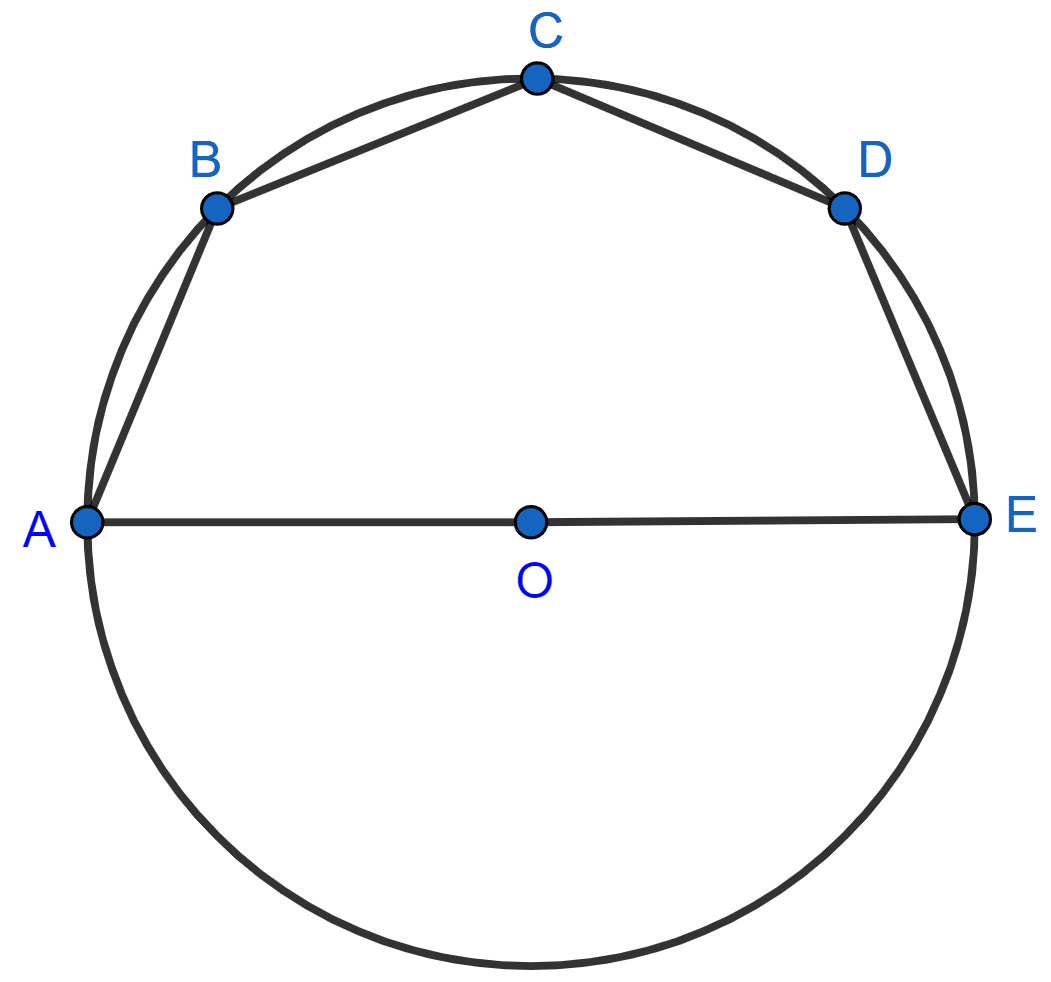
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.