Mathematics
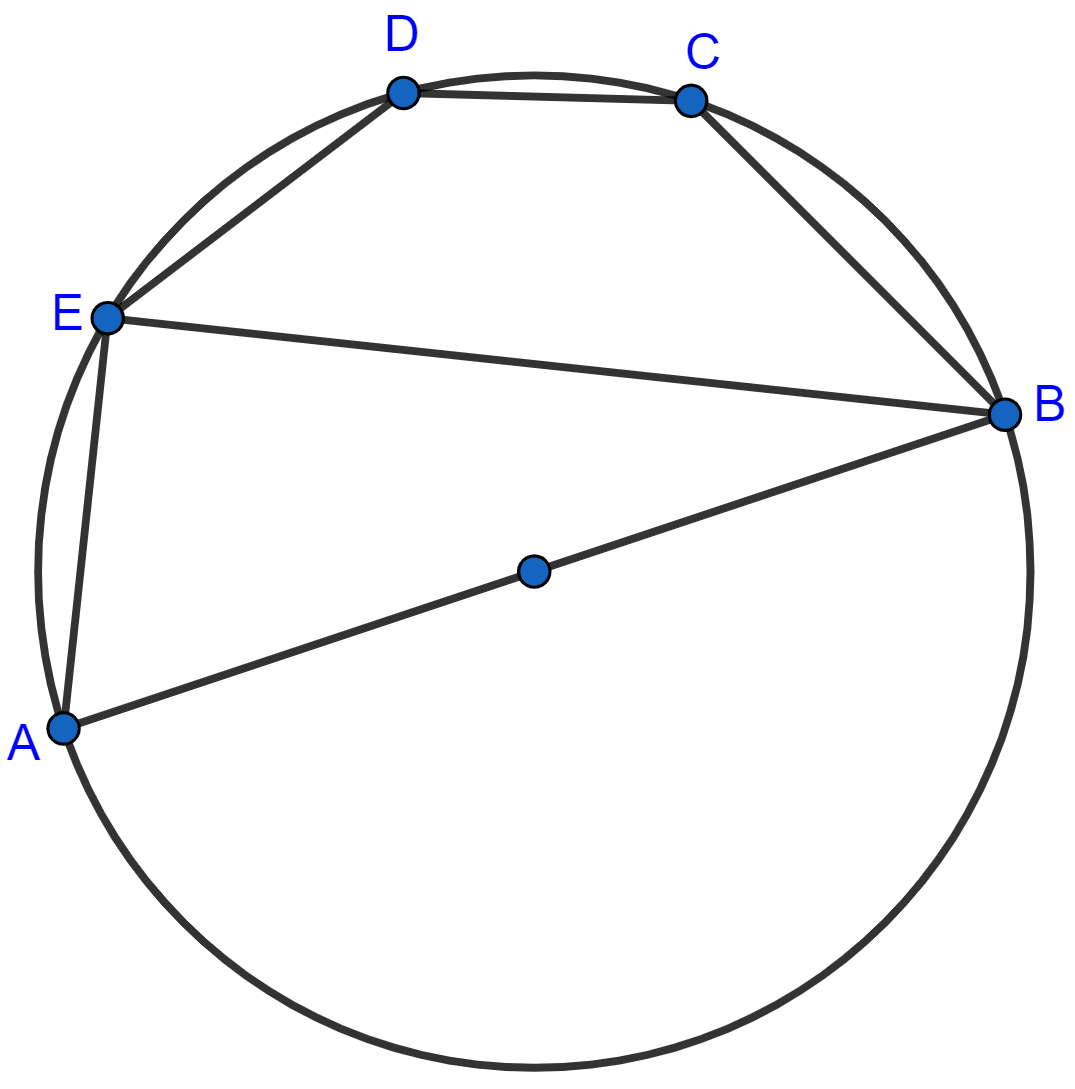
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.
Circles
10 Likes
Answer
(i) We know that,
Angles in same segment are equal.
∴ ∠DAB = ∠BED = 65°.
Hence, ∠DAB = 65°.
(ii) We know that,
Angle in semi-circle is a right angle.
∴ ∠ADB = 90°.
In △ADB,
⇒ ∠ABD + ∠ADB + ∠DAB = 180°
⇒ ∠ABD + 90° + 65° = 180°
⇒ 155° + ∠ABD = 180°
⇒ ∠ABD = 180° - 155° = 25°.
As, AB || DC
∠BDC = ∠ABD = 25°.
Hence, ∠BDC = 25°.
Answered By
9 Likes
Related Questions
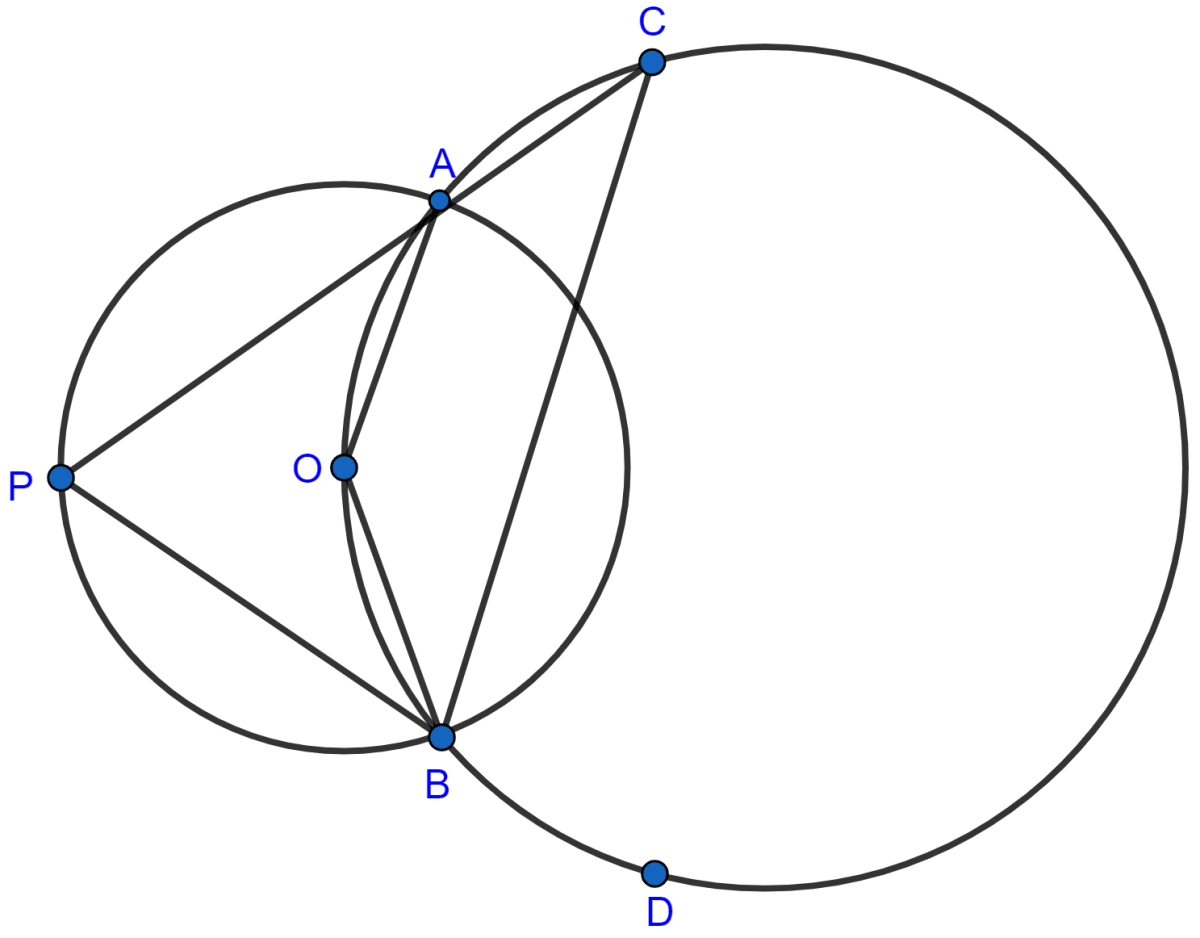
The figure shows two circles which intersect at A and B. The center of the smaller circle is O and lies on the circumference of the larger circle. Given ∠APB = a°.
Calculate, in terms of a°, the value of :
(i) obtuse ∠AOB,
(ii) ∠ACB,
(iii) ∠ADB.
Give reasons for your answers clearly.
In the given figure, AB is a diameter of the circle with center O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC.
Also, show that the △AOD is an equilateral triangle.
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate :
(i) ∠EBA,
(ii) ∠BCD.
