Mathematics
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that : ∠CAD = [∠PBA - ∠PAB]
Related Questions
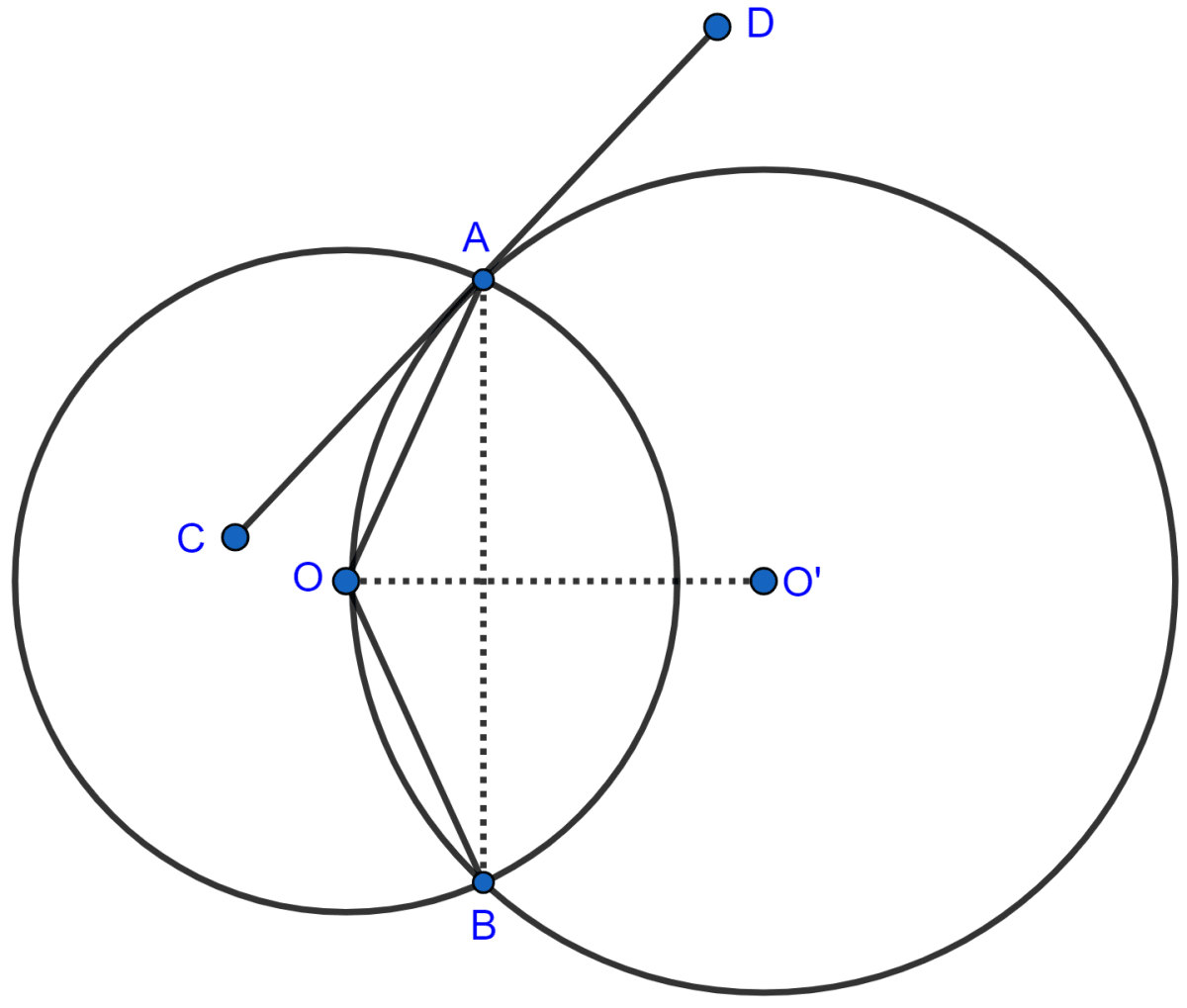
Two circles with centers O and O' are drawn to intersect each other at points A and B. Center O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with center O' at A. Prove that OA bisects angle BAC.
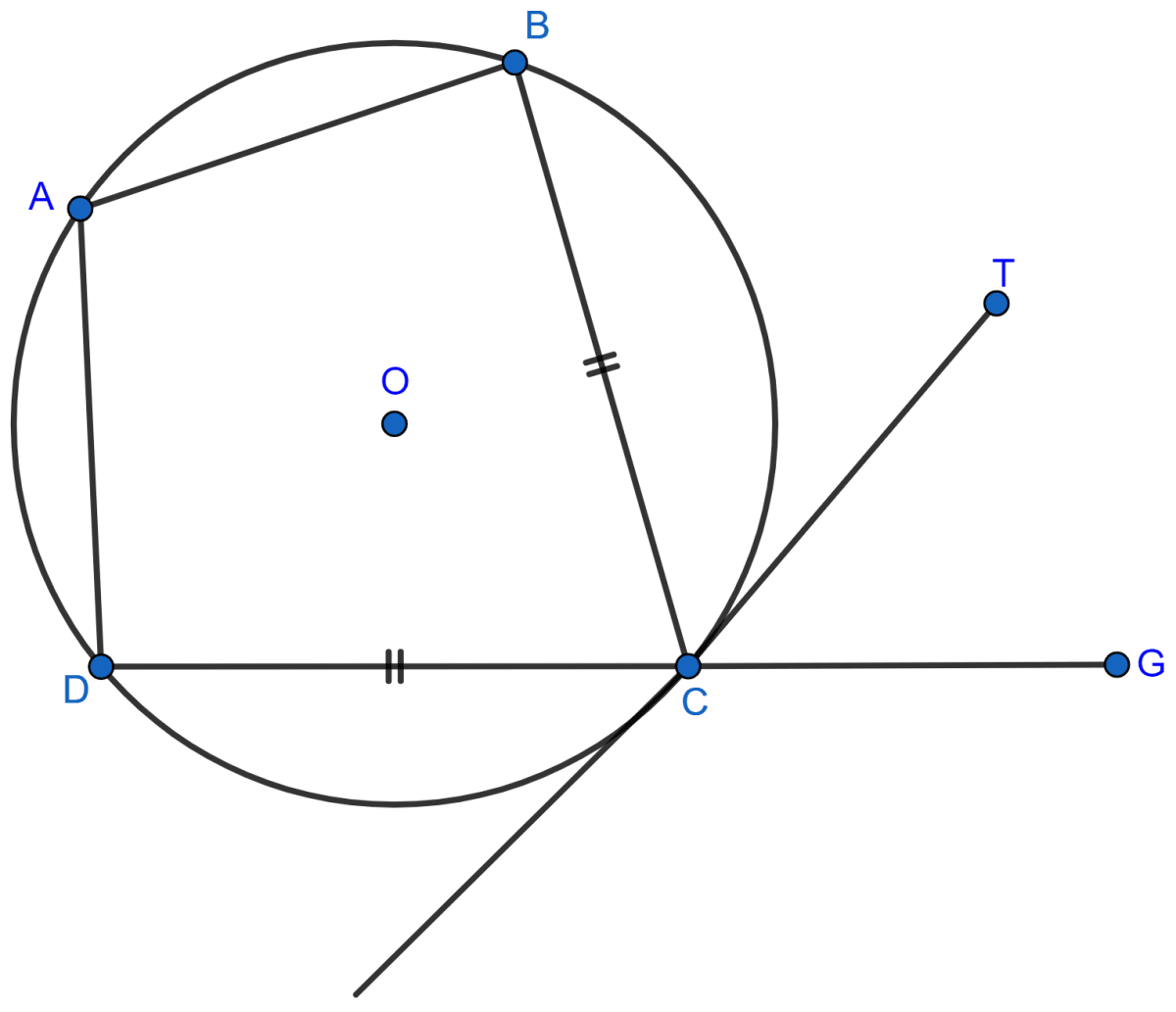
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the center of the circle, find :
(i) angle BCT
(ii) angle DOC
Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
![In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that ∠CAD = 1/2 [∠PBA - ∠PAB]. Tangents and Intersecting Chords, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q13-c18-ex-18-b-tangents-concise-maths-solutions-icse-class-10-1200x843.png)
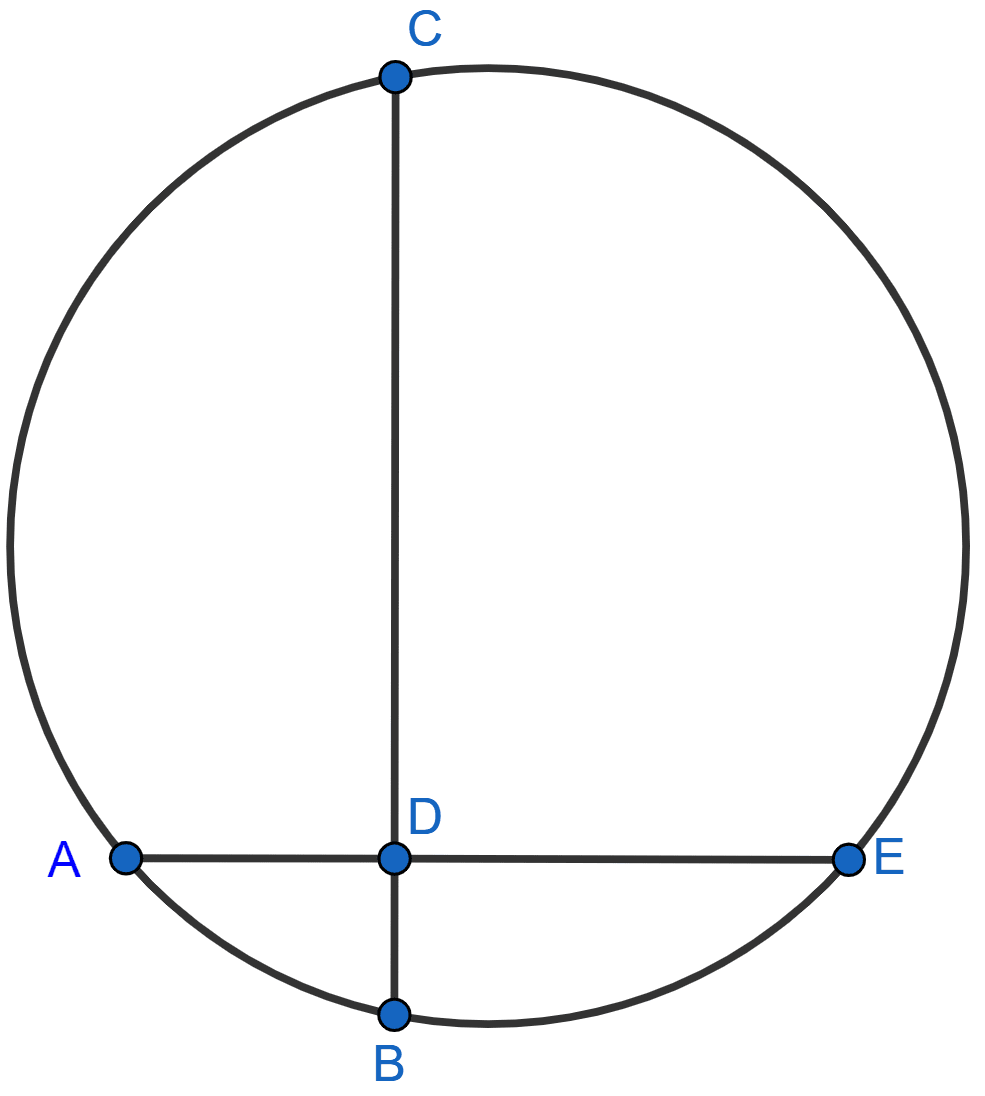
In the figure, chords AE and BC intersect each other at point D.
(i) If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.
(ii) If AD = BD, show that : AE = BC.