Mathematics
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that :
∠CAD = [∠PBA - ∠PAB]
![In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that ∠CAD = 1/2 [∠PBA - ∠PAB]. Tangents and Intersecting Chords, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q12-c18-ex-18-b-tangents-concise-maths-solutions-icse-class-10-1200x800.png)
Circles
30 Likes
Answer
As, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :
From figure,
PA is a tangent and AB is a chord.
∴ ∠PAB = ∠C [Angles in alternate segment are equal]………..(1)
Given,
AD is bisector of ∠BAC.
∴ ∠BAD = ∠DAC …….(2)
We know that,
An exterior angle is equal to sum of two opposite interior angles.
⇒ ∠ADP = ∠C + ∠DAC
⇒ ∠ADP = ∠PAB + ∠BAD [From (1) and (2)]
⇒ ∠ADP = ∠PAD
Since, sides opposite to equal sides are equal.
∴ PA = PD
∴ PAD is an isosceles triangle.
In △ABC,
⇒ ∠PBA = ∠C + ∠BAC [Exterior angle is equal to sum of two opposite interior angles]
⇒ ∠BAC = ∠PBA - ∠C
⇒ ∠BAC = ∠PBA - ∠PAB [As, ∠C = ∠PAB]
⇒ 2∠CAD = ∠PBA - ∠PAB [As, AD bisects ∠BAC]
⇒ ∠CAD = (∠PBA - ∠PAB).
Hence, proved that ∠CAD = (∠PBA - ∠PAB).
Answered By
19 Likes
Related Questions
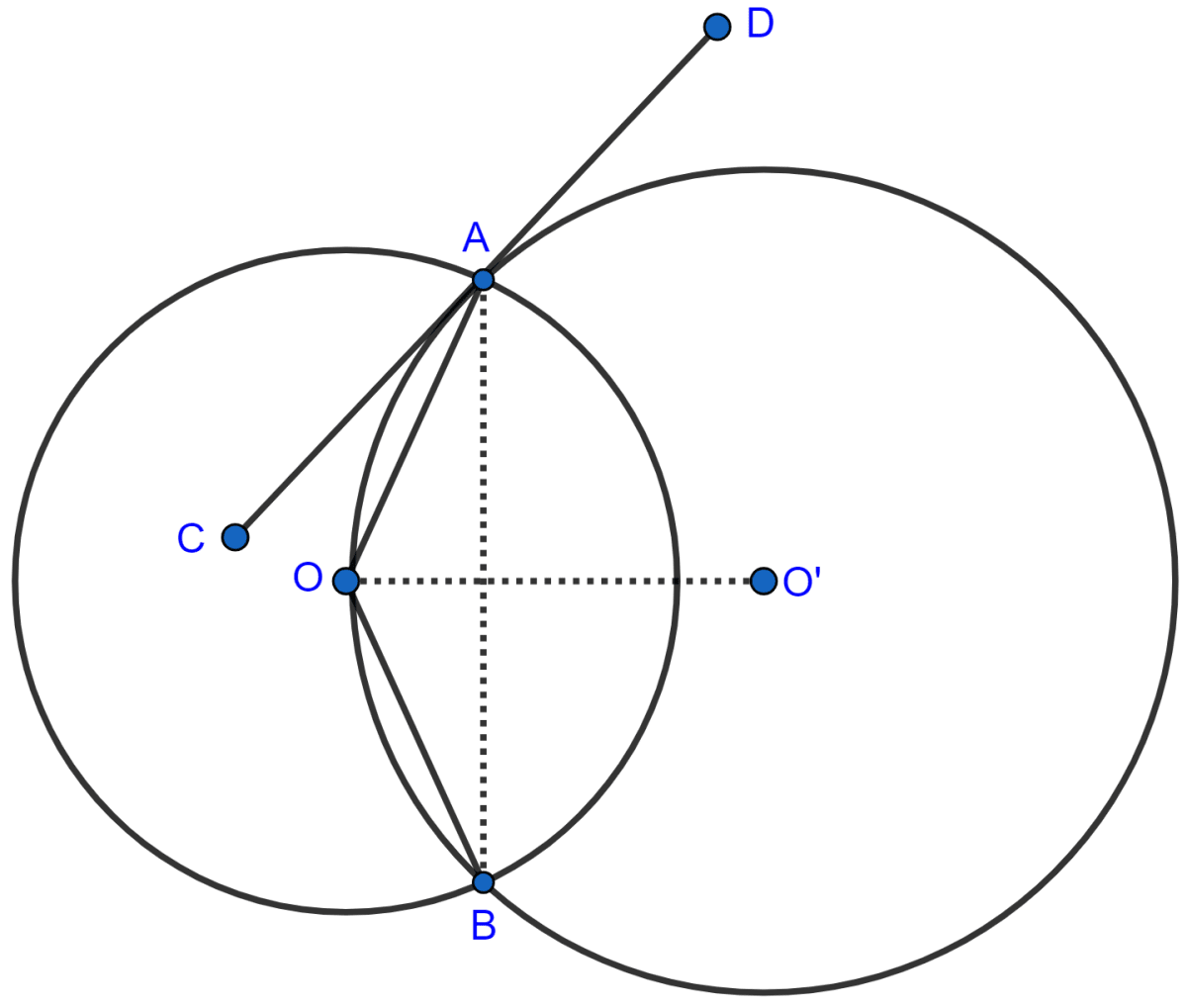
Two circles with centers O and O' are drawn to intersect each other at points A and B. Center O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with center O' at A. Prove that OA bisects angle BAC.
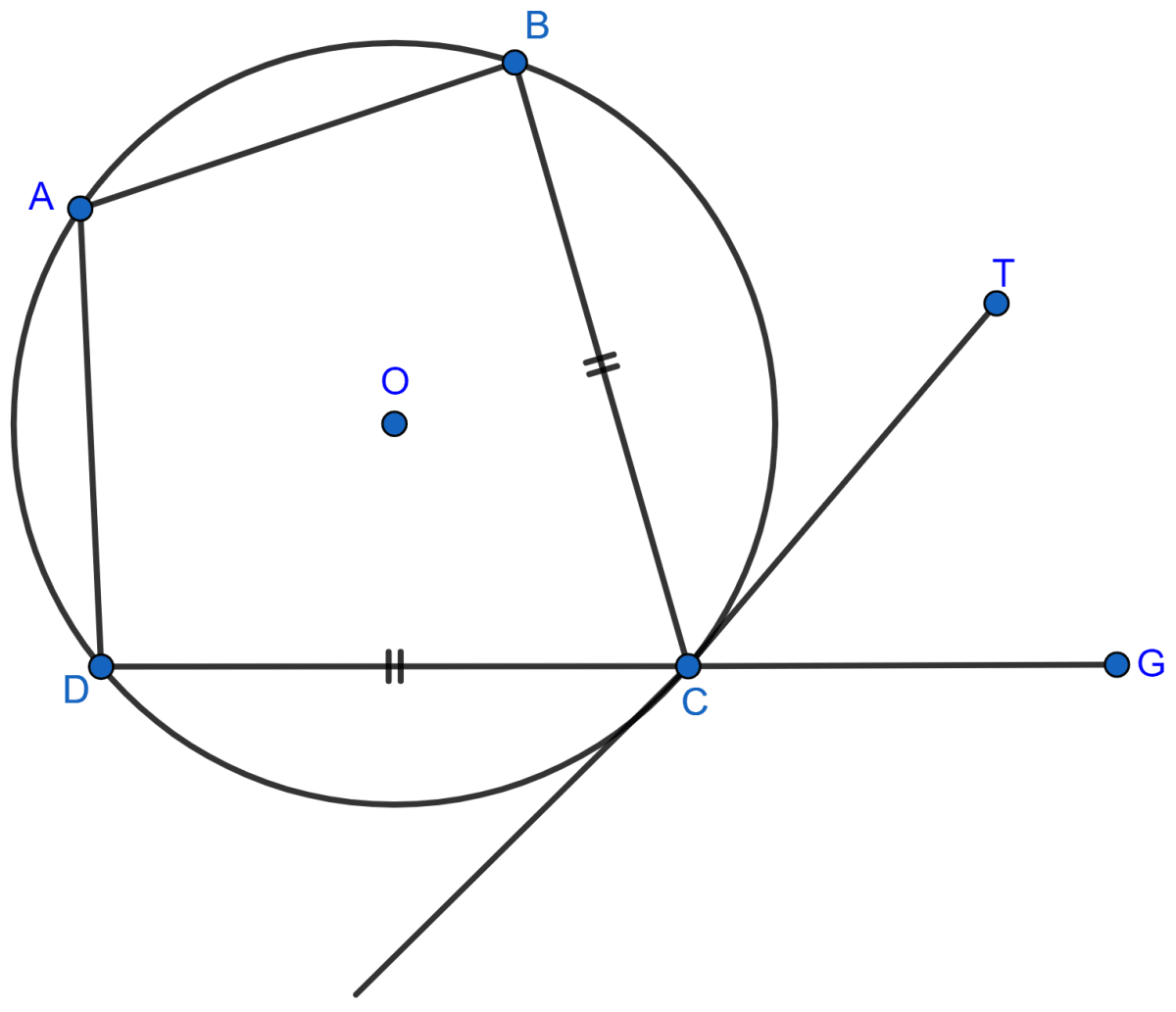
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the center of the circle, find :
(i) angle BCT
(ii) angle DOC
Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
![In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that ∠CAD = 1/2 [∠PBA - ∠PAB]. Tangents and Intersecting Chords, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q13-c18-ex-18-b-tangents-concise-maths-solutions-icse-class-10-1200x843.png)
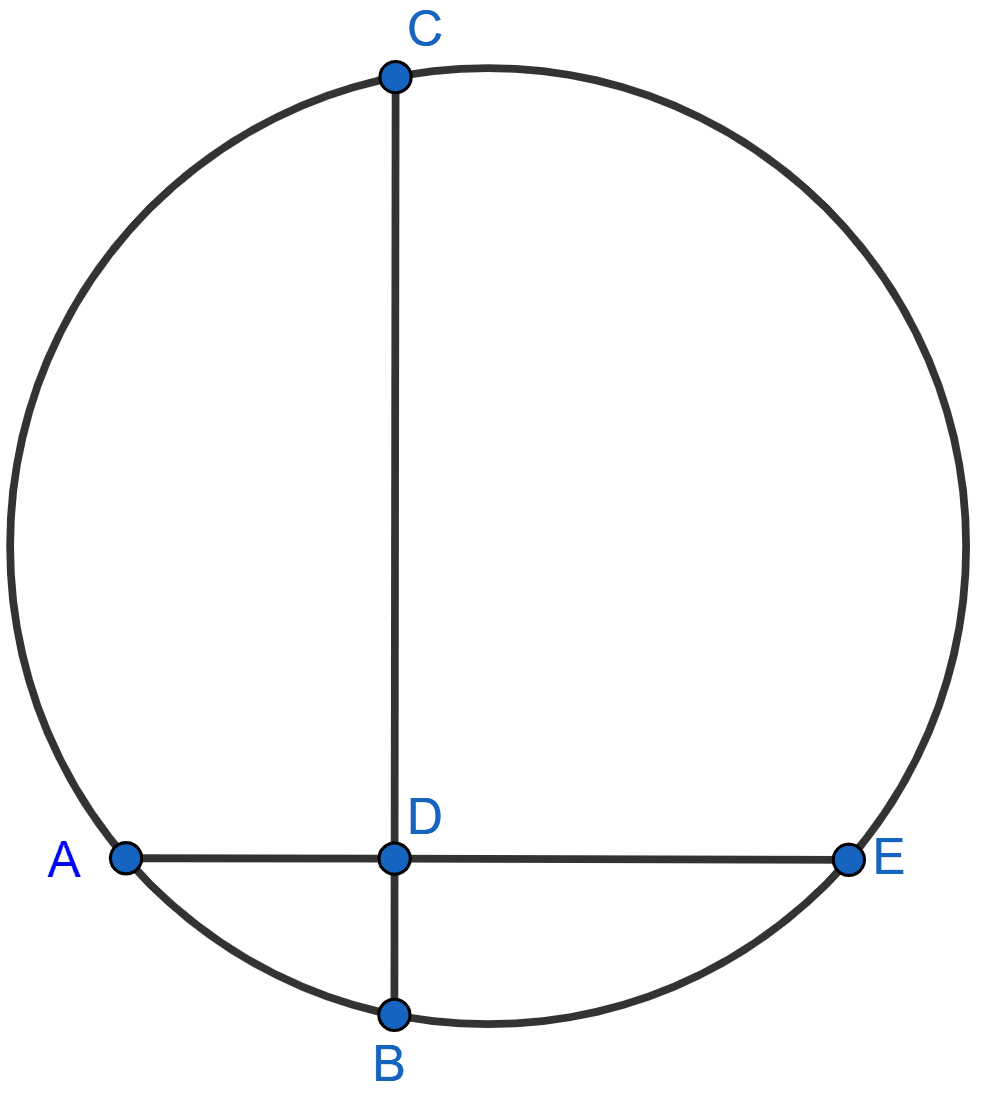
In the figure, chords AE and BC intersect each other at point D.
(i) If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.
(ii) If AD = BD, show that : AE = BC.