Mathematics
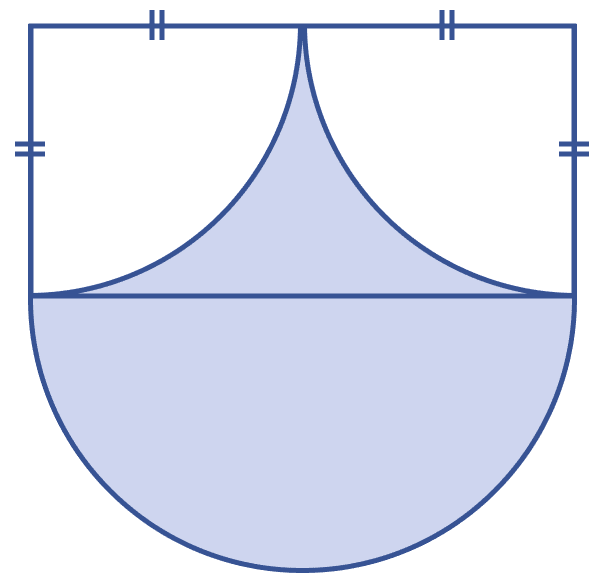
In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .
Mensuration
25 Likes
Answer
From figure,
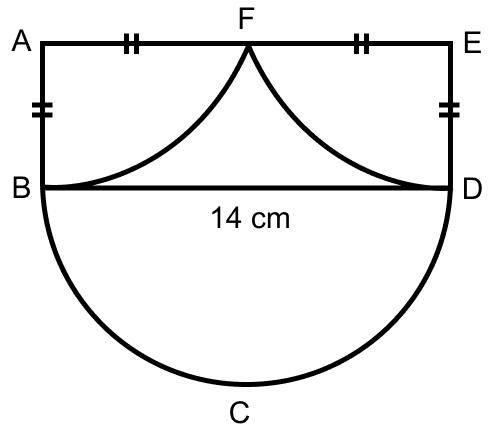
BD = 14 cm (Diameter of semi-circle)
AF = FE = x (let)
⇒ BD = AF + FE
⇒ 14 = x + x
⇒ 2x = 14
⇒ x = 7 cm.
Area of semi-circle BCD =
Area of quadrant ABF = Area of quadrant EDF =
From figure, AB = ED = AF = FE = 7 cm.
Area of rectangle ABDE= AB × BD = 7 × 14 = 98 cm2.
Area of shaded region = Area of rectangle ABDE + Area of semi-circle BCD - Area of quadrant ABF - Area of quadrant EDF
= 98 + 77 - 38.5 - 38.5
= 98 cm2.
Hence, area of shaded region = 98 cm2.
Answered By
16 Likes
Related Questions
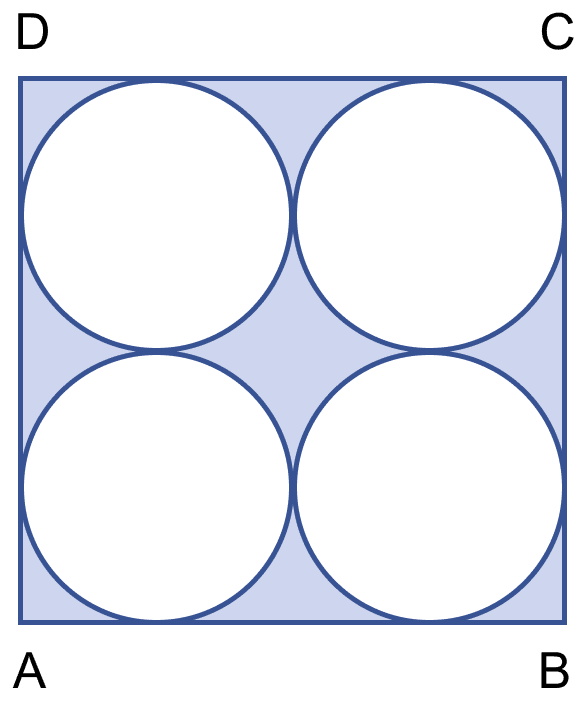
In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.

In the figure (ii) given below, area of △ABC = 35 cm2. Find the area of the shaded region.

Find the area and the perimeter of the shaded region in figure (i) given below. The dimensions are in centimeters.
