Mathematics
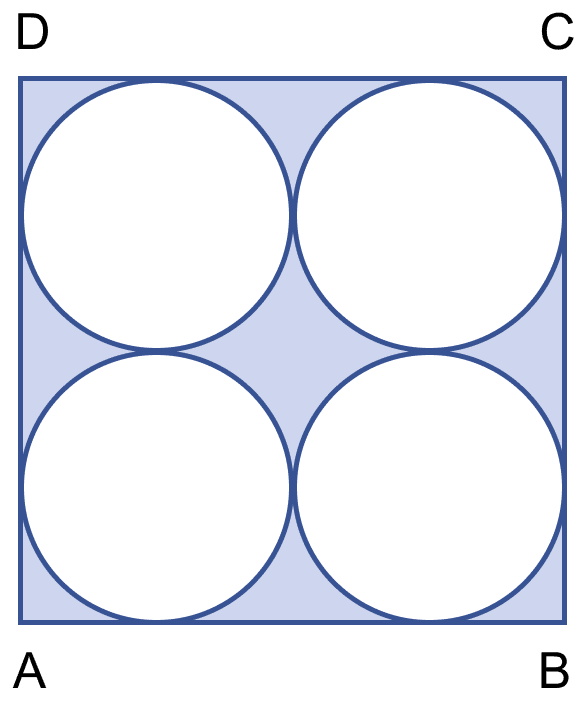
In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
Mensuration
26 Likes
Answer
Let radius of each circle be r cm.
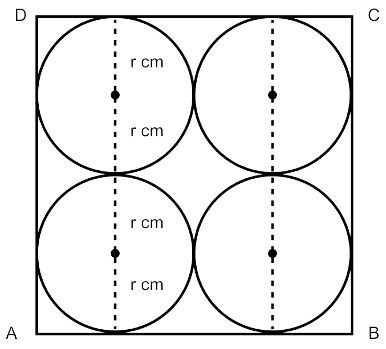
From figure,
⇒ r + r + r + r = 14
⇒ 4r = 14
⇒ r = 3.5 cm.
Since, radius is same so, each circle will have same area.
Area of each circle = πr2
=
=
= 22 × 0.5 × 3.5
= 38.5 cm2
Area of square = (side)2 = 142 = 196 cm2.
Area of shaded region = Area of square - Area of circles
= 196 - 4 × 38.5
= 196 - 154
= 42 cm2.
Hence, area of shaded region = 42 cm2.
Answered By
18 Likes
Related Questions
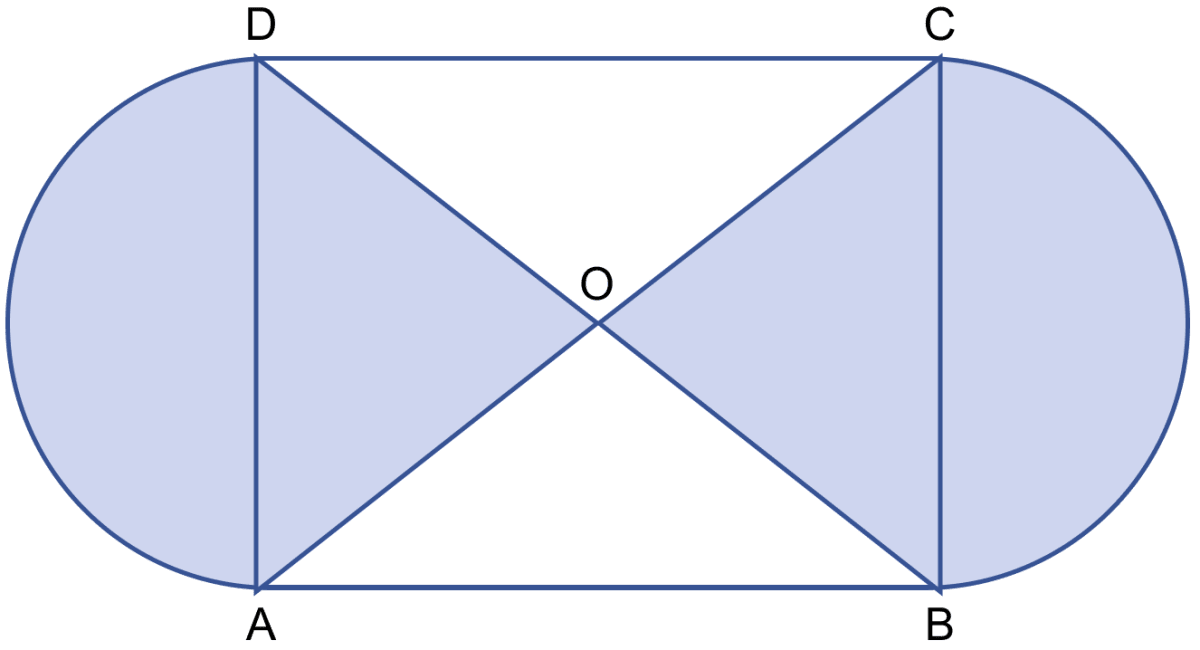
In the adjoining figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircle are drawn with AD and BC as diameters. Find the area of the shaded region. Take π = .
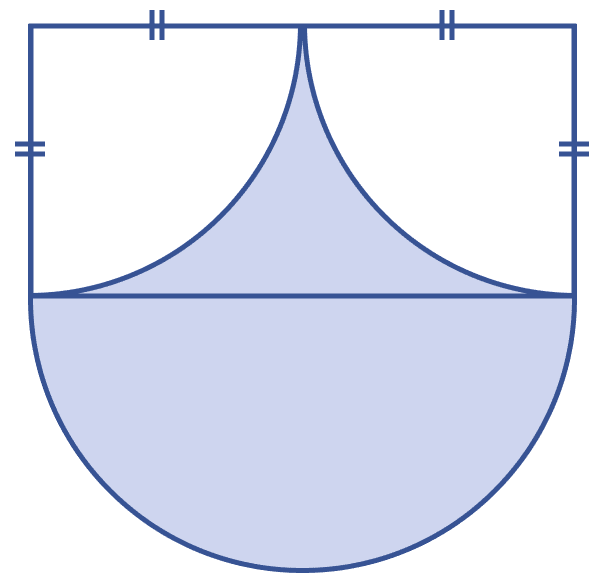
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.

In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .
Find the area and the perimeter of the shaded region in figure (i) given below. The dimensions are in centimeters.
