Mathematics
In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .
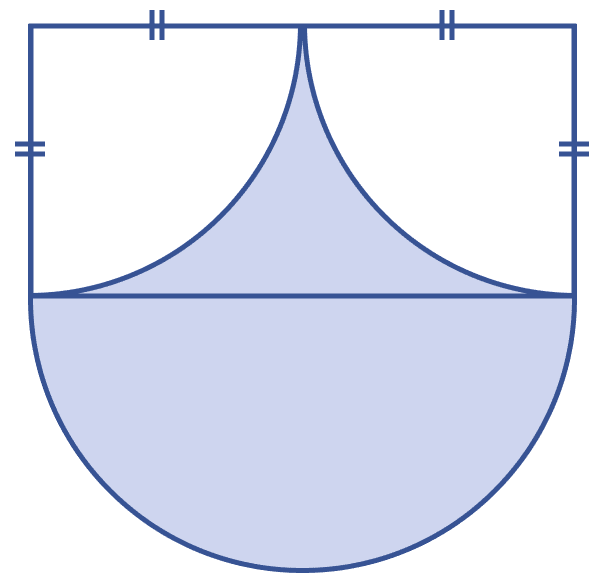
Mensuration
33 Likes
Answer
From figure,
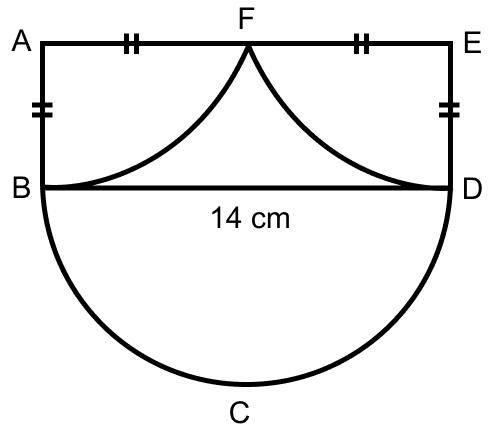
BD = 14 cm (Diameter of semi-circle)
AF = FE = x (let)
⇒ BD = AF + FE
⇒ 14 = x + x
⇒ 2x = 14
⇒ x = 7 cm.
Area of semi-circle BCD =
Area of quadrant ABF = Area of quadrant EDF =
From figure, AB = ED = AF = FE = 7 cm.
Area of rectangle ABDE= AB × BD = 7 × 14 = 98 cm2.
Area of shaded region = Area of rectangle ABDE + Area of semi-circle BCD - Area of quadrant ABF - Area of quadrant EDF
= 98 + 77 - 38.5 - 38.5
= 98 cm2.
Hence, area of shaded region = 98 cm2.
Answered By
21 Likes
Related Questions
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.

In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
Find the area and the perimeter of the shaded region in figure (i) given below. The dimensions are in centimeters.

In the figure (ii) given below, area of △ABC = 35 cm2. Find the area of the shaded region.
