Mathematics
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.

Mensuration
28 Likes
Answer
Area of square = (side)2 = 142 = 196 cm2.
From figure,
Diameter of both semicircle = side of square = 14 cm.
∴ Radius (r) = = 7 cm.
Area of both the semi-circles =
Area of shaded region = Area of square - Area of semi-circles
= 196 - 154 = 42 cm2.
From figure,
Perimeter = arc DPA + DC + arc CPB + AB
= πr + 14 + πr + 14
= 2πr + 28
= + 28
= 44 + 28 = 72 cm.
Hence, area of shaded region = 42 cm2 and perimeter = 72 cm.
Answered By
20 Likes
Related Questions
In the given figure, find the area of the unshaded portion within the rectangle.
(Take π = 3.14)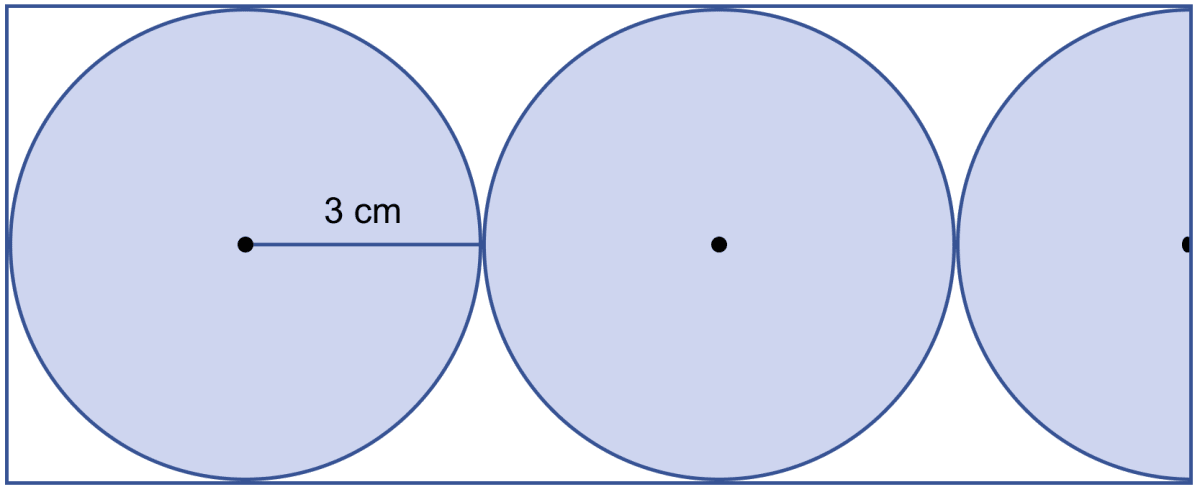
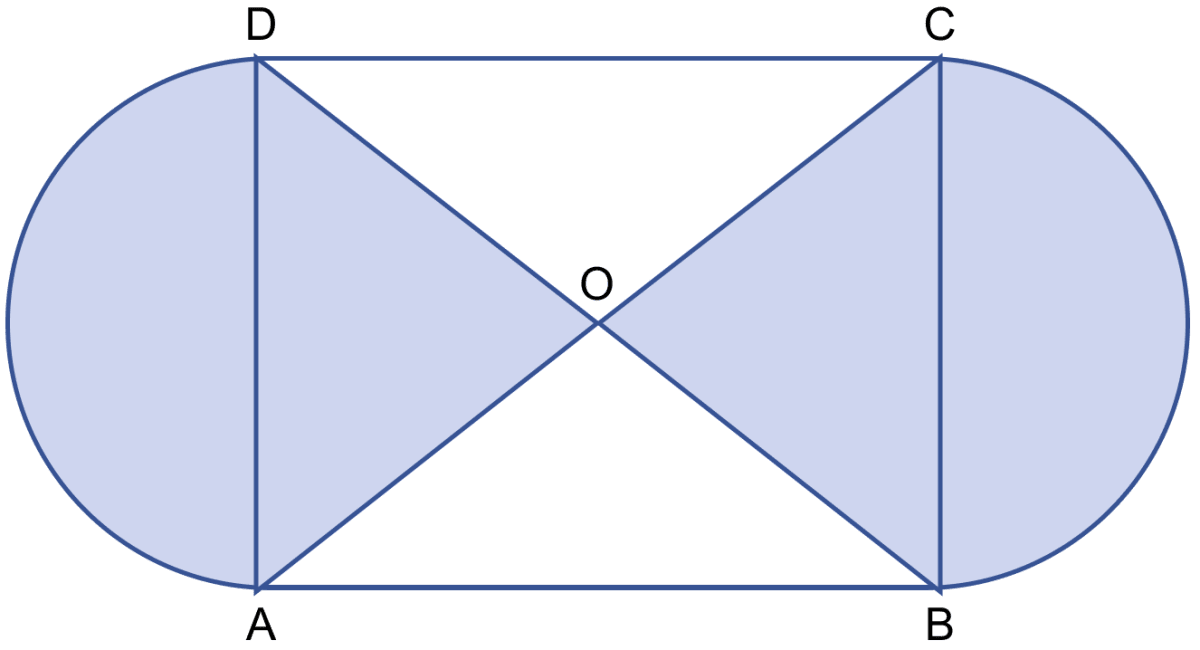
In the adjoining figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircle are drawn with AD and BC as diameters. Find the area of the shaded region. Take π = .
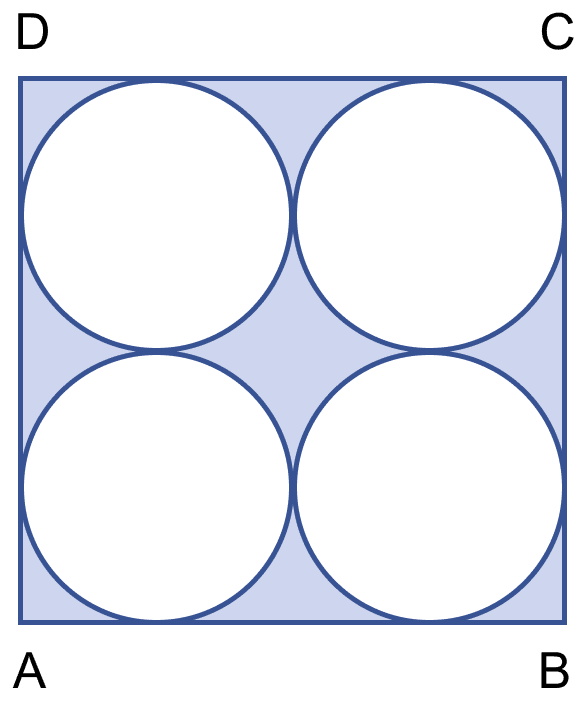
In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
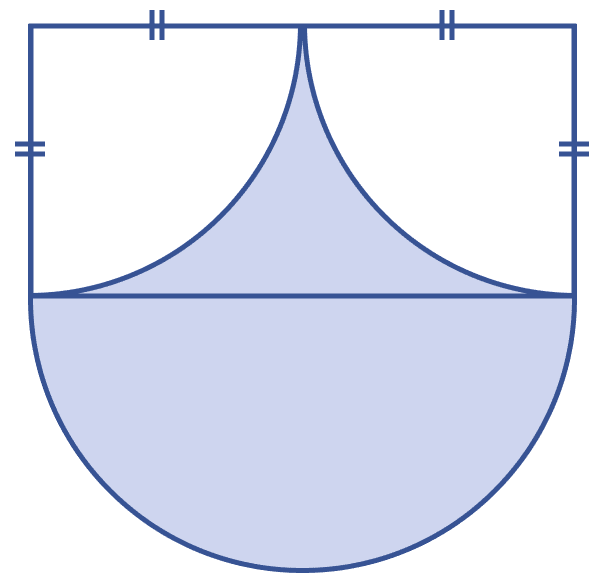
In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .