Mathematics
In the given figure, find the area of the unshaded portion within the rectangle.
(Take π = 3.14)
Mensuration
27 Likes
Answer
Let ABCD be a rectangle.
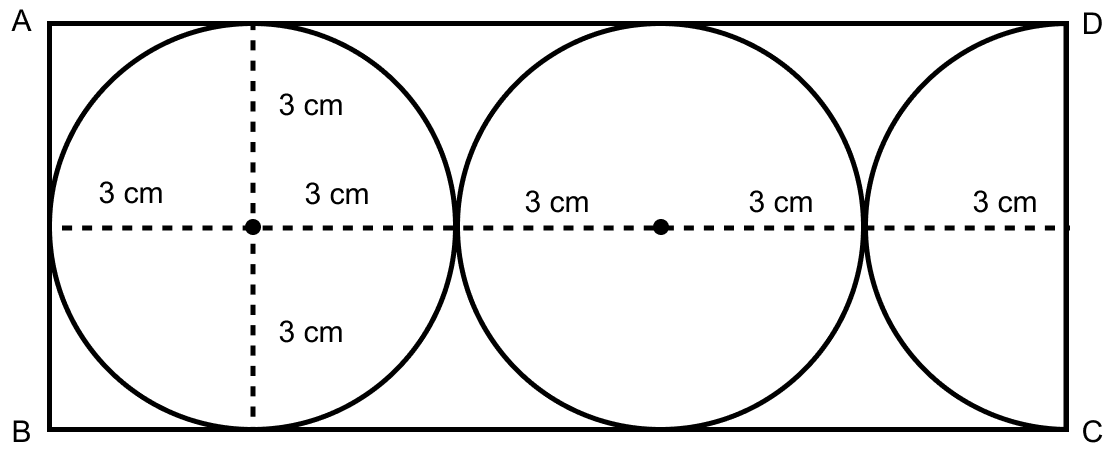
From figure,
AB = CD = 6 cm and,
AD = BC = 15 cm.
Area of rectangle = l × b = AD × AB = 15 × 6 = 90 cm2.
Area of shaded portion = π(3)2 + π(3)2 +
Area of unshaded region = Area of rectangle - Area of shaded region
= 90 - 70.65 = 19.35 cm2.
Hence, area of unshaded region = 19.35 cm2.
Answered By
16 Likes
Related Questions
A copper wire when bent in the form of an equilateral triangle has area cm2. If the same wire is bent in the form of a circle, find the area enclosed by the wire.
Find the circumference of the circle whose area is 16 times the area of the circle with diameter 7 cm.
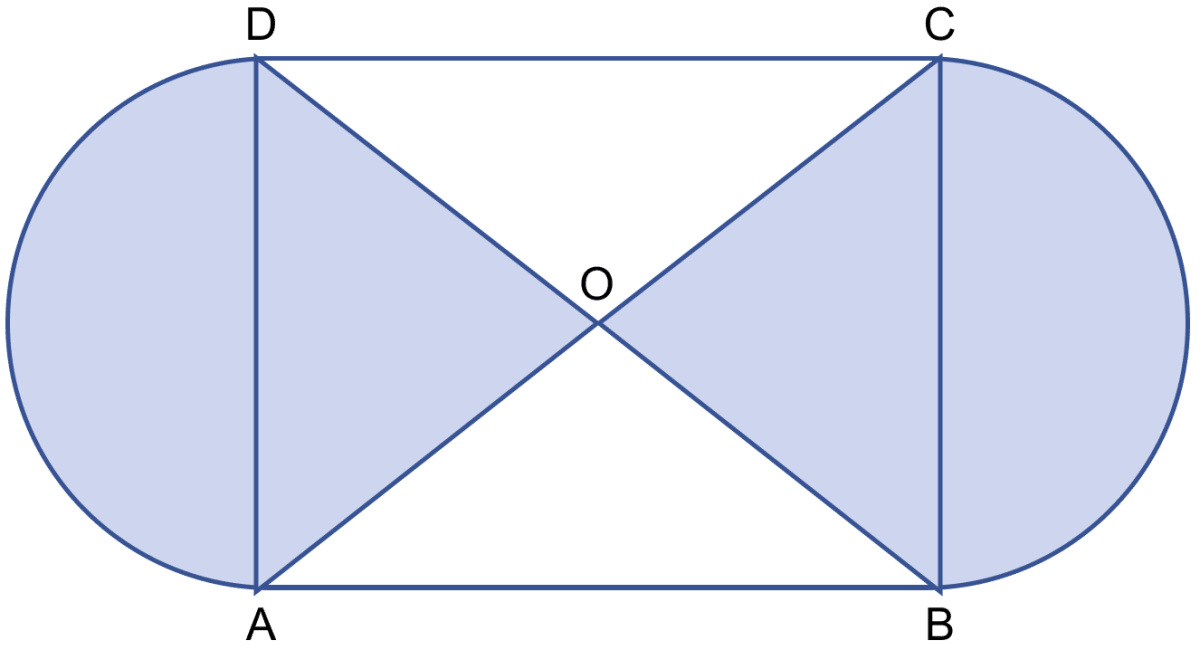
In the adjoining figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircle are drawn with AD and BC as diameters. Find the area of the shaded region. Take π = .
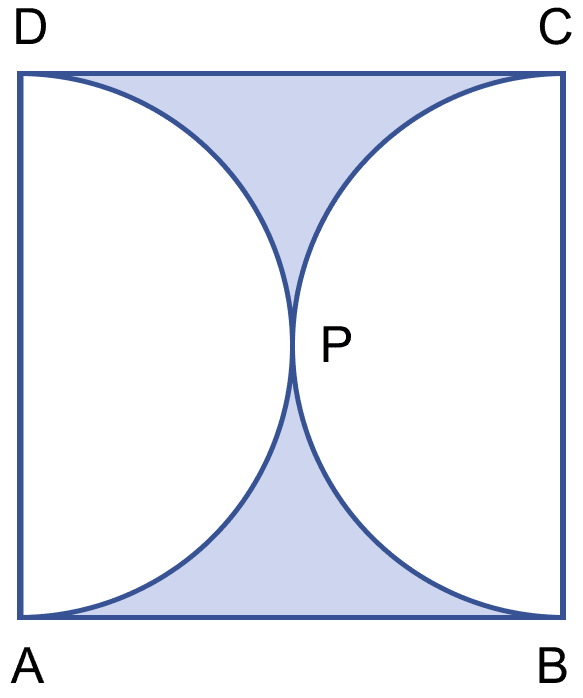
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.