Mathematics
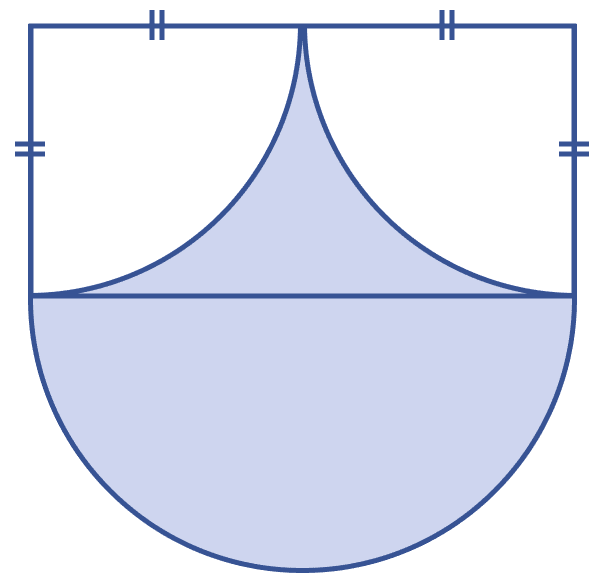
Find the area and the perimeter of the shaded region in figure (i) given below. The diamensions are in centimeters.

Mensuration
69 Likes
Answer
From figure,
Radius of larger semi-circle (R) = 14 cm.
Area of larger semi-circle =
= 22 × 14
= 308 cm2.
Diameter of smaller semi-circle = 14 cm; radius (r) = = 7 cm.
Area of smaller semi-circle =
= 11 × 7
= 77 cm2.
From figure,
Area of shaded region = Area of larger semi-circle - Area of smaller semi-circle
= 308 - 77
= 231 cm2.
From figure,
Perimeter of shaded region = Circumference of larger semi-circle + Circumference of smaller circle + 14
= πR + πr + 14
=
= 44 + 22 + 14
= 80 cm.
Hence, area of shaded region = 231 cm2 and perimeter = 80 cm.
Answered By
43 Likes
Related Questions
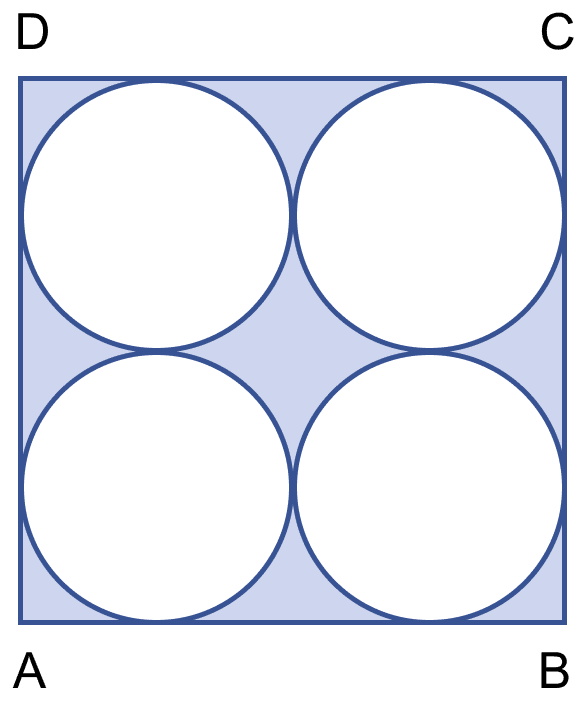
In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .
In the figure (ii) given below, area of △ABC = 35 cm2. Find the area of the shaded region.

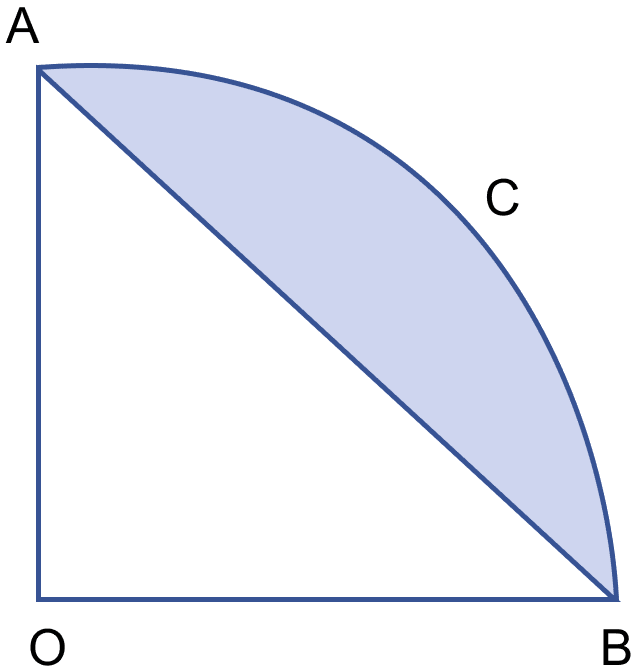
In the figure (i) given below, AOBC is a quadrant of a circle of radius 10 m. Calculate the area of the shaded portion. Take π = 3.14 and give your answer correct to two significant figures.