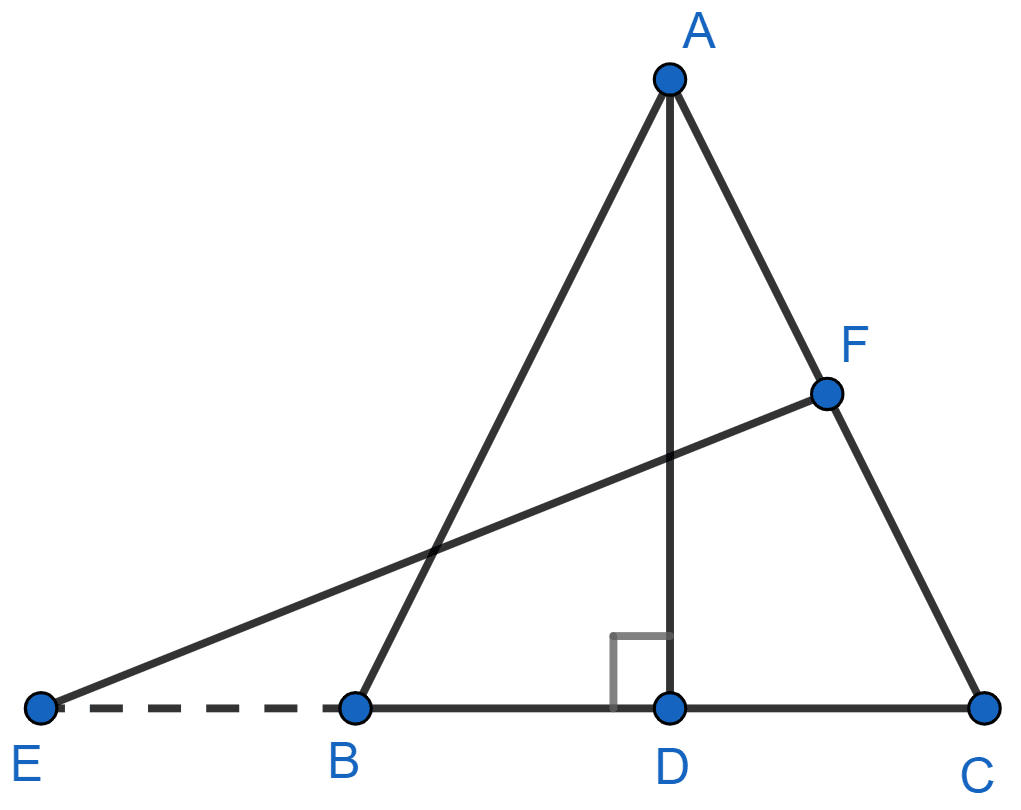
In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.

In Δ ABC,

AB = AC (Given)

∠ABC = ∠ACB (As angles opposite to equal sides are equal.) ……(1)

From figure,

∠ABD = ∠ABC and ∠ACB = ∠ECF

Substituting values of ∠ABC and ∠ACB in equation (1), we get :

⇒ ∠ABD = ∠ECF

In Δ ABD and Δ ECF,

⇒ ∠ADB = ∠EFC = 90° [∵ AD ⊥ BC and EF ⊥ AC]

⇒ ∠ABD = ∠ECF [Proved above]

∴ Δ ABD ~ Δ ECF (By A.A. axiom)

Hence, proved that Δ ABD ~ Δ ECF.