Mathematics
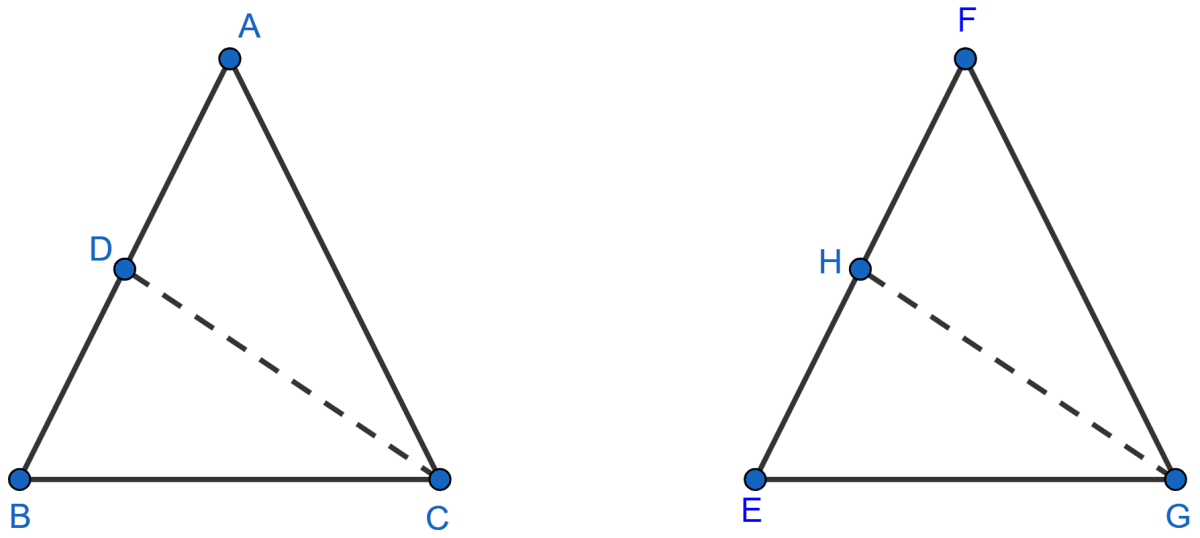
CD and GH are respectively the bisectors of Δ ACB and Δ EGF such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
Triangles
4 Likes
Answer
(i) Given,
∆ ABC ~ ∆ FEG
We know that,
If two triangles are similar, then their corresponding angles are congruent.
⇒ ∠ACB = ∠FGE
⇒
⇒ ∠ACD = ∠FGH (CD and GH are bisectors of ∠C and ∠G respectively) …………..(1)
In ∆ ADC and ∆ FHG,
⇒ ∠DAC = ∠HFG [∵ ∆ABC ~ ∆FEG]
⇒ ∠ACD = ∠FGH [From equation (1)]
∴ ∆ ADC ~ ∆ FHG (By A.A. axiom)
We know that,
Ratio of corresponding sides in similar triangle are proportional.
∴ .
Hence, proved that .
(ii) In ∆ DCB and ∆ HGE,
⇒ ∠DBC = ∠HEG [∵ ∆ ABC ~ ∆ FEG]
⇒ ∠DCB = ∠HGE [∵ ]
∴ ∆ DCB ~ ∆ HGE (By A.A. axiom)
Hence, proved that ∆ DCB ~ ∆ HGE.
(iii) In ∆ DCA and ∆ HGF,
⇒ ∠DAC = ∠HFG [∆ ABC ~ ∆ FEG]
⇒ ∠ACD = ∠FGH [From (1)]
∴ ∆ DCA ~ ∆ HGF (By A.A. axiom)
Hence, proved that ∆ DCA ~ ∆ HGF.
Answered By
3 Likes
Related Questions
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that △ ABE ~ △ CFB.
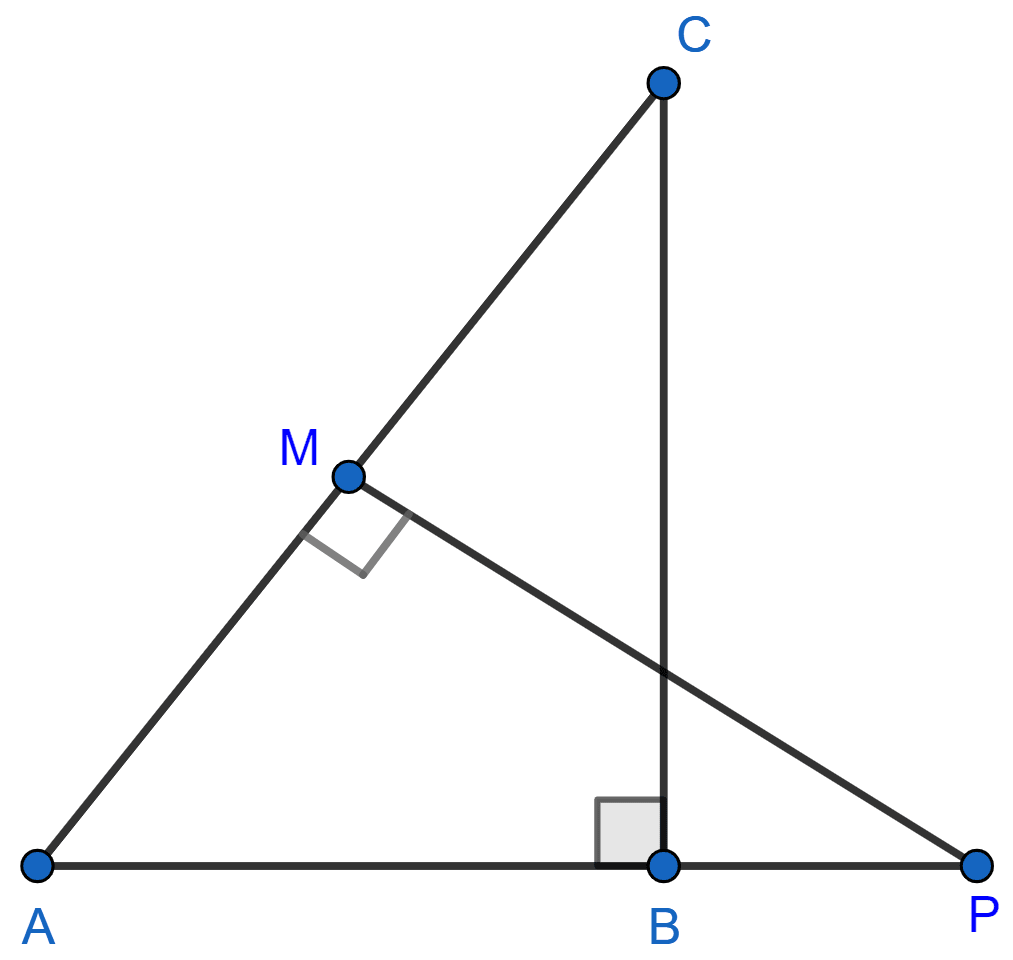
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
(i) Δ ABC ~ Δ AMP
(ii)
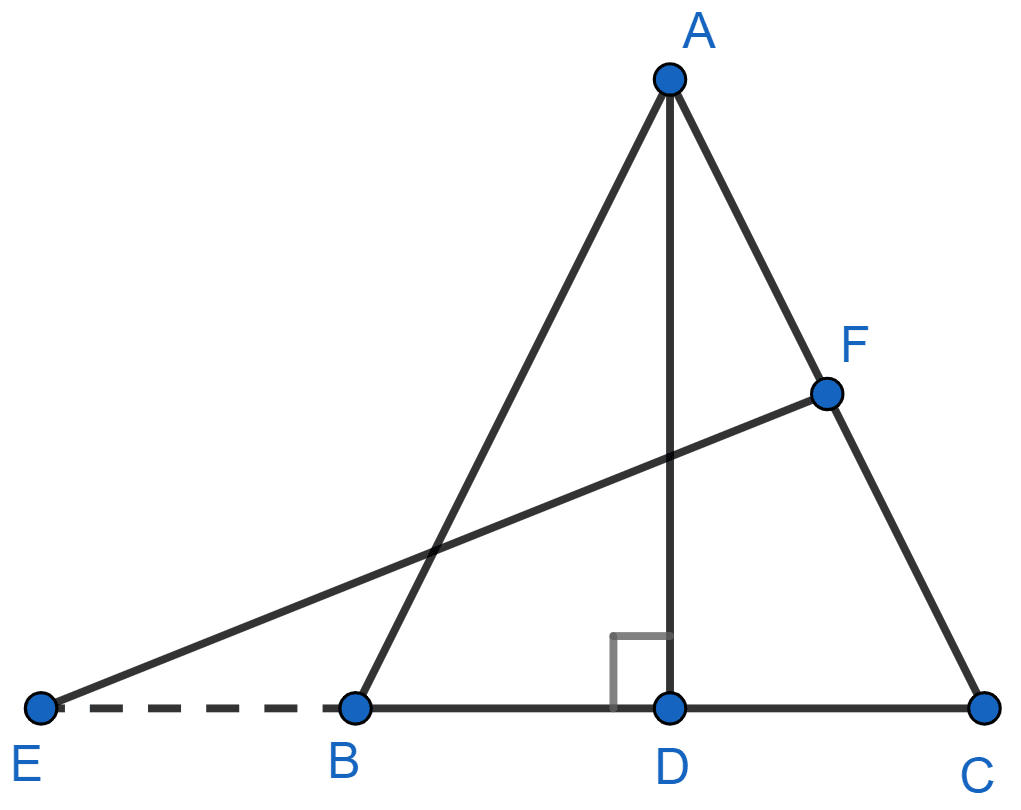
In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.
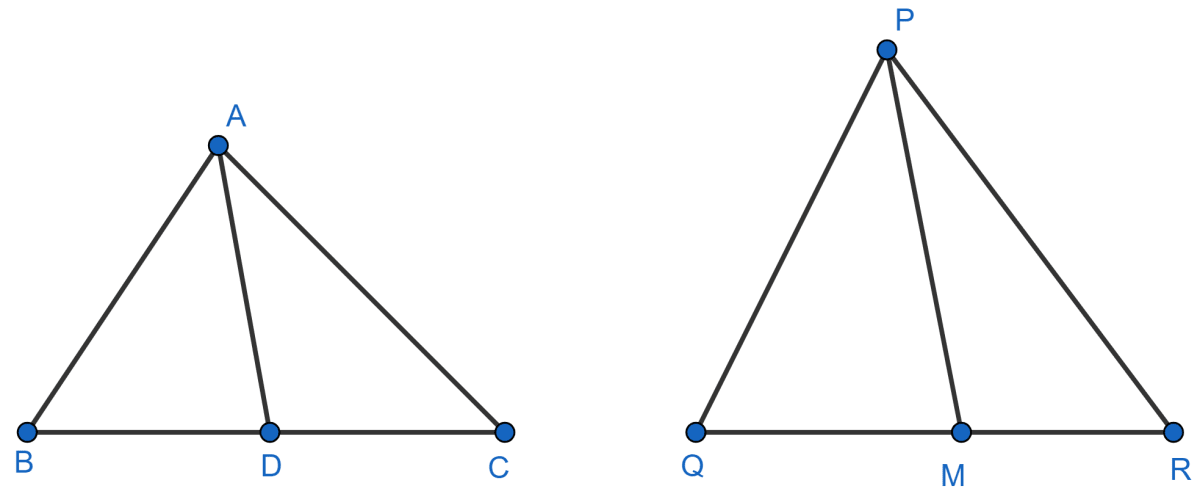
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR. Show that △ ABC ~ △ PQR.