Mathematics
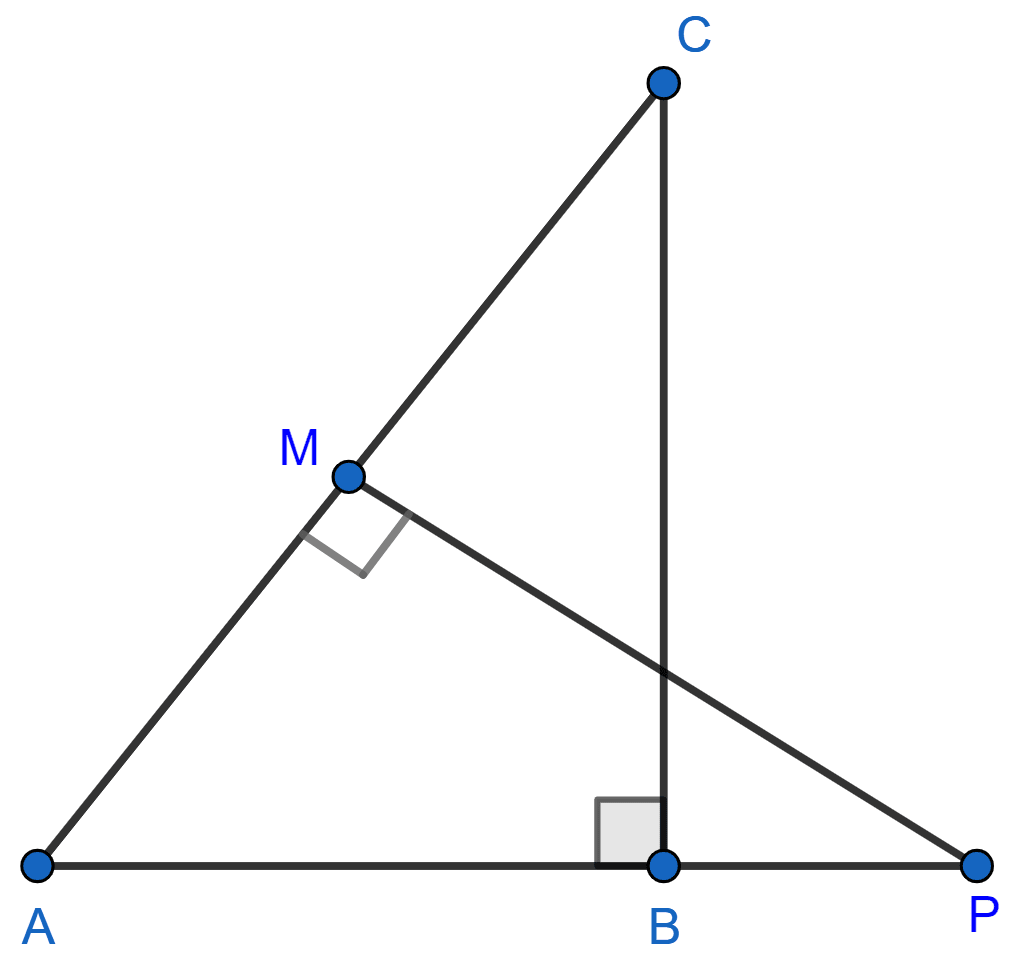
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
(i) Δ ABC ~ Δ AMP
(ii)
Triangles
1 Like
Answer
(i) In Δ ABC and Δ AMP,
⇒ ∠ABC = ∠AMP (Both = 90°)
⇒ ∠BAC = ∠MAP (Common angle)
∴ Δ ABC ∼ Δ AMP (By A.A. axiom)
Hence, proved that Δ ABC ~ Δ AMP.
(ii) We know that,
Ratio of corresponding sides in two similar triangles are proportional.
In Δ ABC and Δ AMP,
Hence, proved that .
Answered By
1 Like
Related Questions
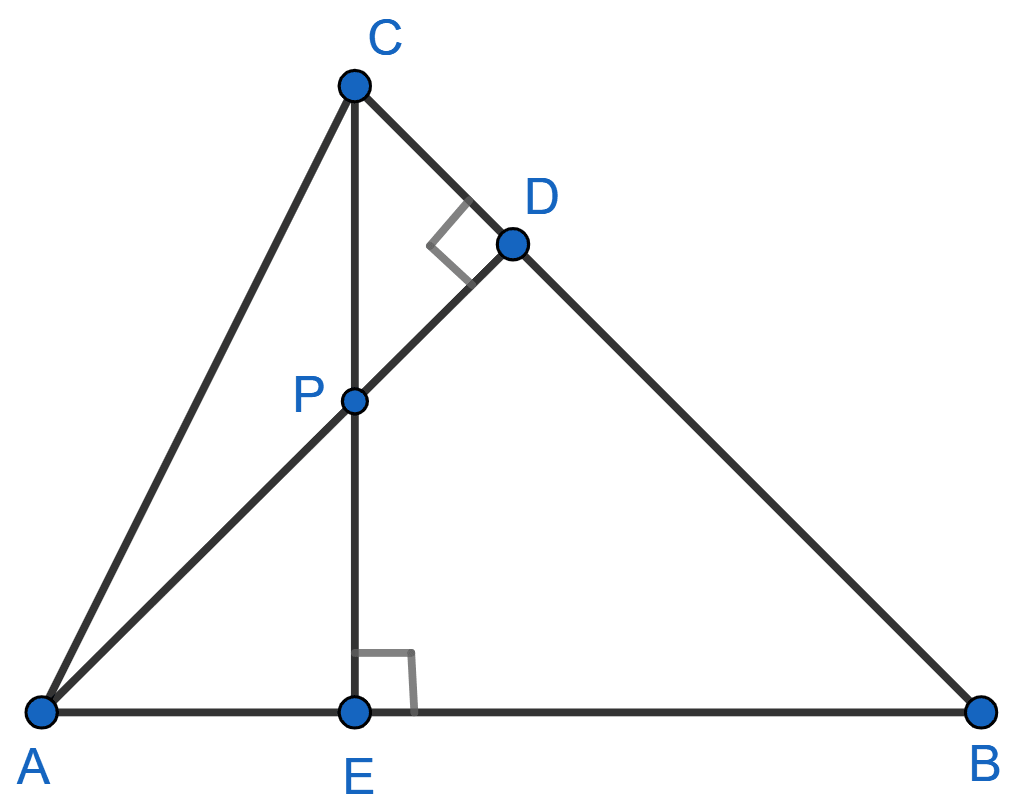
In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i) ∆ AEP ~ ∆ CDP
(ii) ∆ ABD ~ ∆ CBE
(iii) ∆ AEP ~ ∆ ADB
(iv) ∆ PDC ~ ∆ BEC
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that △ ABE ~ △ CFB.
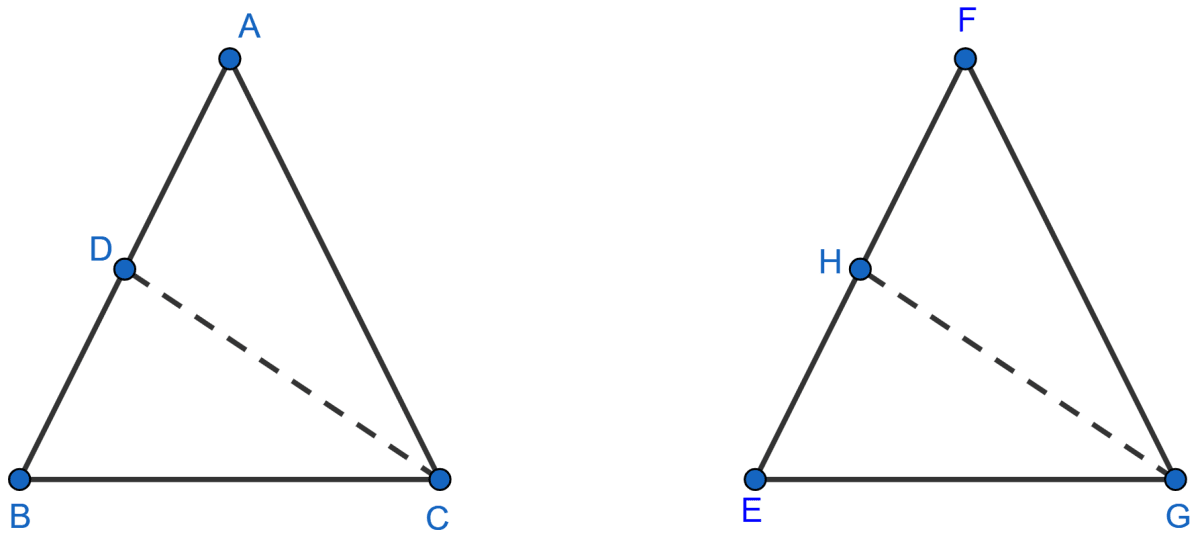
CD and GH are respectively the bisectors of Δ ACB and Δ EGF such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
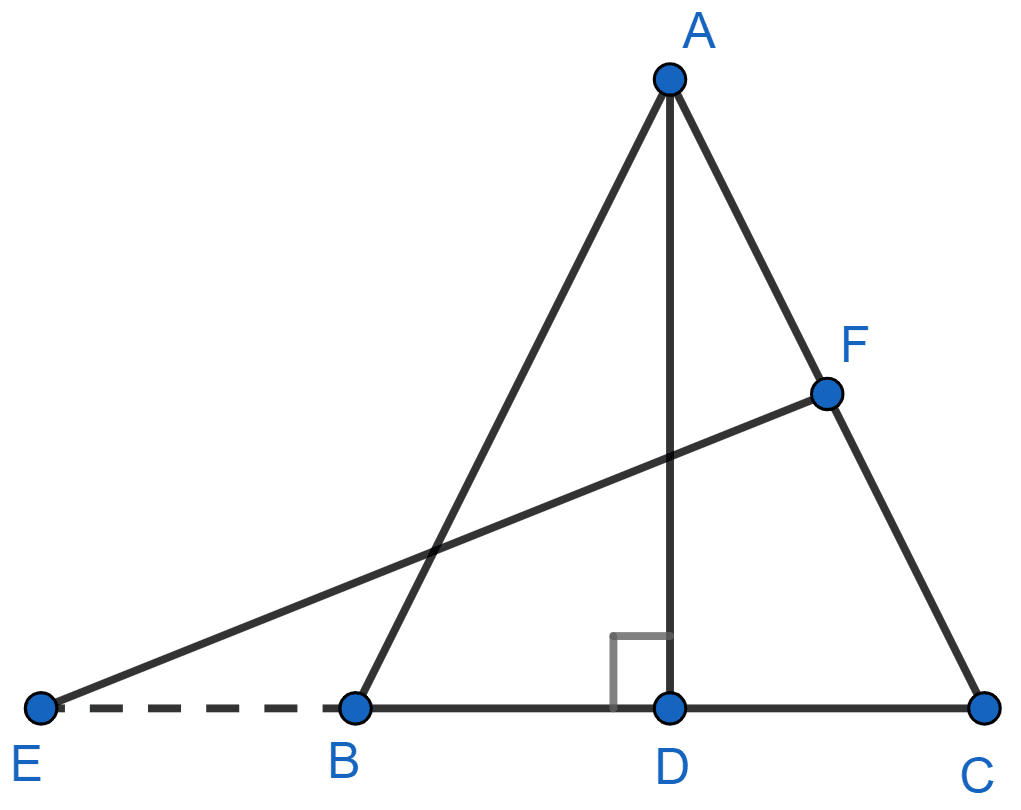
In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.