Mathematics
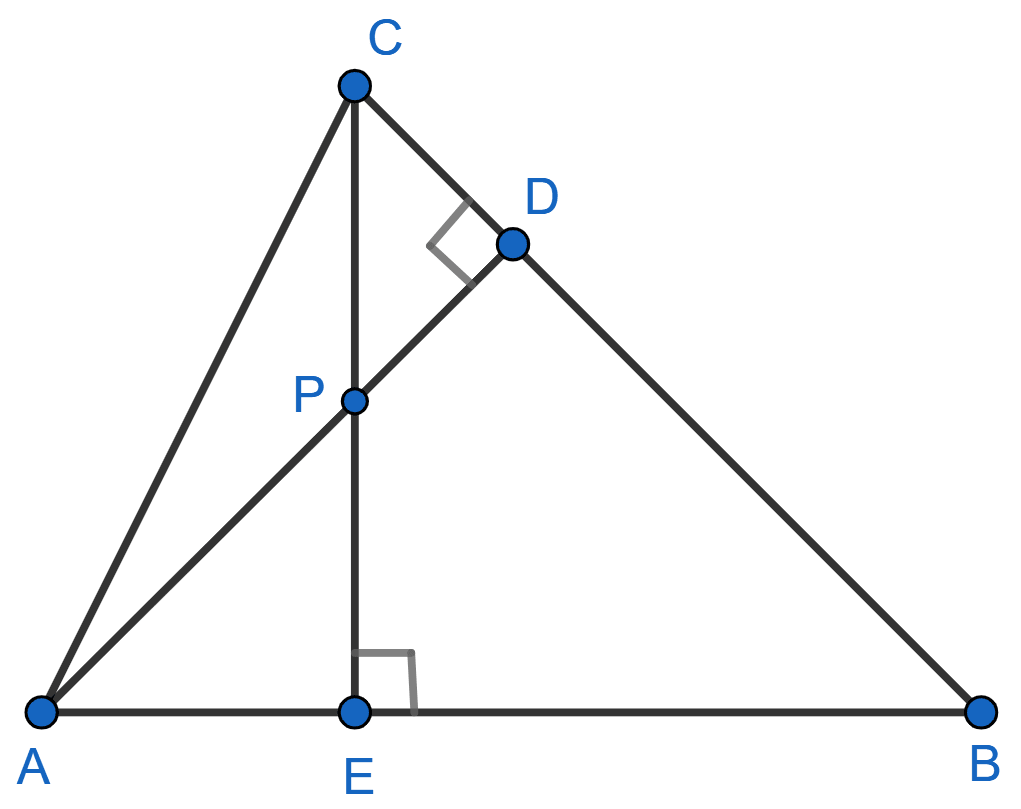
In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i) ∆ AEP ~ ∆ CDP
(ii) ∆ ABD ~ ∆ CBE
(iii) ∆ AEP ~ ∆ ADB
(iv) ∆ PDC ~ ∆ BEC
Triangles
4 Likes
Answer
(i) In Δ AEP and Δ CDP,
⇒ ∠AEP = ∠CDP (Both = 90°)
⇒ ∠APE = ∠CPD (Vertically opposite angles are equal)
⇒ Δ AEP ~ Δ CDP (By A.A. axiom)
Hence, proved that Δ AEP ~ Δ CDP.
(ii) In Δ ABD and Δ CBE,
⇒ ∠ADB = ∠CEB (Both = 90°)
⇒ ∠ABD = ∠CBE (Common angle)
⇒ Δ ABD ~ Δ CBE (By A.A. axiom)
Hence, proved that Δ ABD ~ Δ CBE.
(iii) In Δ AEP and Δ ADB,
⇒ ∠AEP = ∠ADB (Both = 90°)
⇒ ∠PAE = ∠BAD (Common angle)
⇒ Δ AEP ~ Δ ADB (By A.A. axiom)
Hence, proved that Δ AEP ~ Δ ADB.
(iv) In Δ PDC and Δ BEC,
⇒ ∠PDC = ∠BEC (Both = 90°)
⇒ ∠PCD = ∠BCE (Common angle)
⇒ Δ PDC ~ Δ BEC (By A.A. axiom)
Hence, proved that Δ PDC ~ Δ BEC.
Answered By
2 Likes
Related Questions
S and T are points on sides PR and QR of △ PQR such that ∠P = ∠RTS. Show that △ RPQ ~ △ RTS.
In given figure, if △ ABE ≅ Δ ACD, show that
△ ADE ∼ Δ ABC.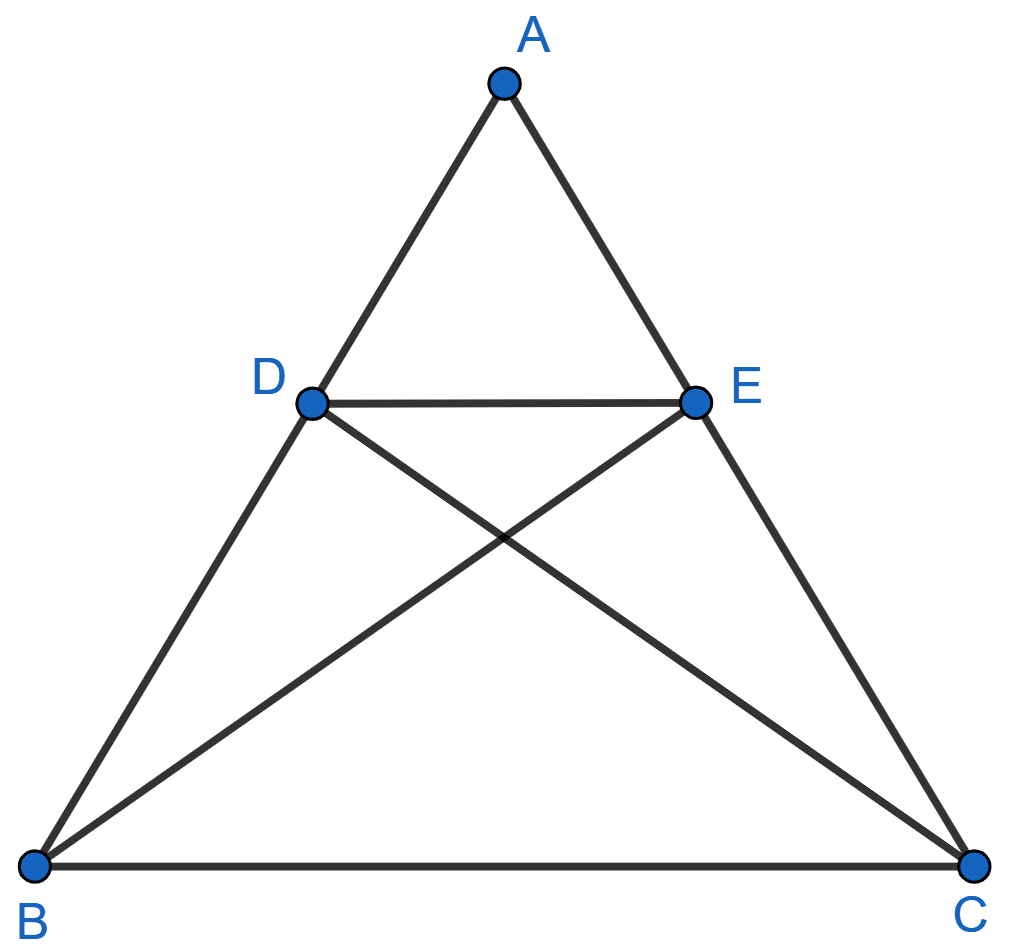
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that △ ABE ~ △ CFB.
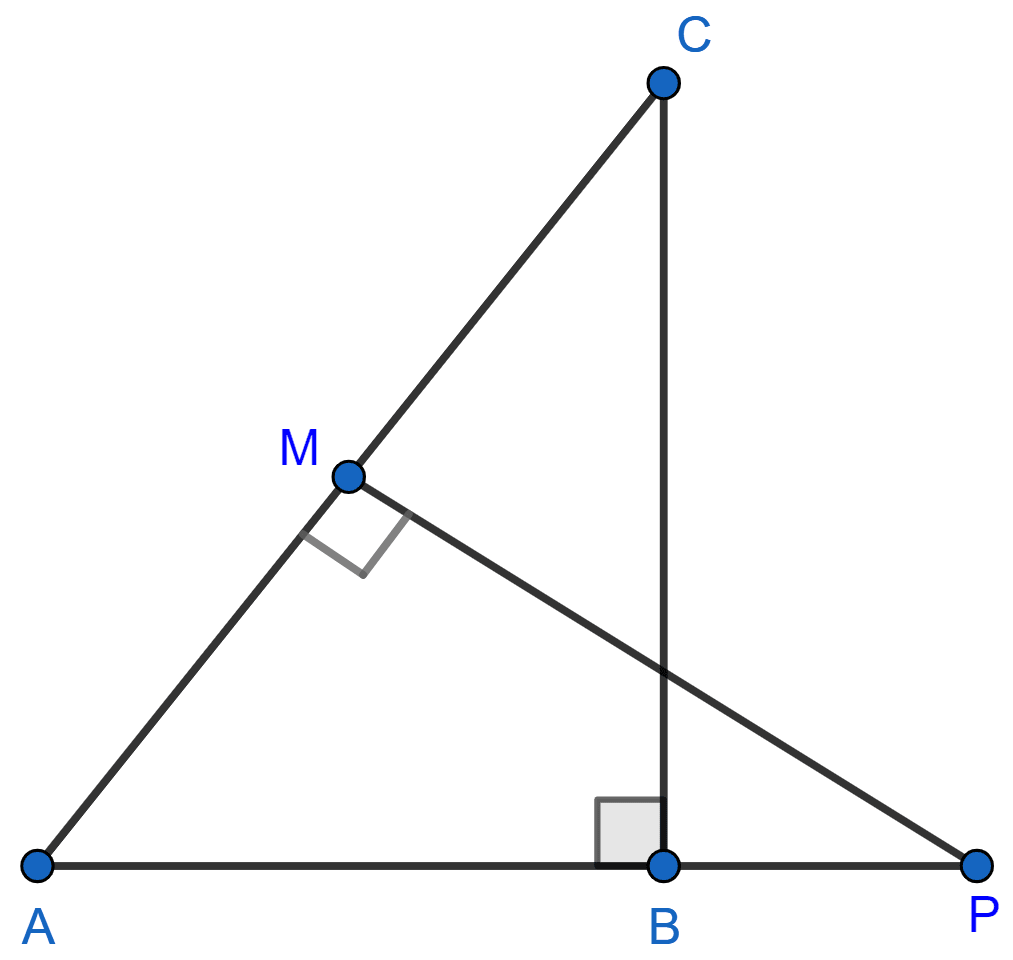
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
(i) Δ ABC ~ Δ AMP
(ii)