Mathematics
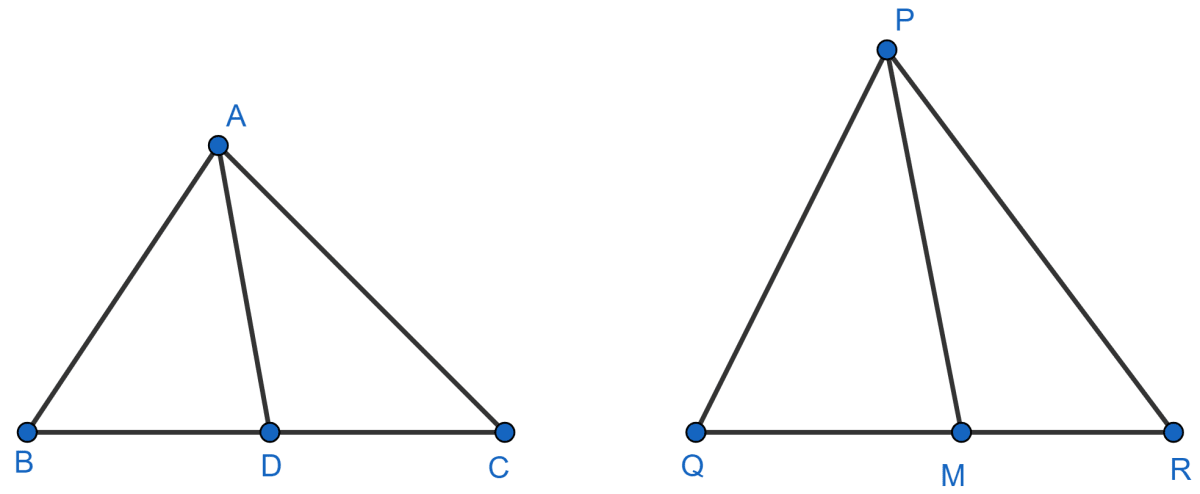
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR. Show that △ ABC ~ △ PQR.
Triangles
2 Likes
Answer
In Δ ABC and Δ PQR,
As, sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR.
…….(1)
AD and PM are median of Δ ABC and Δ PQR respectively.
Substituting value of from above equation in (1), we get :
⇒
∴ Δ ABD ∼ Δ PQM [By SSS axiom]
In Δ ABC and Δ PQR,
⇒ [Given]
⇒ ∠ABC = ∠PQR [∵ Δ ABD ∼ Δ PQM]
∴ Δ ABC ∼ Δ PQR [By S.A.S. axiom]
Hence, proved that Δ ABC ∼ Δ PQR.
Answered By
1 Like
Related Questions
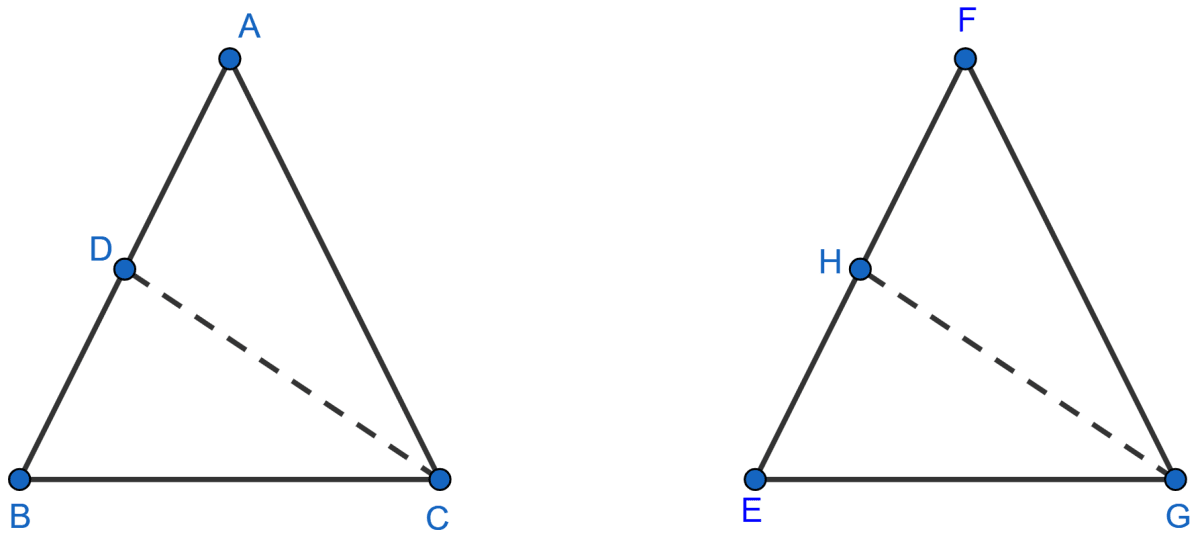
CD and GH are respectively the bisectors of Δ ACB and Δ EGF such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
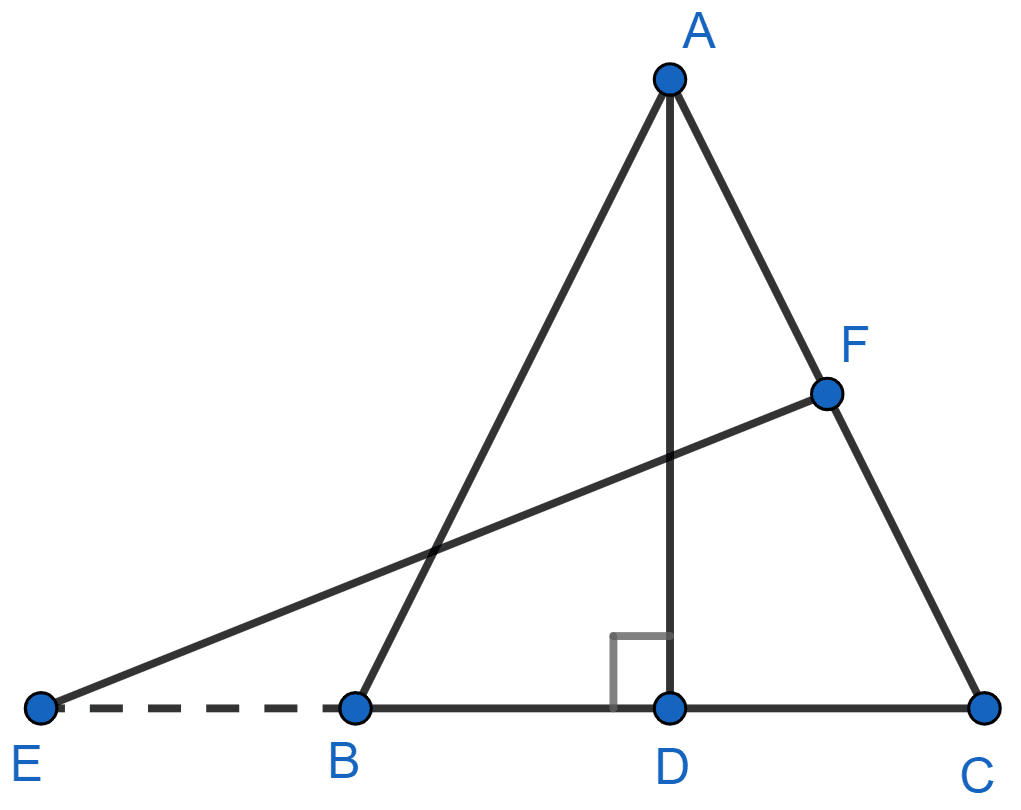
In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.