Mathematics
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Triangles
3 Likes
Answer
Δ ABC is shown in the figure below:
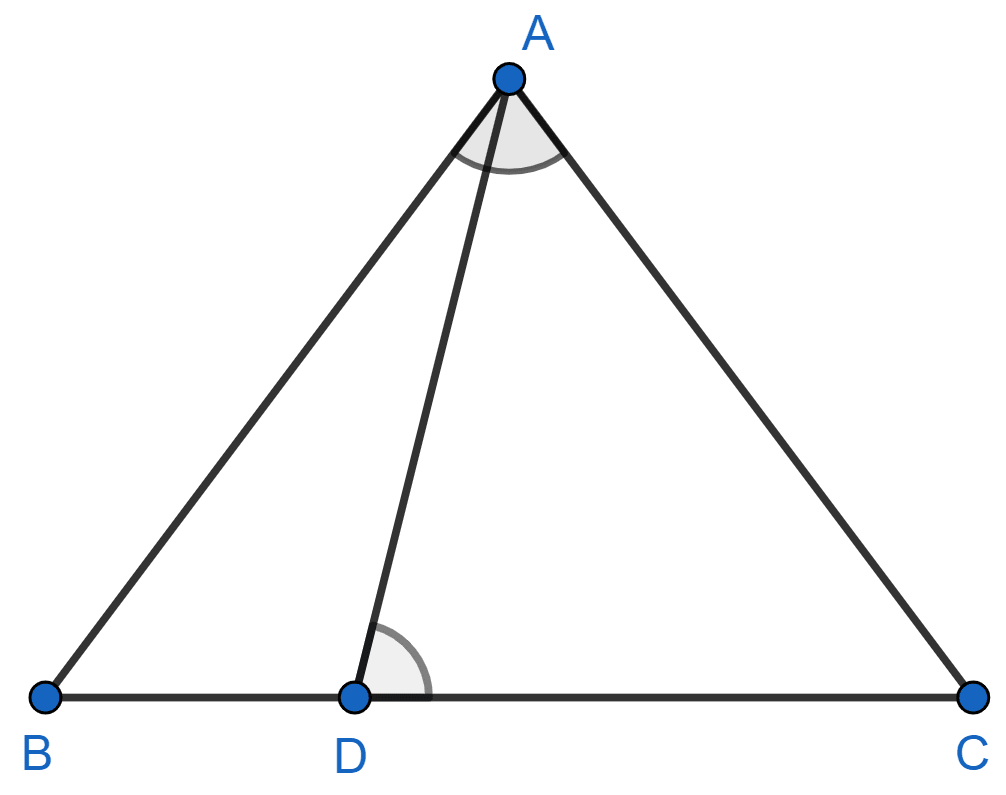
In Δ ABC and Δ DAC,
⇒ ∠BAC = ∠ADC (Given)
⇒ ∠ACB = ∠ACD (Common angles)
∴ Δ ABC ∼ Δ DAC (By A.A. axiom)
We know that,
Corresponding sides of similar triangle are proportional.
⇒ CA2 = CB × CD.
Hence, proved that CA2 = CB × CD.
Answered By
2 Likes
Related Questions
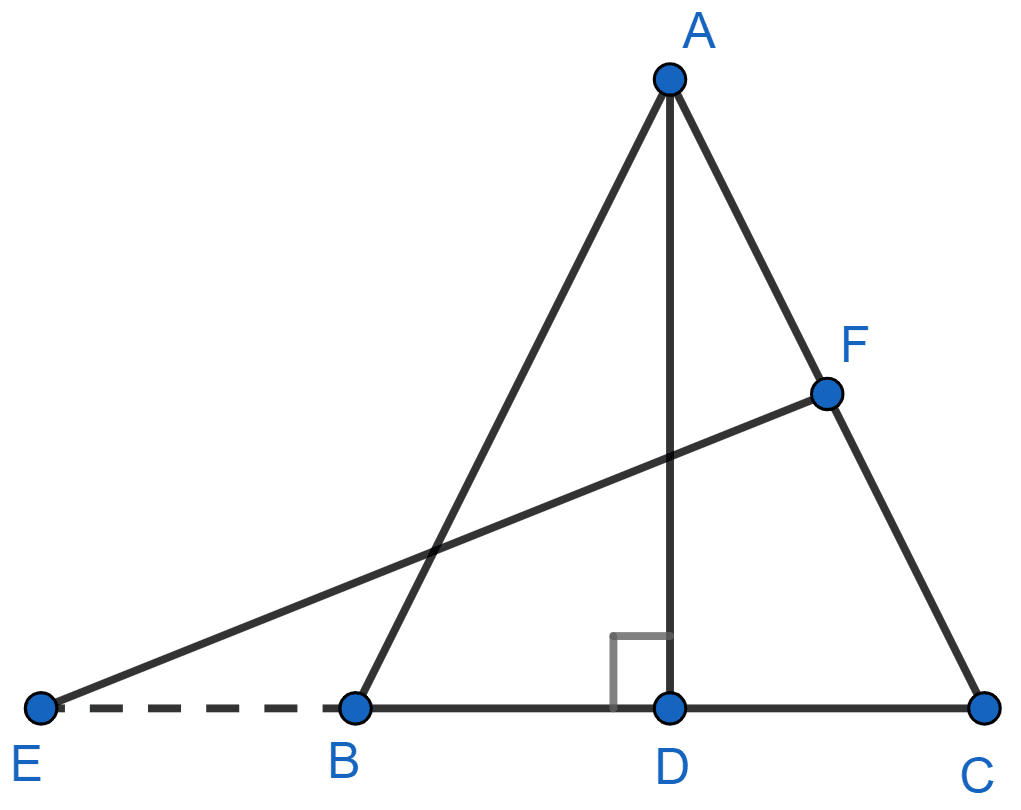
In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR. Show that △ ABC ~ △ PQR.
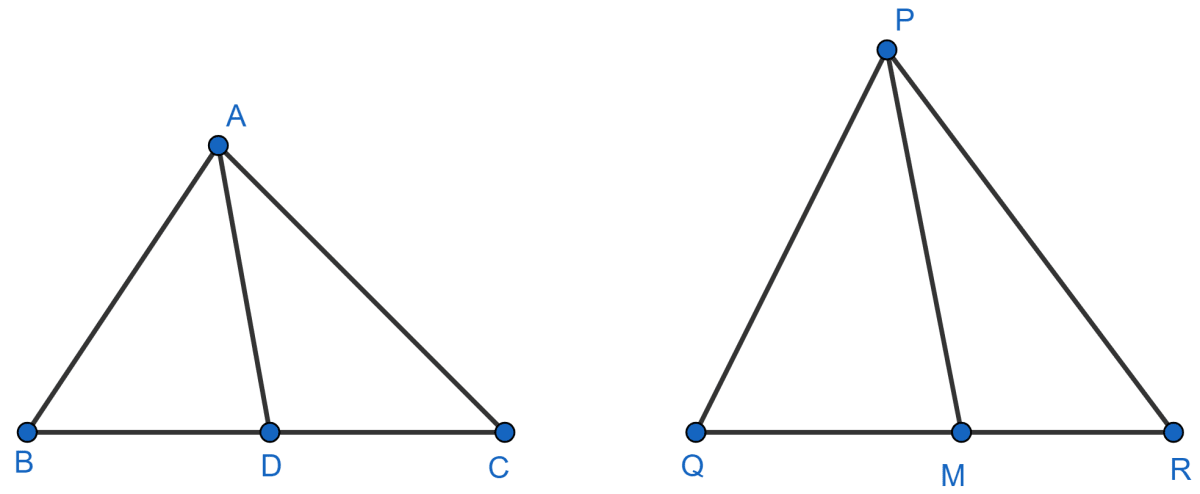
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.