A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Let AB be the pole of length 6 m and BC = 4 m is the shadow of pole AB.

Let PQ be the tower and QR = 28 m is the shadow of the tower PQ.

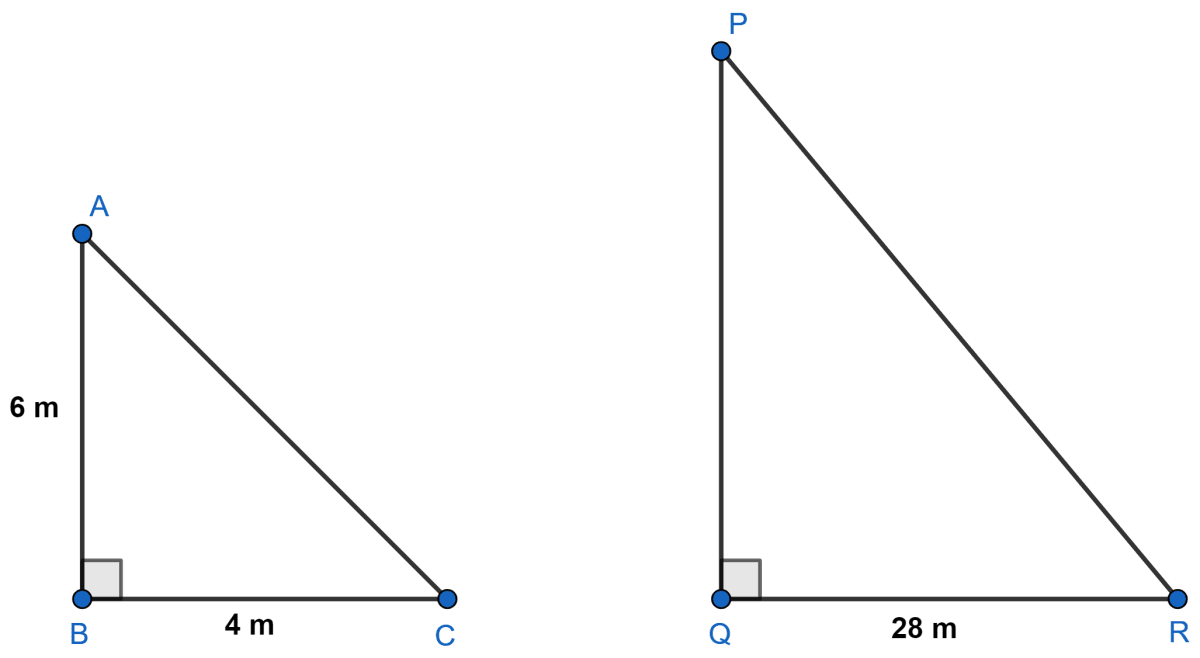
In Δ ABC and Δ PQR,

⇒ ∠ABC = ∠PQR (Both equal to 90°.)

⇒ ∠BAC = ∠QPR (Sunray falls on the pole and tower at the same angle, at the same time)

⇒ Δ ABC ∼ Δ PQR (By A.A. axiom)

We know that,

If two triangles are similar then their corresponding sides are proportional.

$\Rightarrow \dfrac{AB}{PQ} = \dfrac{BC}{QR} \\[1em] \Rightarrow PQ = \dfrac{AB \times QR}{BC} \\[1em] \Rightarrow PQ = \dfrac{6 \times 28}{4} \\[1em] \Rightarrow PQ = 42 \text{ m}.$

Hence, the height of the tower is 42 m.