Mathematics
In the figure (1) given below, ABCD is a rectangle (not drawn to scale) with side AB = 4 cm and AD = 6 cm. Find
(i) the area of parallelogram DEFC
(ii) area of △EFG.

Theorems on Area
11 Likes
Answer
(i) We know that,
A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
From figure,
rectangle ABCD and parallelogram DEFC are on the same base DC and between same parallel lines DG and AF.
Hence, area of || gm DEFC = area of rectangle ABCD
= AB × AD
= 4 × 6
= 24 cm2.
Hence, area of || gm DEFC = 24 cm2.
(ii) We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallel lines.
Since, triangle GEF and || gm DEFC are on same base EF and between same parallel lines DG and AF so,
area of △EFG = area of || gm DEFC
= cm2.
Hence, area of △EFG = 12 cm2.
Answered By
7 Likes
Related Questions
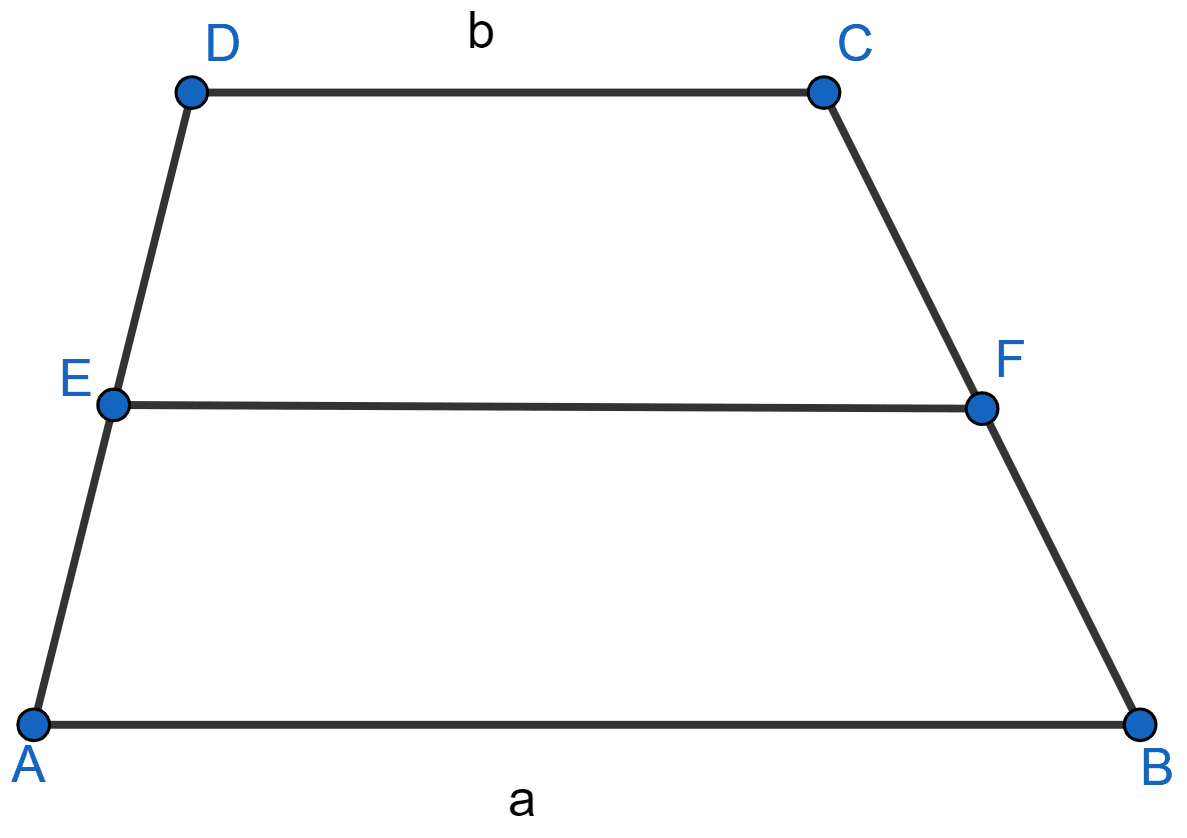
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC
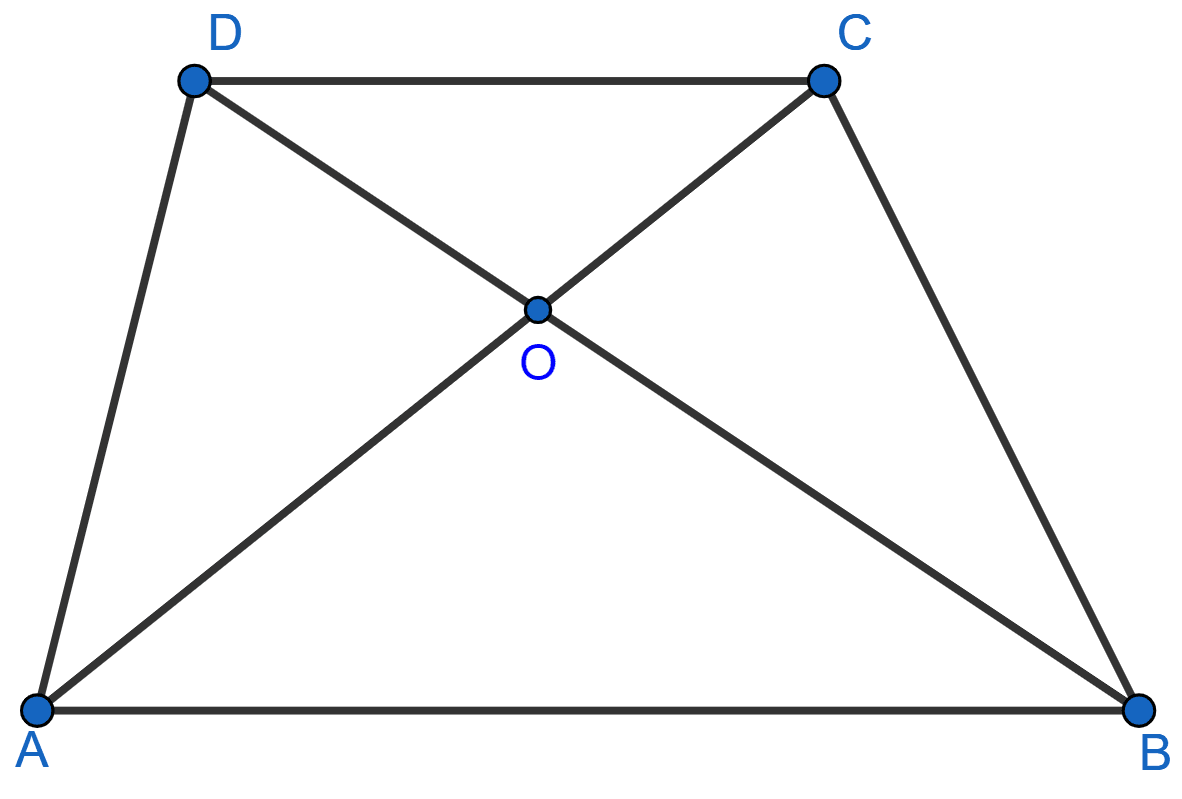
In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 × area of quad. ABCD.
In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii) area of ∆ADQ = area of ∆APD + area of ∆CPB.