Mathematics
In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii) area of ∆ADQ = area of ∆APD + area of ∆CPB.
Theorems on Area
10 Likes
Answer
Parallelogram ABCD with point P on the side AB and Q on the side BC is shown below:

∆CPD and || gm ABCD are on the same base CD and between the same parallels lines AB and CD.
∴ Area of ∆CPD = Area of || gm ABCD ……(1)
∆AQD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC,
∴ Area of ∆AQD = Area of || gm ABCD …….(2)
From (1) and (2),
Area of ∆CPD = Area of ∆AQD.
Hence, proved that area of ∆CPD = area of ∆AQD.
(ii) From part (i) we get,
Area of ∆CPD = Area of || gm ABCD
∴ Area of || gm ABCD - Area of ∆CPD = Area of || gm ABCD ……..(3)
From figure,
Area of || gm ABCD - Area of ∆CPD = Area of ∆APD + Area of ∆CPB ………(4)
From (3) and (4) we get,
⇒ Area of ∆APD + Area of ∆CPB = Area of || gm ABCD
Since,
Area of ∆ADQ = Area of || gm ABCD (From eq 2)
⇒ Area of ∆APD + Area of ∆CPB = Area of ∆ADQ.
Hence, proved that area of ∆ADQ = area of ∆APD + area of ∆CPB.
Answered By
8 Likes
Related Questions
In the figure (1) given below, ABCD is a rectangle (not drawn to scale) with side AB = 4 cm and AD = 6 cm. Find
(i) the area of parallelogram DEFC
(ii) area of △EFG.

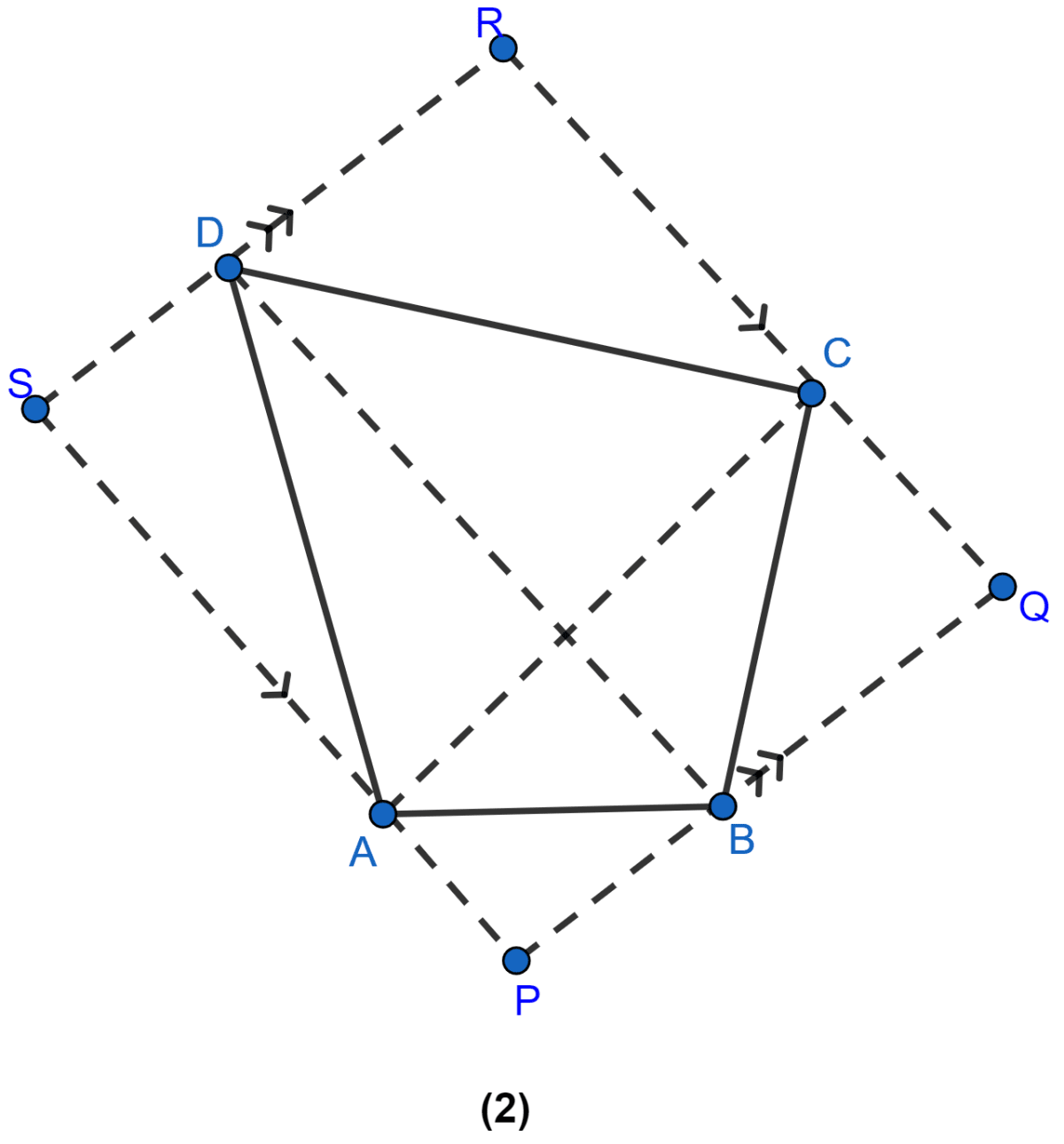
In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 × area of quad. ABCD.
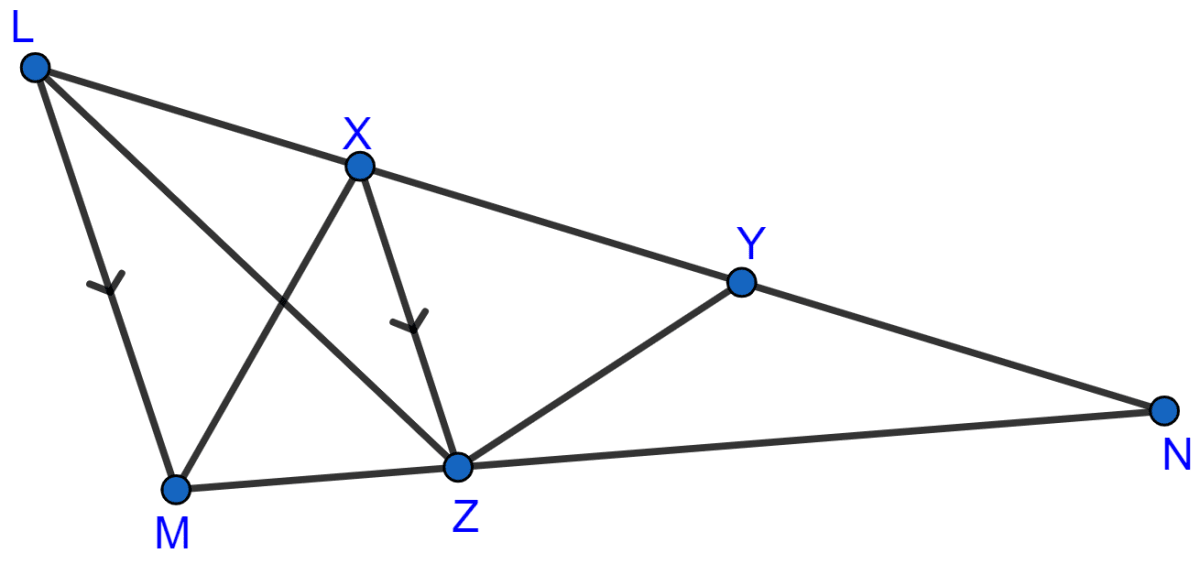
In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.