Mathematics
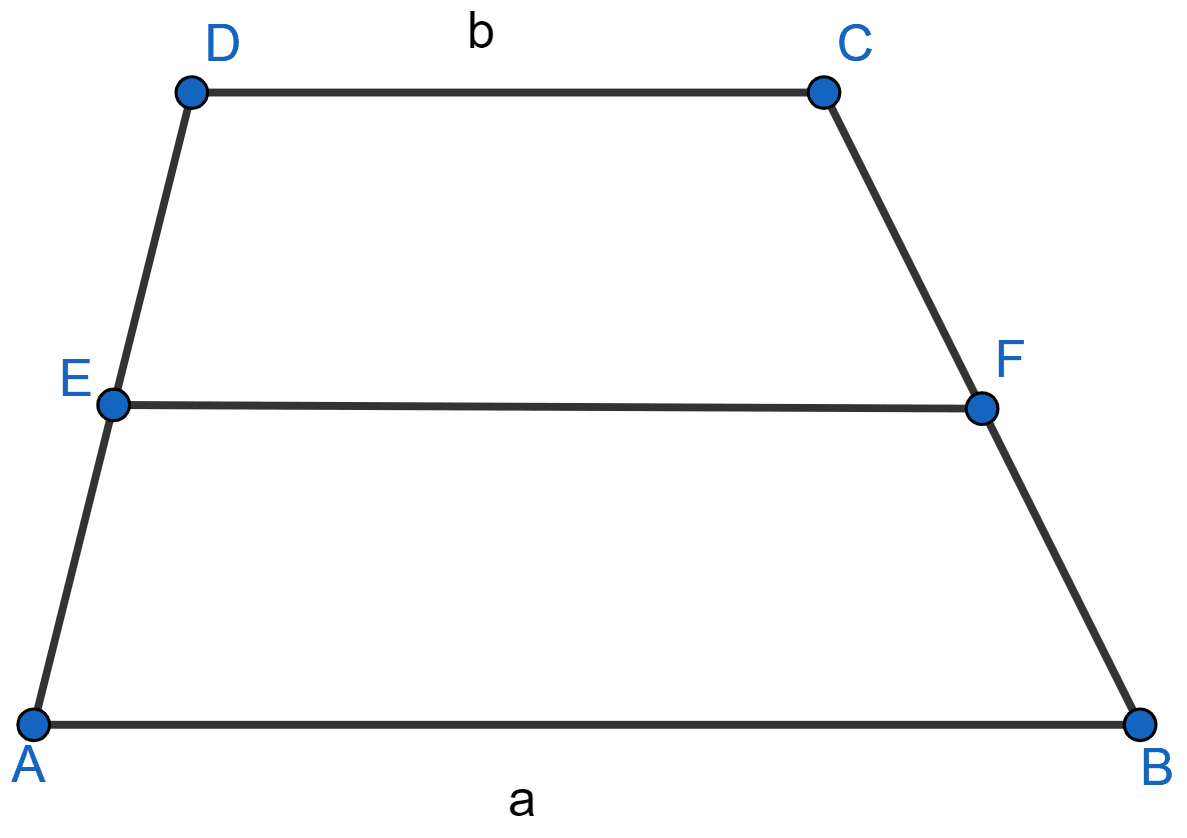
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
Theorems on Area
4 Likes
Answer
It is given that
AB = a cm
DC = b cm
AB || DC
E and F are the mid-points of AD and BC
Consider h as the distance between AB, CD and EF
Now join BD which intersects EF at M
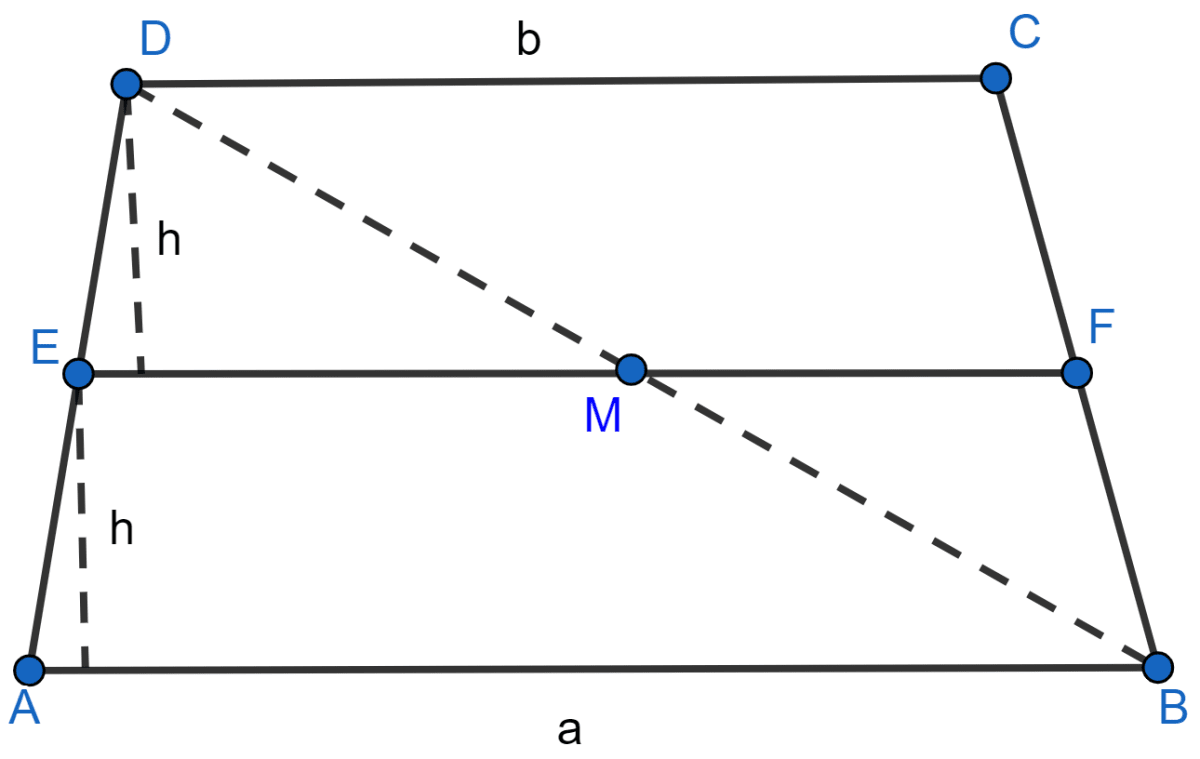
In ∆ABD,
E is the midpoint of AD and EM || AB
By midpoint theorem,
M is the midpoint of BD
and
EM = AB …….. (1)
In ∆CBD,
F is mid-point of BC and M is mid-point of BD so by mid-point theorem,
MF = CD ……… (2)
Adding equations (1) and (2)
EM + MF = AB + CD
EF = (AB + CD)
EF = (a + b)
Here,
Area of trapezium ABFE = [sum of parallel sides] × [distance between parallel sides]
Substituting the values,
Similarly,
Required ratio = Area of trapezium ABFE / Area of trapezium EFCD
By substituting the values,
Hence, Option 2 is the correct option.
Answered By
4 Likes
Related Questions
In the adjoining figure, area of parallelogram ABCD is
AB × BM
BC × BN
DC × DL
AD × DL

The mid-points of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
area of △ABC
area of △ABC
area of △ABC
area of △ABC
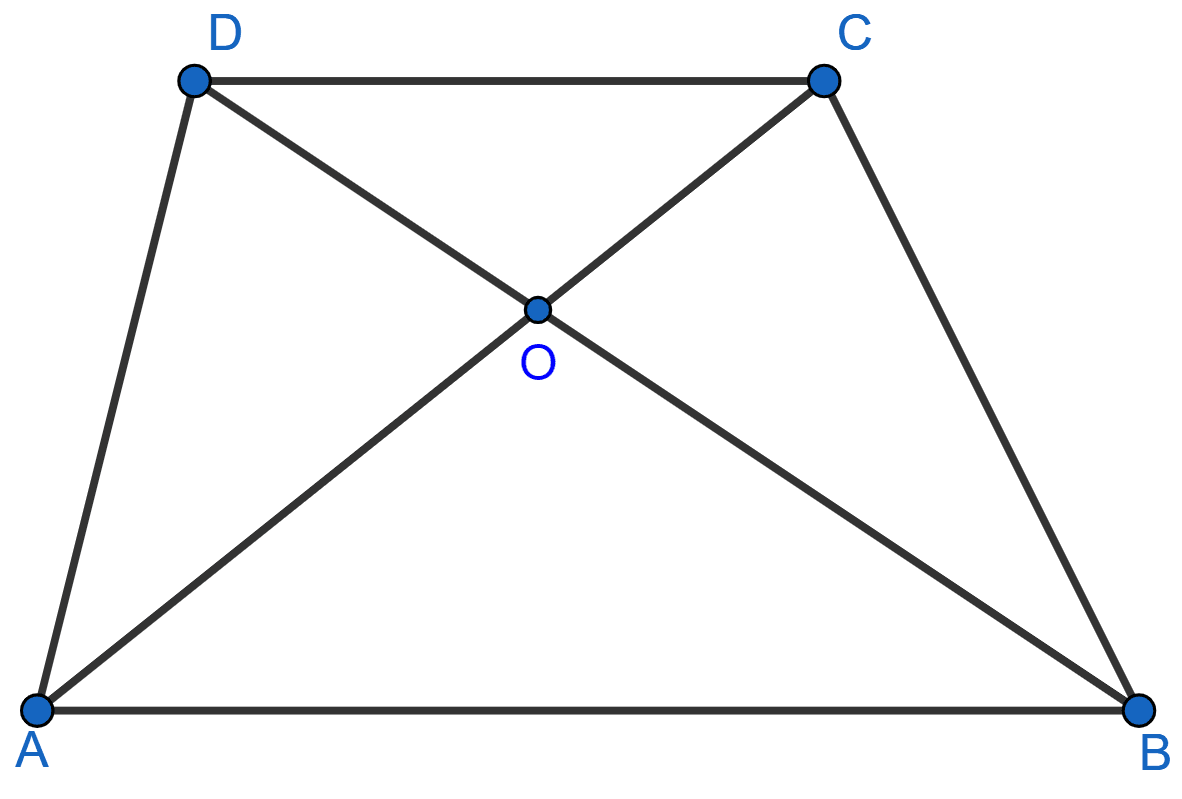
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC
In the figure (1) given below, ABCD is a rectangle (not drawn to scale) with side AB = 4 cm and AD = 6 cm. Find
(i) the area of parallelogram DEFC
(ii) area of △EFG.
