Mathematics
The mid-points of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
area of △ABC
area of △ABC
area of △ABC
area of △ABC
Theorems on Area
1 Like
Answer
Let CDEF be a parallelogram.
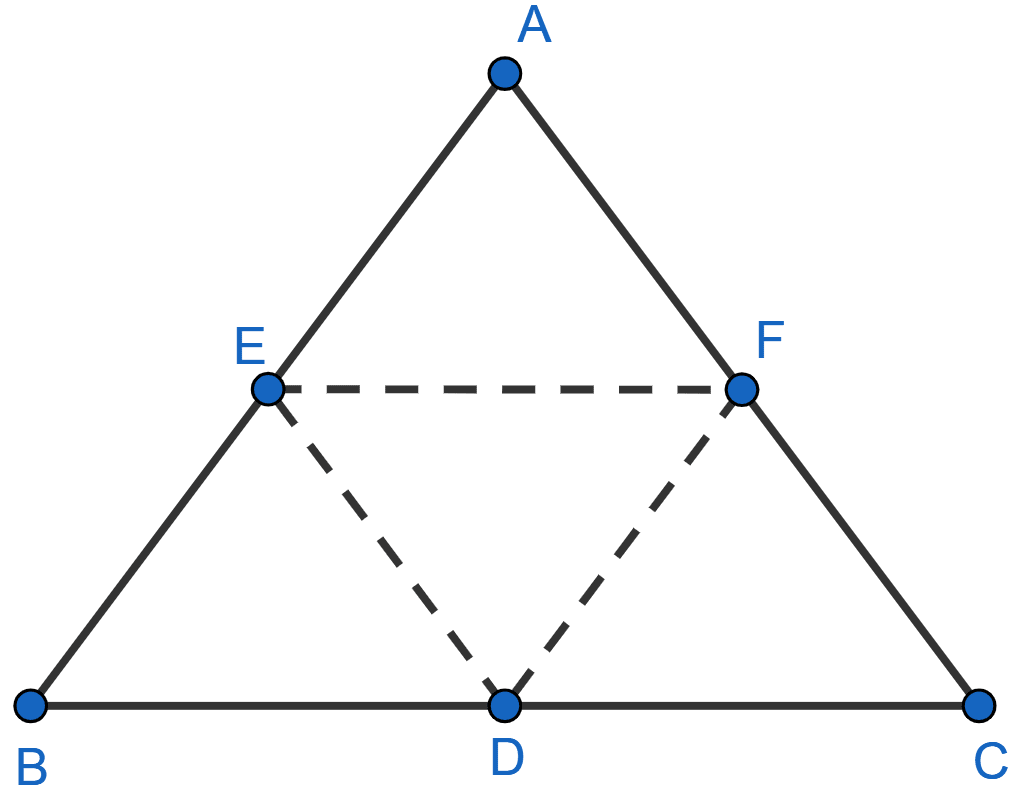
So, diagonal DF divides it into two triangles of equal area.
∴ area of △CDF = area of △EDF ……..(i)
E and F are mid-points of side AB and AC respectively.
By mid-point theorem,
EF = BC = BD (As D is mid-point of BC) and EF || BC.
Since, FE || BC so from figure,
EF || BD and EF = BD.
So, EBDF is a paralleogram with diagonal ED dividing it into two triangles of equal area.
∴ area of △EBD = area of △EDF ……..(ii)
E and D are mid-points of side AB and BC respectively.
By mid-point theorem,
ED = AC = AF (As F is mid-point of AC) and ED || AC.
Since, ED || AC so from figure,
ED || AF.
So, AEDF is a paralleogram with diagonal EF dividing it into two triangles of equal area.
∴ area of △AEF = area of △EDF ……..(iii)
From (i), (ii) and (iii) we get,
area of △EDF = area of △CDF = area of △EBD = area of △AEF = x
From figure,
area of △ABC = area of △EDF + area of △CDF + area of △EBD + area of △AEF = 4x.
area of || gm EDCF = area of △EDF + area of △CDF = 2x.
So,
area of || gm EDCF = area of △ABC.
Hence, Option 1 is the correct option.
Answered By
1 Like
Related Questions
A median of a triangle divides it into two
triangles of equal area
congruent triangles
right triangles
isosceles triangles
In the adjoining figure, area of parallelogram ABCD is
AB × BM
BC × BN
DC × DL
AD × DL

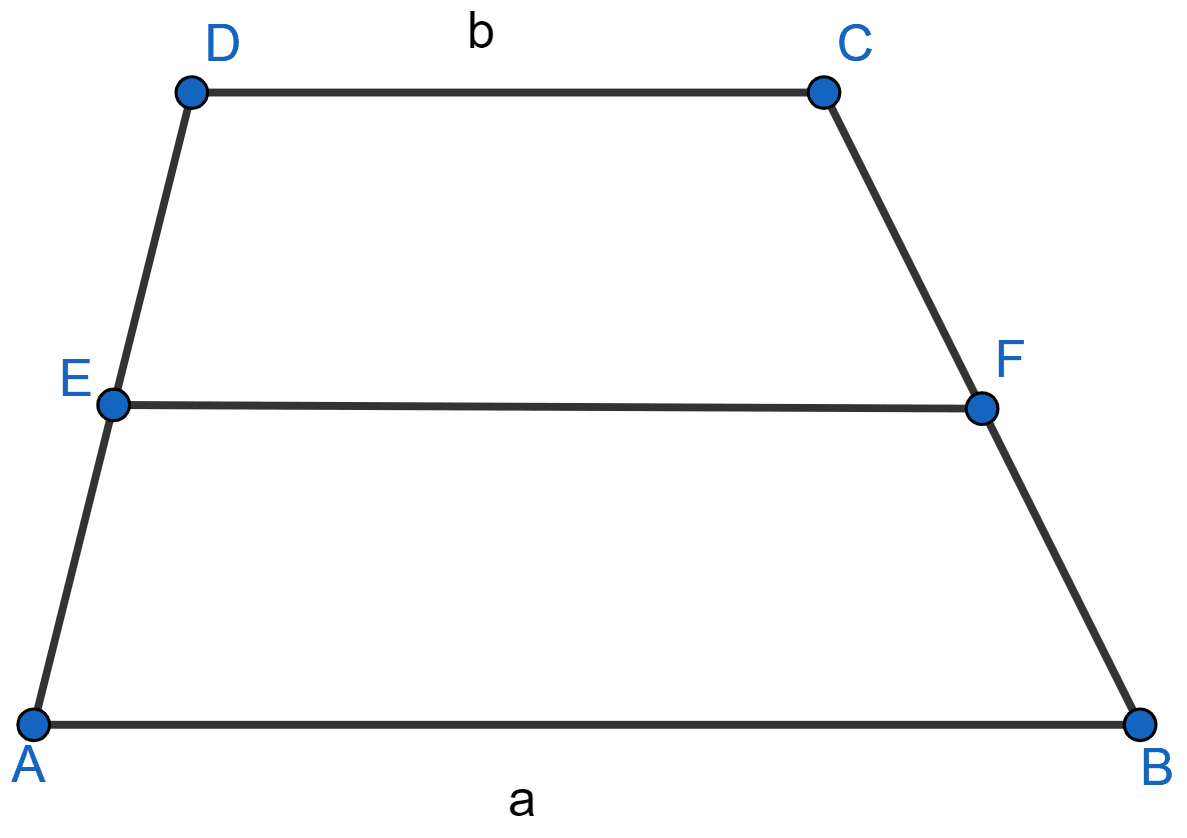
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
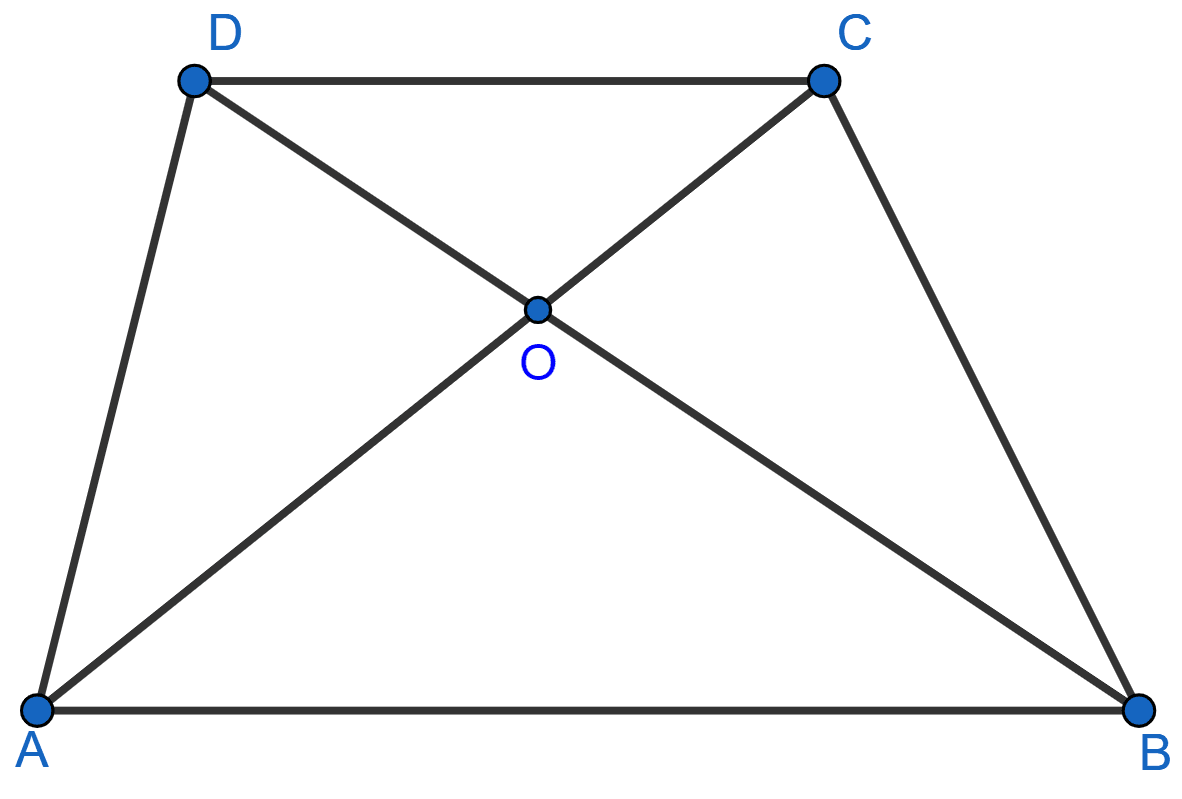
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC