Mathematics
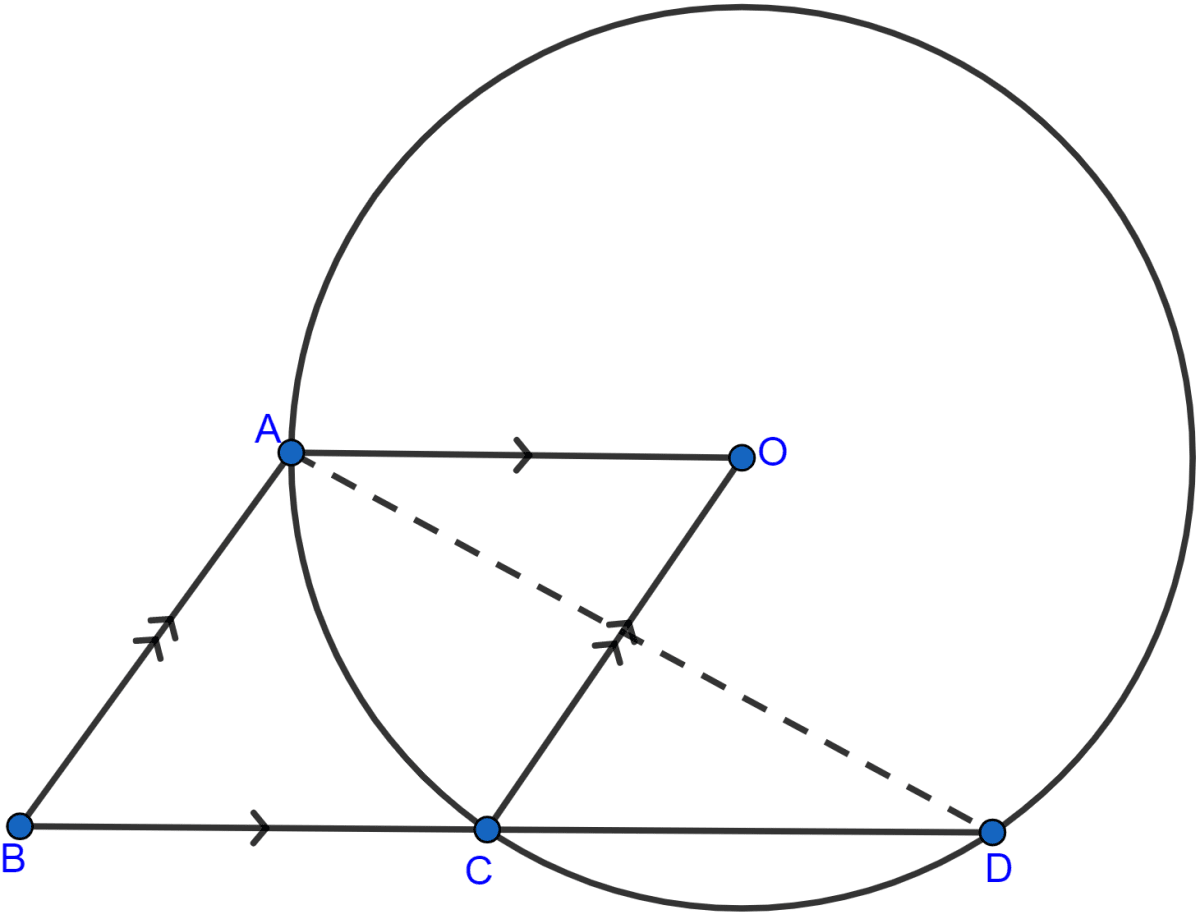
In the adjoining figure, O is the center of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2∠OAD.
Answer
Join AD.
Arc AC subtends ∠AOC at the center and ∠ADC at the point D of the circle.
∴ ∠AOC = 2∠ADC (As angle at center = double the angle at the remaining part of the circle)
∠OAD = ∠ADC (∵ alternate angles are equal.)
∴ ∠AOC = 2∠OAD …..(i)
Since, opposite angles are equal in parallelogram,
∴ ∠ABC = ∠AOC
Putting values of ∠AOC in eqn (i) we get,
∠ABC = 2∠OAD.
Hence, proved that ∠ABC = 2∠OAD.
Related Questions
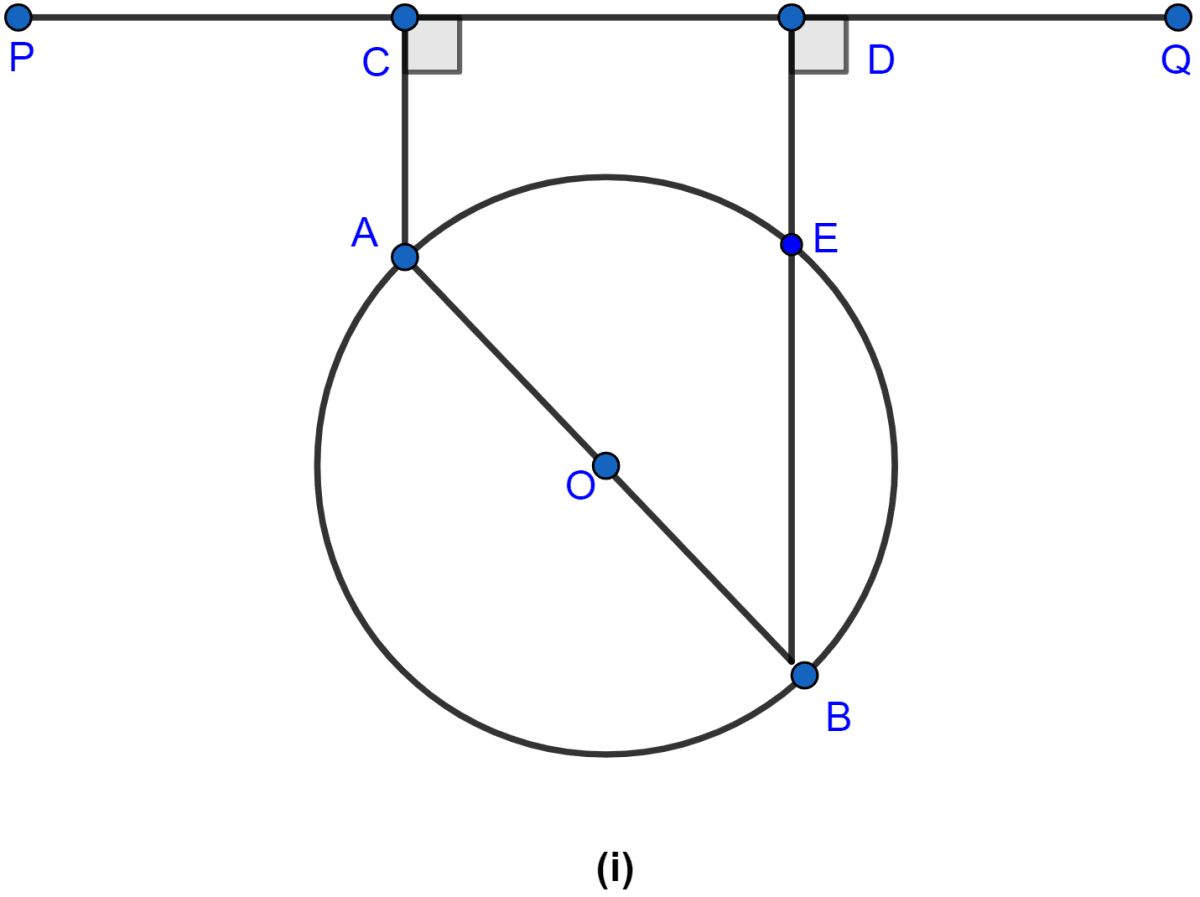
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
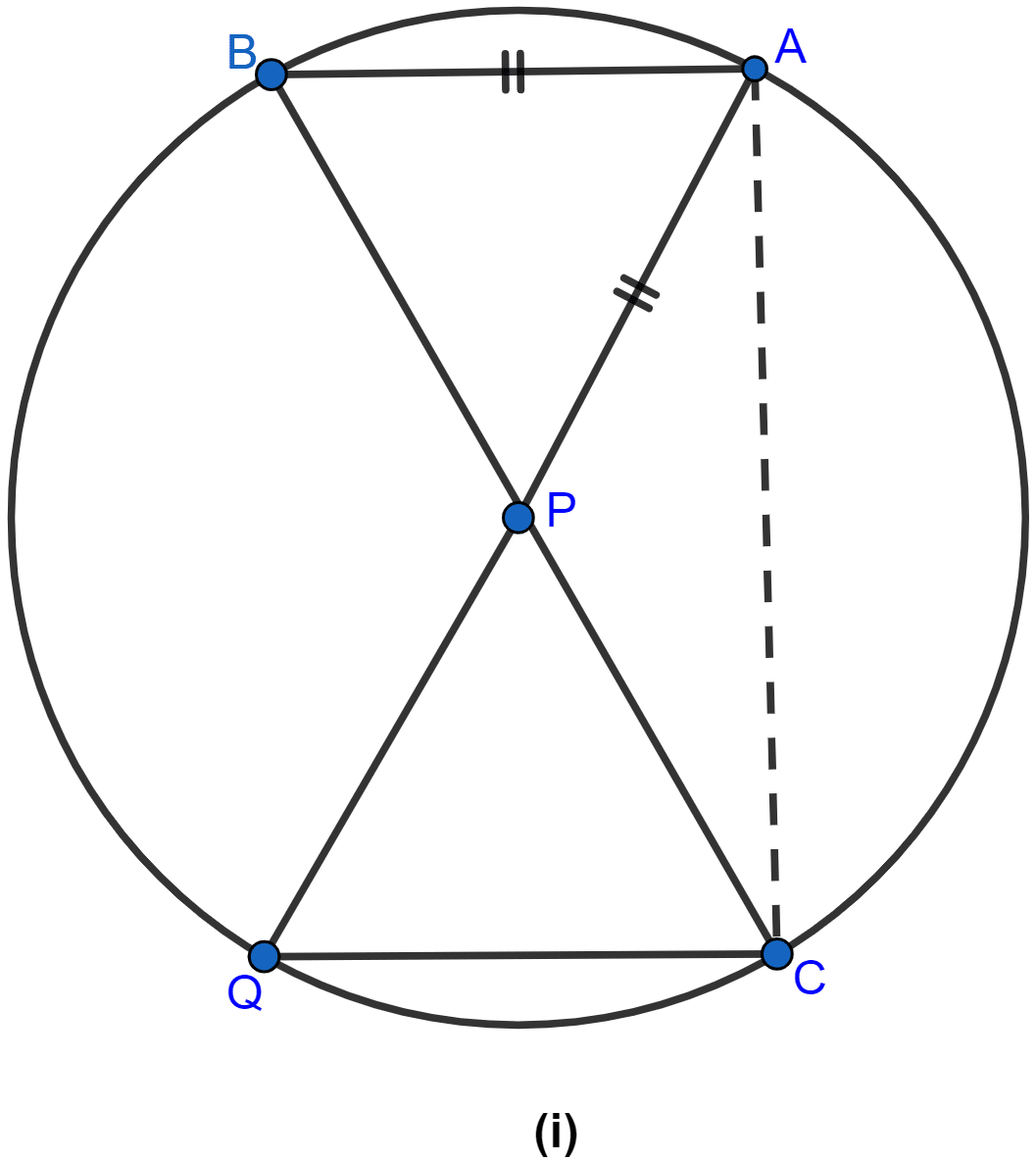
In figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.
In the figure (ii) given below, AB = AC = CD, ∠ADC = 38°. Calculate
(i) ∠ABC
(ii) ∠BEC.
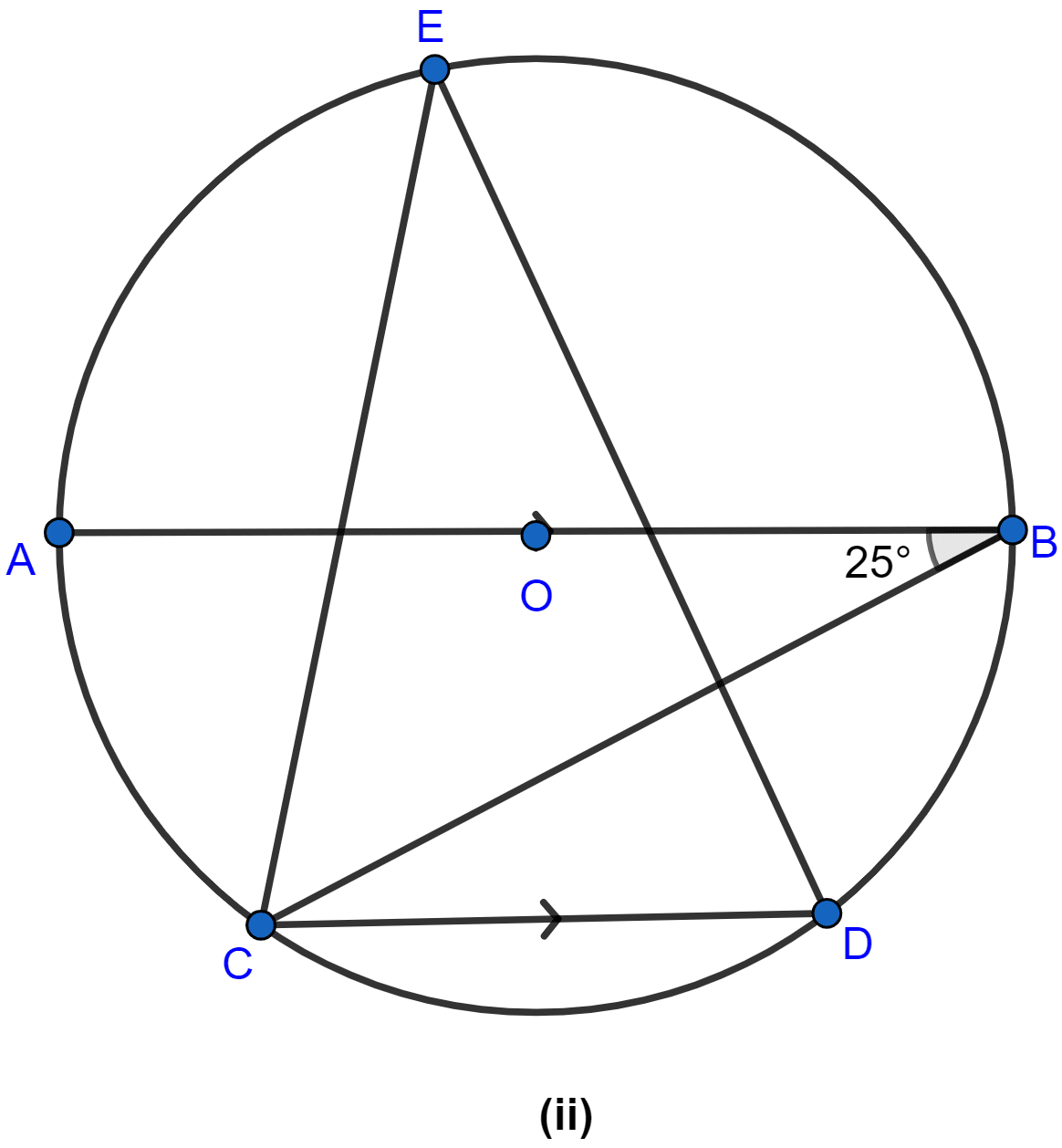
In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.