Mathematics
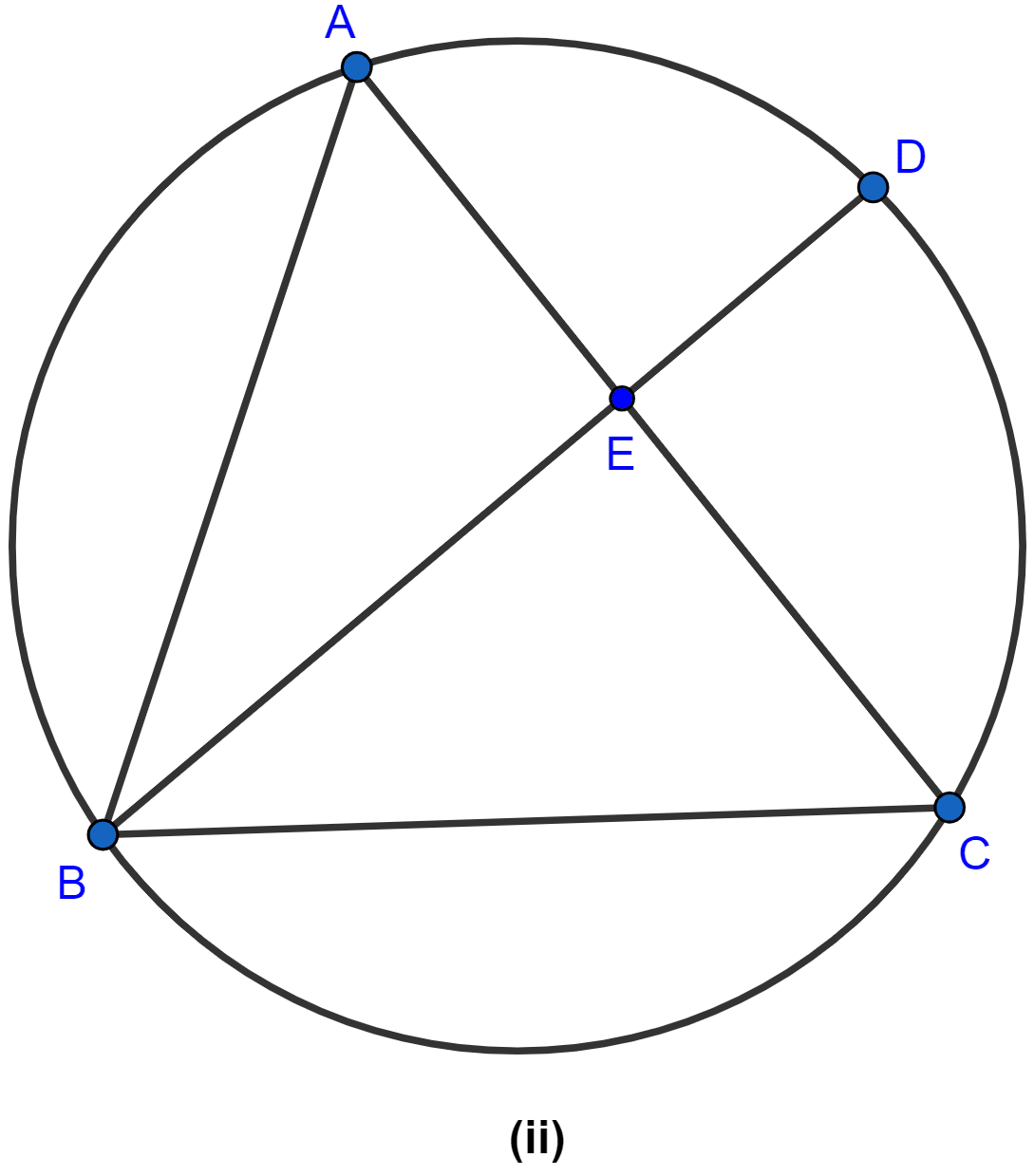
In the figure (ii) given below, AB = AC = CD, ∠ADC = 38°. Calculate
(i) ∠ABC
(ii) ∠BEC.
Circles
82 Likes
Answer
(i) In △ACD,
AC = CD
∴ ∠CAD = ∠ADC = 38° (∵ angles of equal sides in triangle are equal)
∠ACB = ∠CAD + ∠ADC = 38° + 38° = 76° (∵ exterior angle = sum of two opposite interior angles.)
In △ABC,
AB = AC
∴ ∠ABC = ∠ACB = 76° (As angles of equal sides in triangle are equal)
Hence, the value of ∠ABC = 76°.
(ii) We know that sum of angles in a triangle = 180°.
⇒ ∠BAC + ∠ABC + ∠ACB = 180°
⇒ ∠BAC + 76° + 76° = 180°
⇒ ∠BAC + 152° = 180°
⇒ ∠BAC = 180° - 152°
⇒ ∠BAC = 28°.
∠BEC = ∠BAC (∵ angles in same segment are equal.)
∠BEC = 28°.
Hence, the value of ∠BEC = 28°.
Answered By
55 Likes
Related Questions
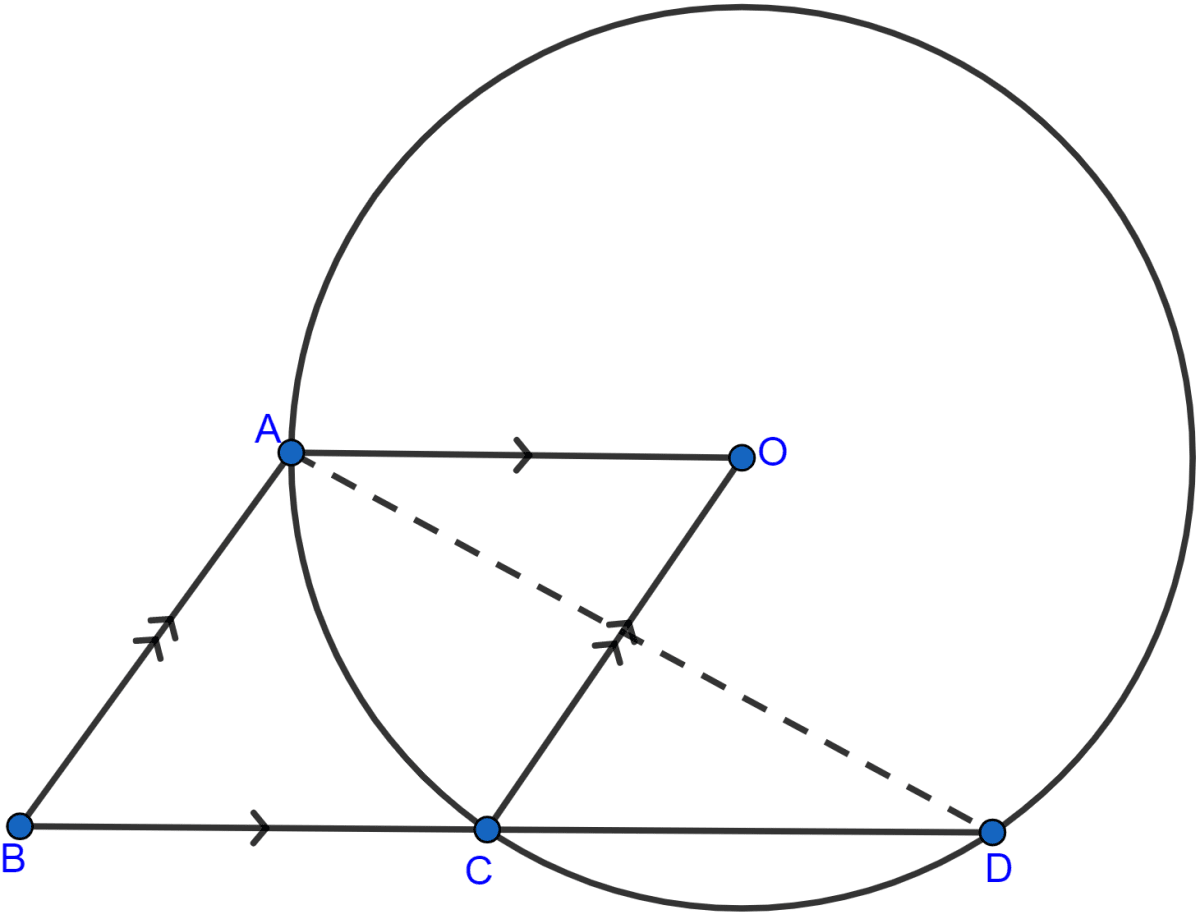
In the adjoining figure, O is the center of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2∠OAD.
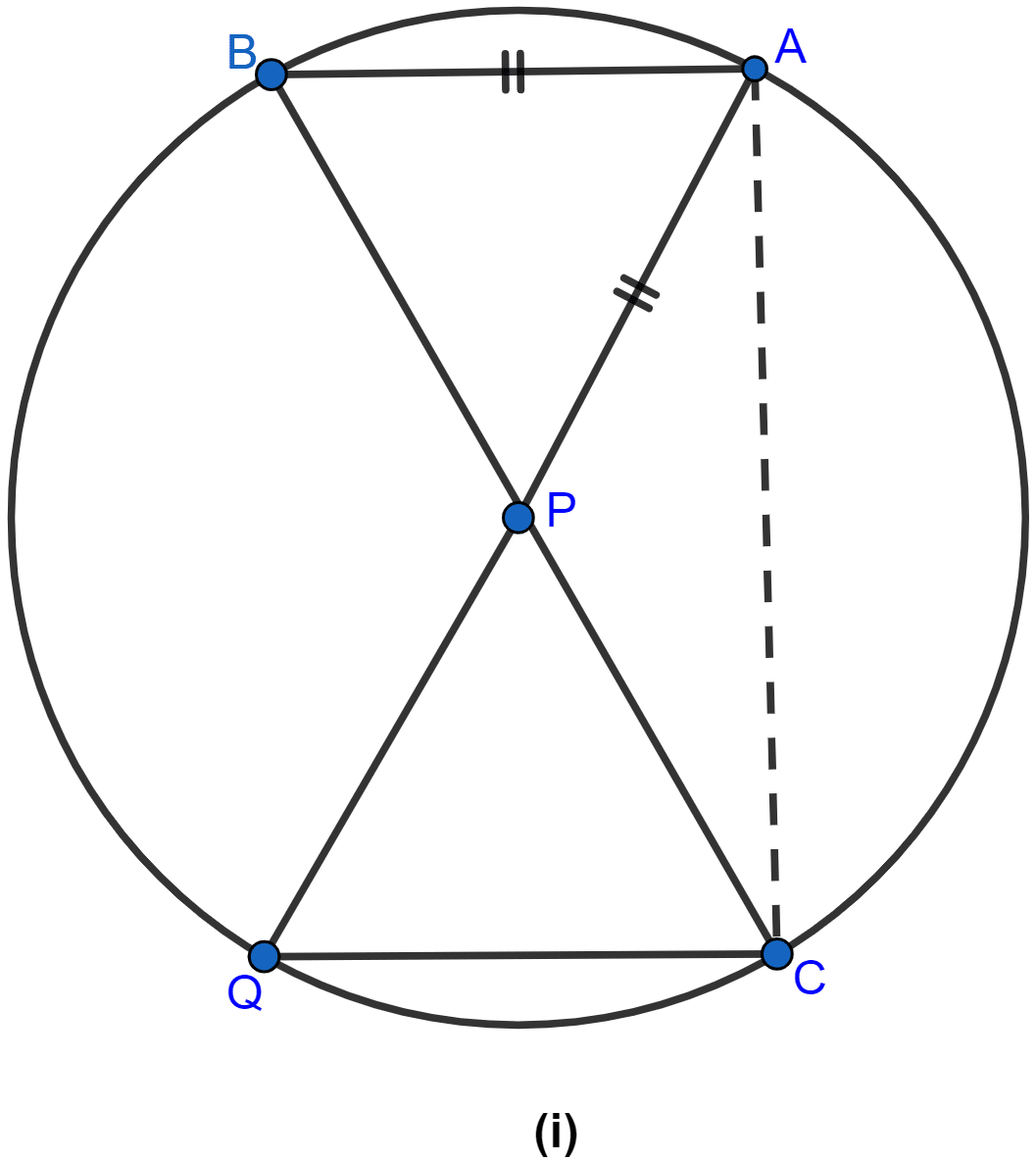
In figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.
In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.

In the figure (ii) given below, BD bisects ∠ABC. Prove that .