Mathematics
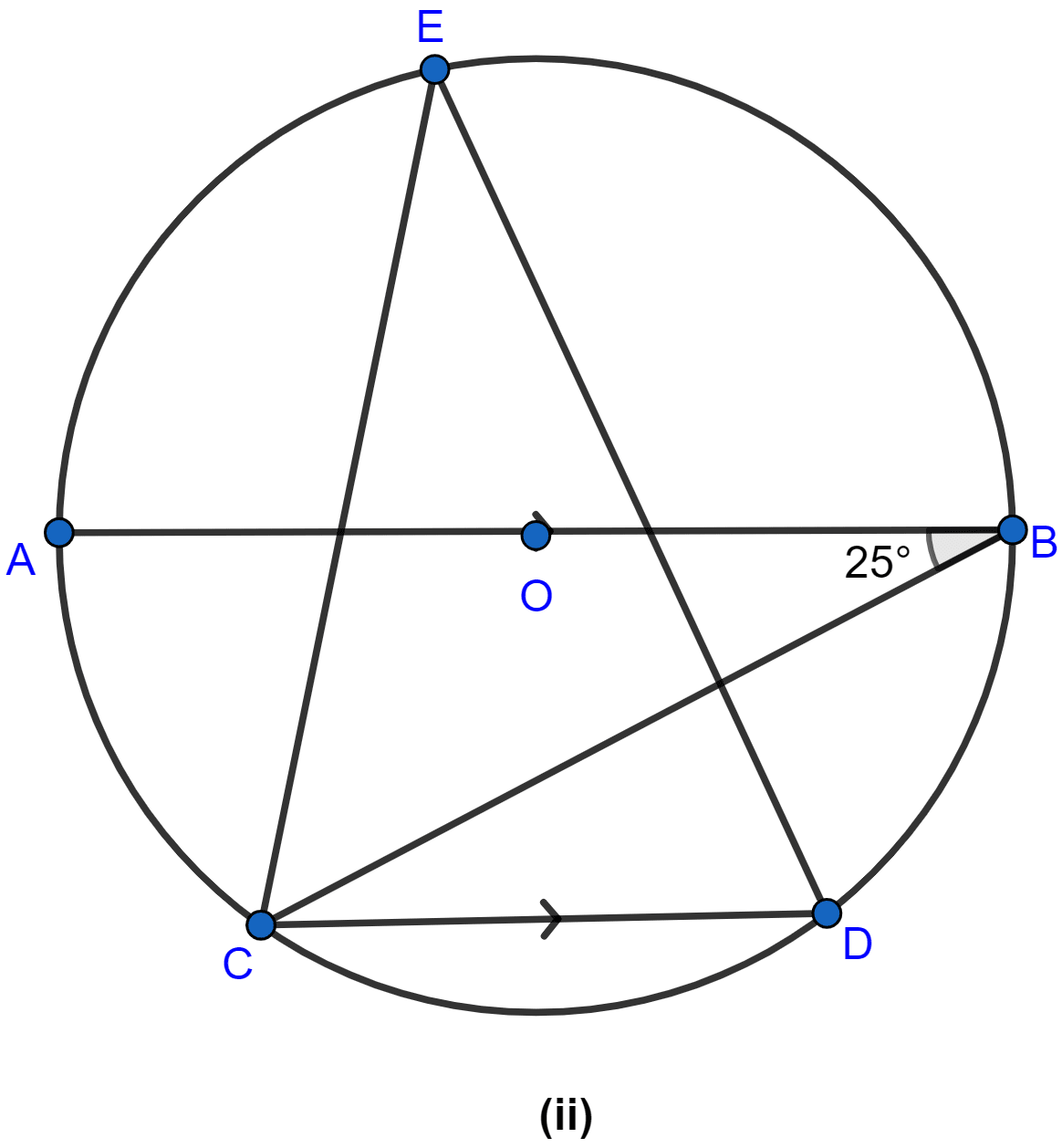
In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.
Circles
59 Likes
Answer
Join OC and OD as shown in the figure below:
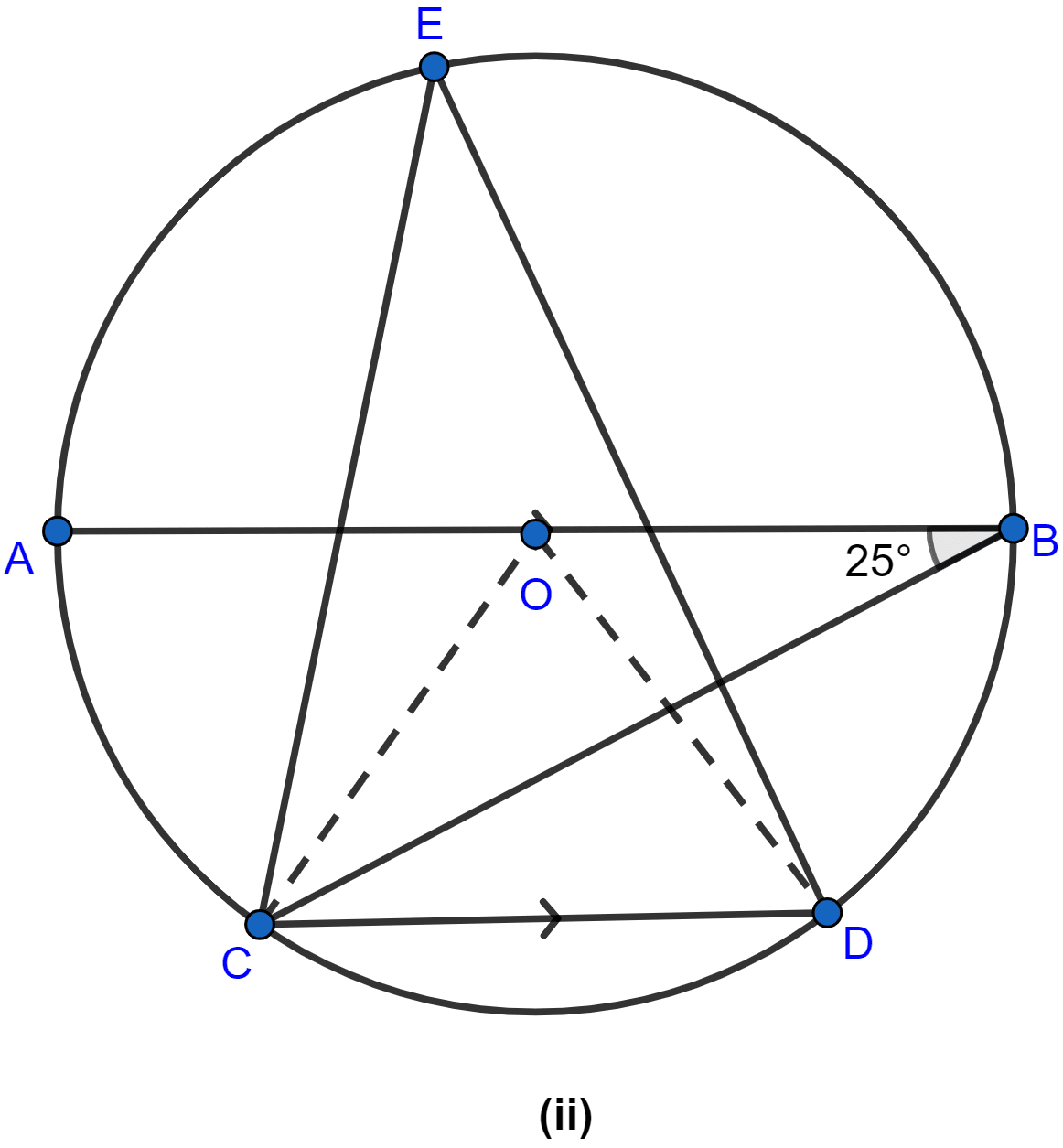
AC subtends angle AOC at centre and ∠ABC at point B.
∴ ∠AOC = 2∠ABC = 2 × 25° = 50°.
From figure,
∠OCD = ∠AOC (Alternate angles)
Hence, ∠OCD = 50°.
In △OCD,
OC = OD (Both are radius of the circle)
so, ∠ODC = ∠OCD.
Since, sum of angles of a triangle is 180°.
⇒ ∠COD + ∠OCD + ∠ODC = 180°
⇒ ∠COD + 50° + 50° = 180°
⇒ ∠COD + 100° = 180°
⇒ ∠COD = 80°.
CD subtends ∠COD at center and ∠CED at point E of the circle.
∴ ∠COD = 2∠CED
⇒ 80° = 2∠CED
⇒ ∠CED = 40°.
Hence, ∠CED = 40°.
Answered By
35 Likes
Related Questions
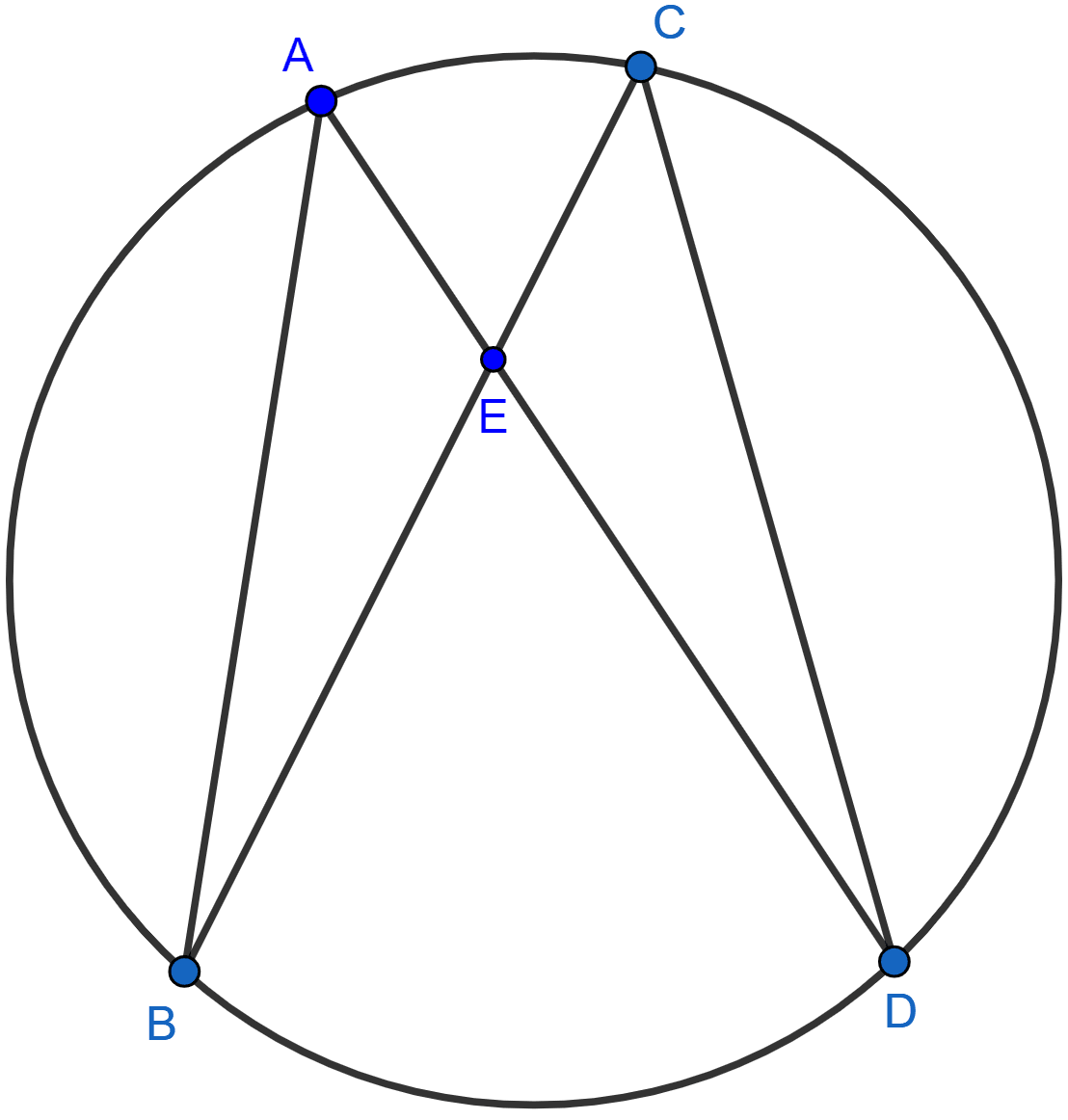
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
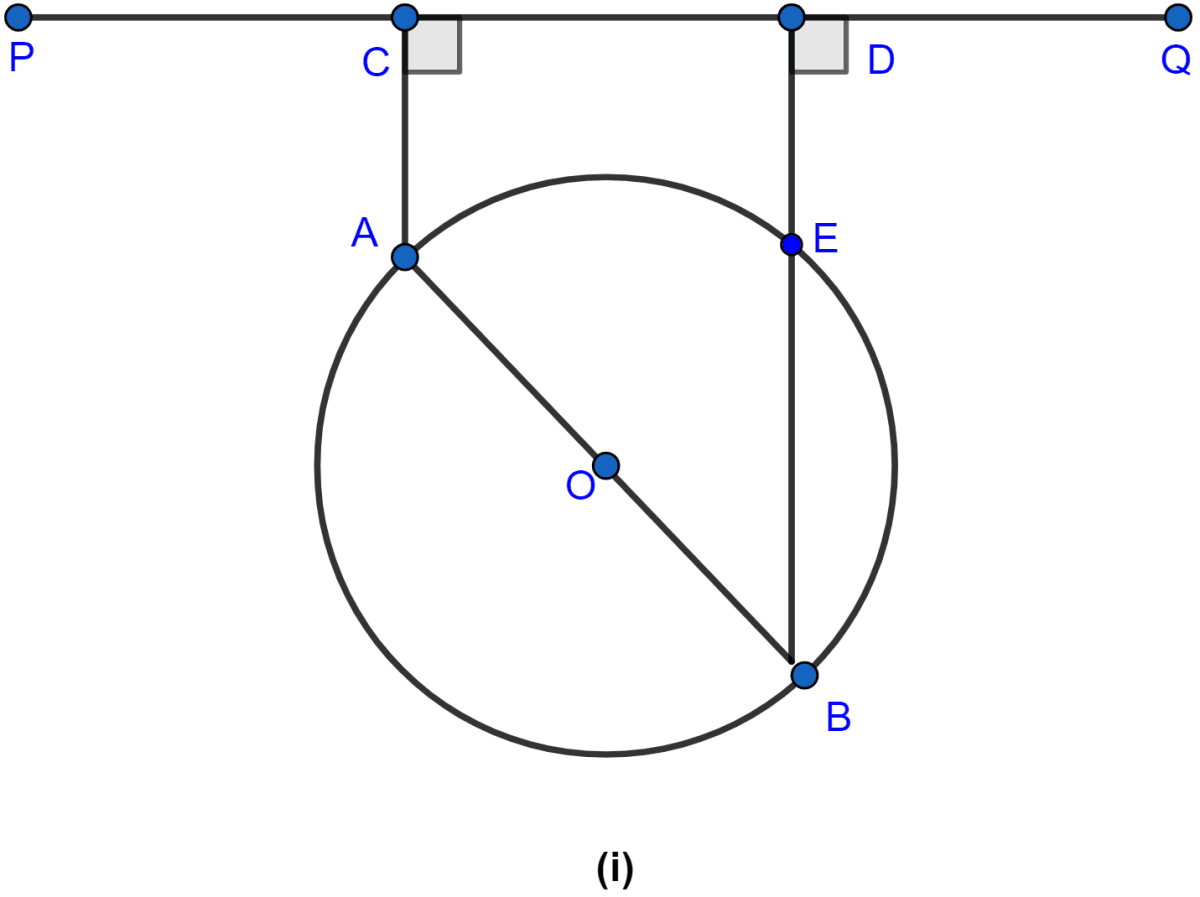
In the adjoining figure, O is the center of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2∠OAD.
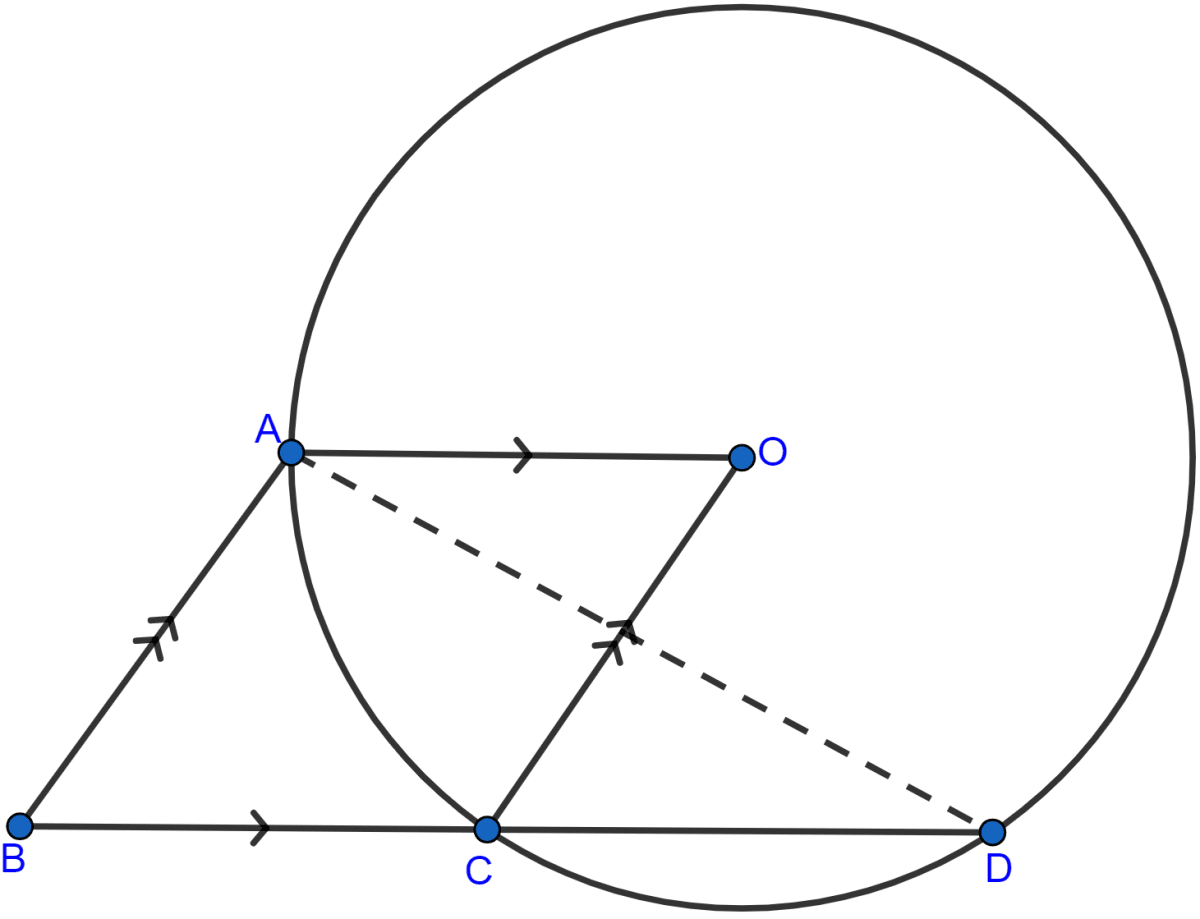
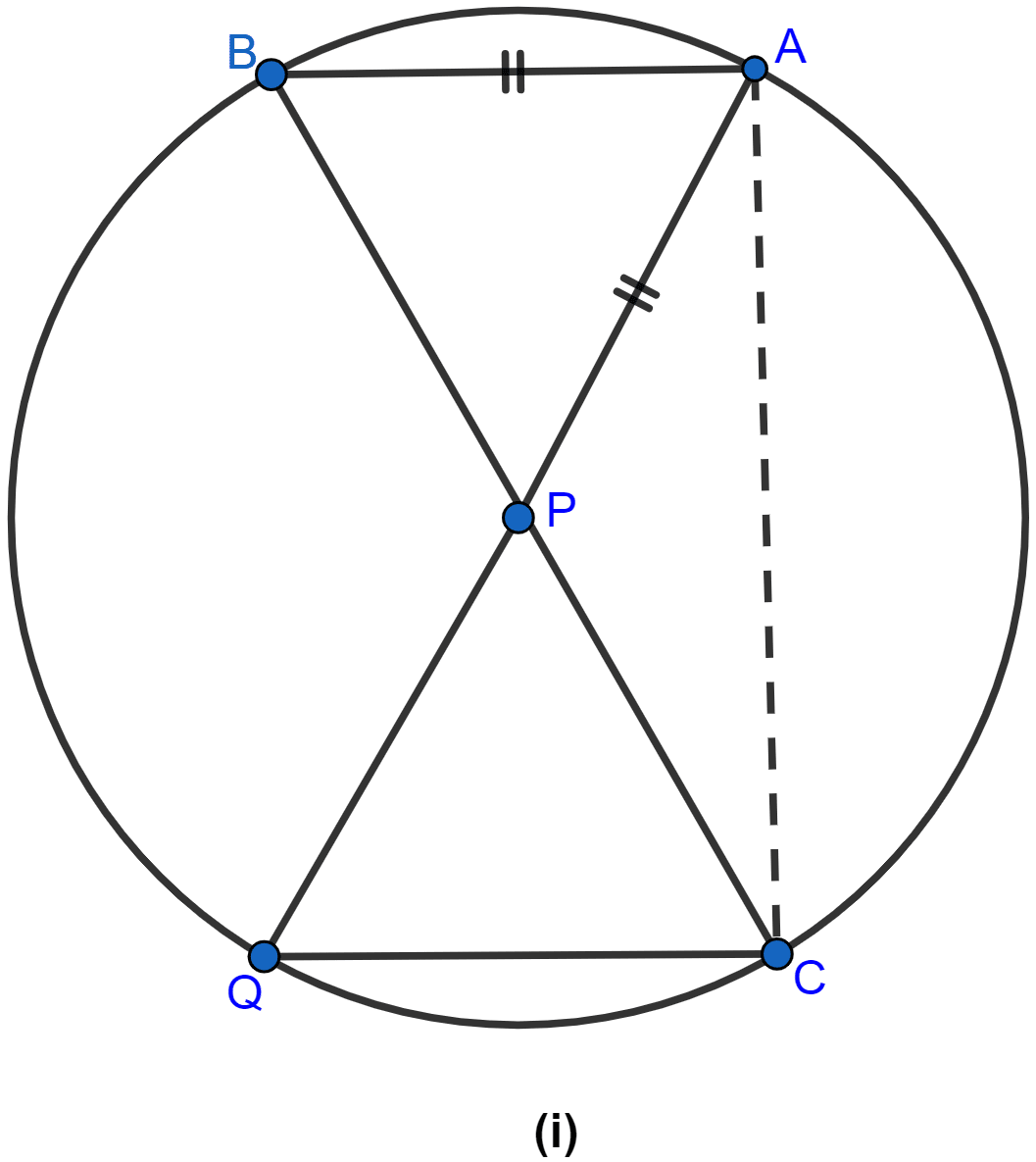
In figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.