Mathematics
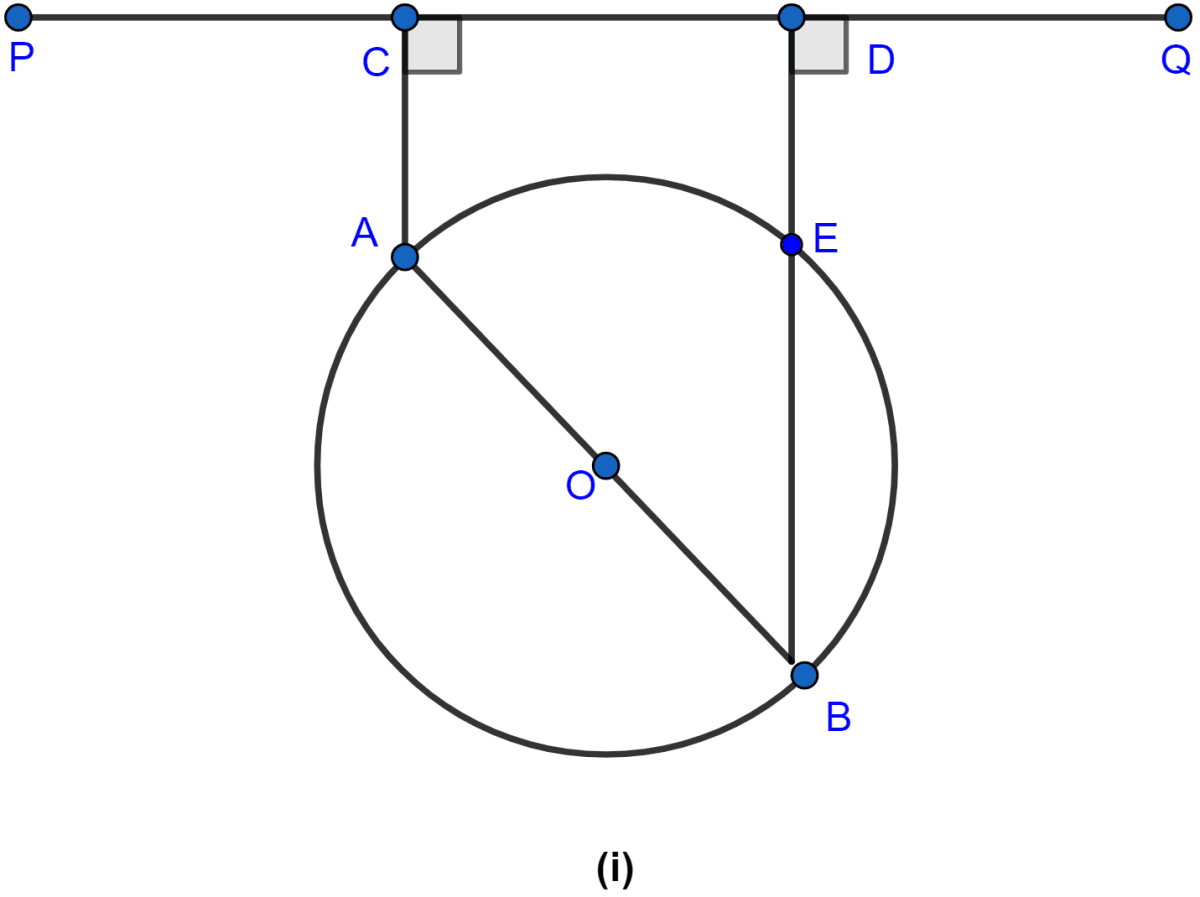
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
Circles
69 Likes
Answer
Join AE.
∠AEB = 90° (∵ angle in semicircle is 90°.)
∠AED = 90° (∵ ∠AEB and ∠AED form a linear pair.)
Hence, we can say that,
DE is also perpendicular to AE, since DE is also perpendicular to PQ hence,
AE || PQ.
Since, CA and DE both are perpendicular to PQ hence,
CA || DE.
Hence, proved that ACDE is a rectangle.
In rectangle opposite sides are equal so,
AC = DE.
Hence, proved that AC = DE.
Answered By
33 Likes
Related Questions
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
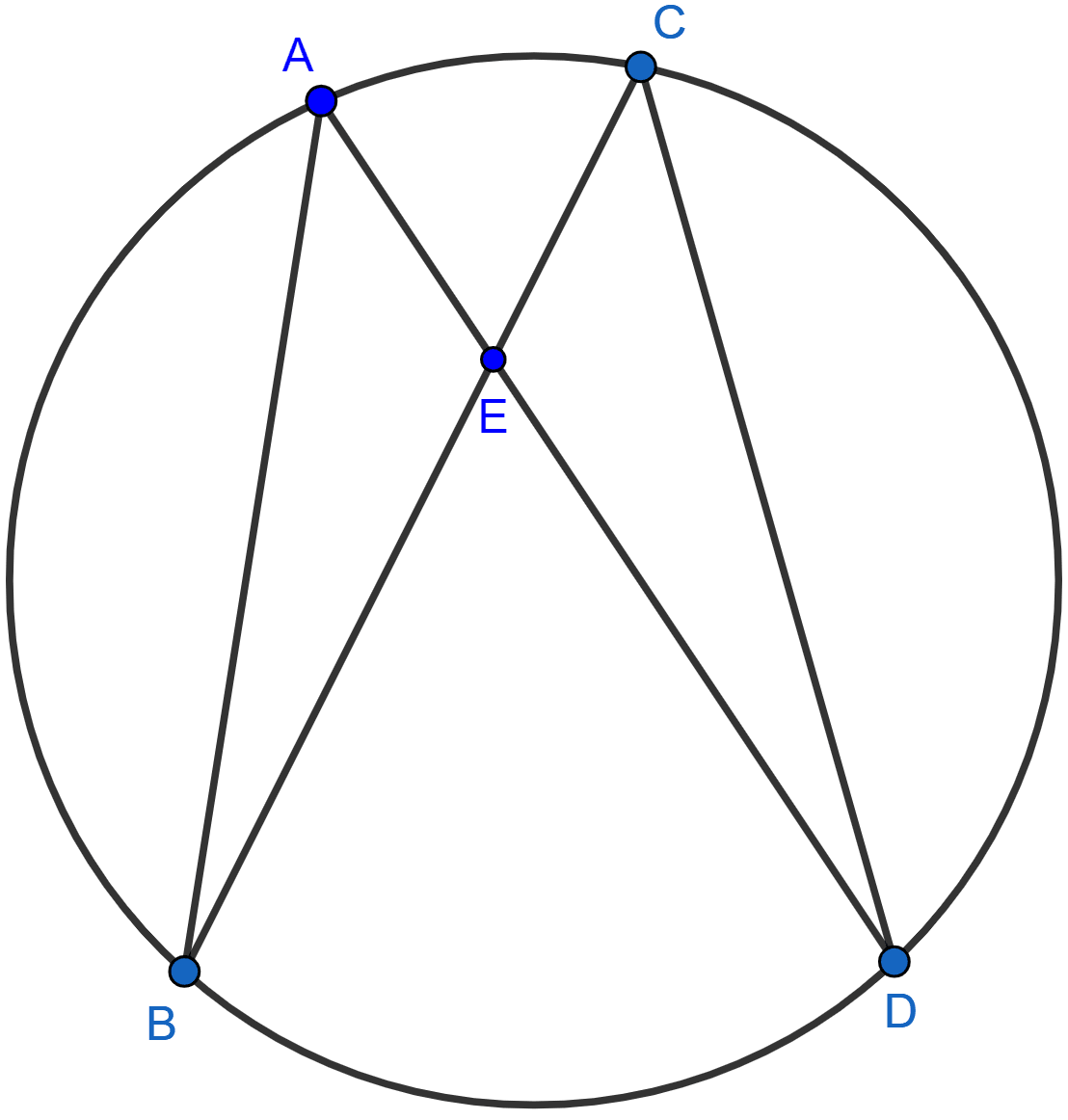
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.
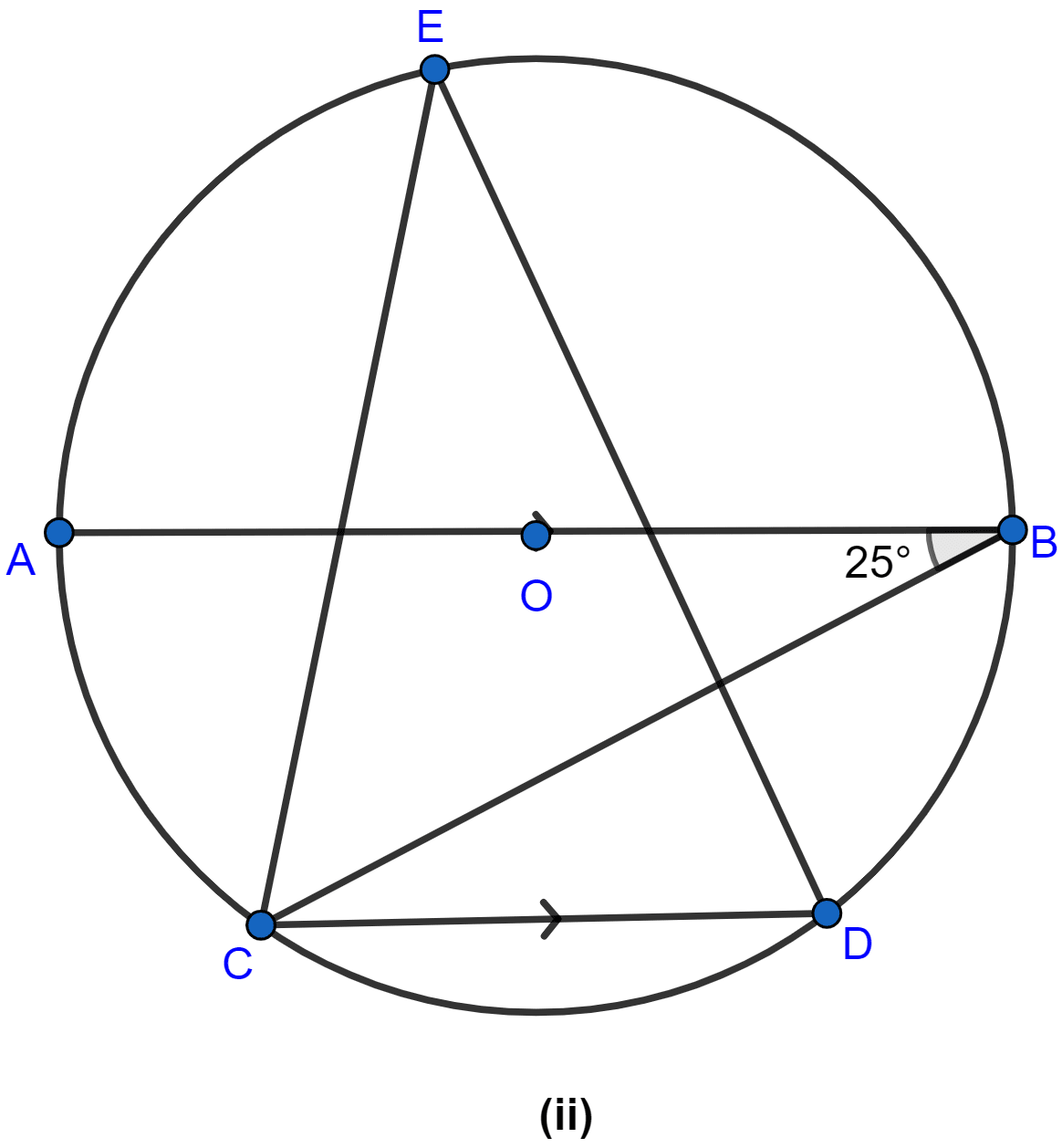
In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.
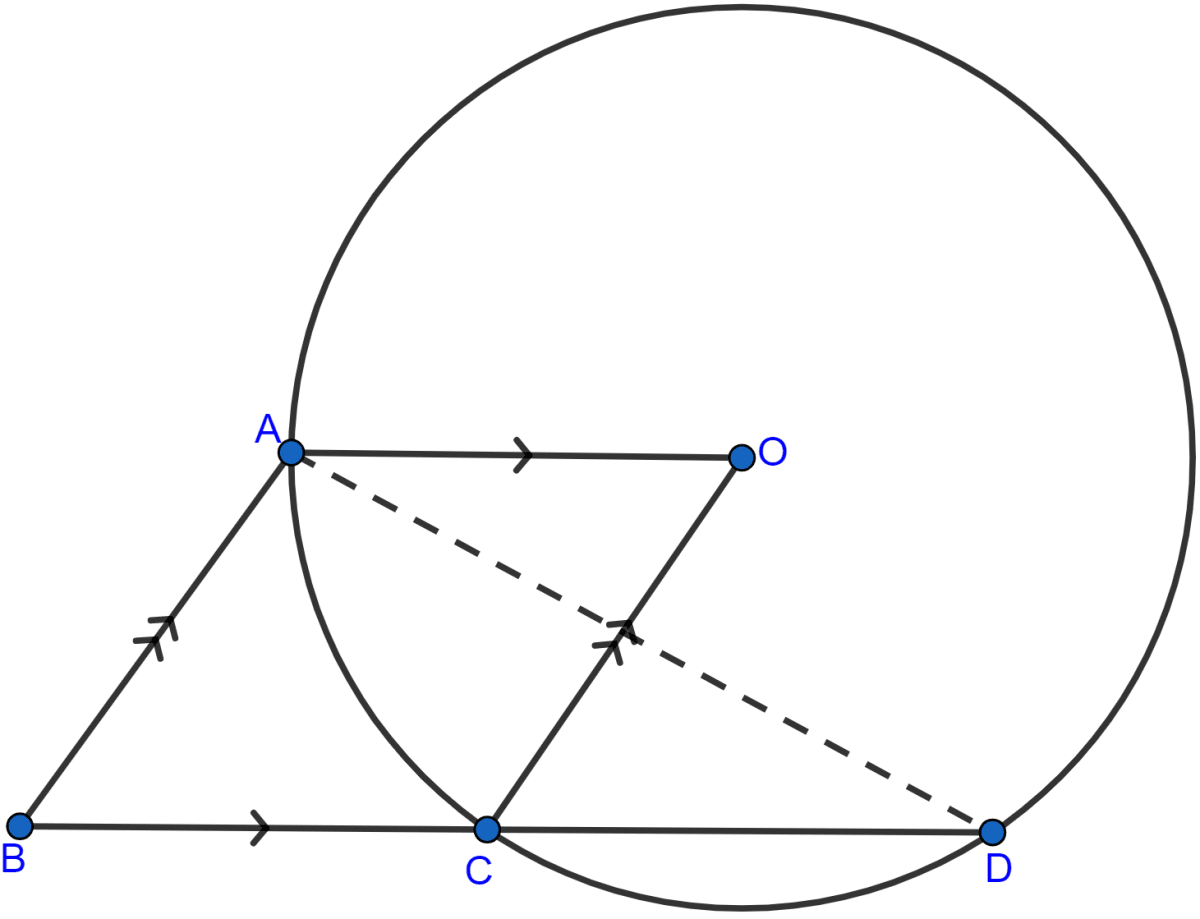
In the adjoining figure, O is the center of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2∠OAD.