Mathematics
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
Circles
27 Likes
Answer
From the below figure:

Arc BC subtends ∠BOC at center and ∠BAC at the point A on the circle.
∴ ∠BOC = 2∠A
In △OBD and △ODC,
OD = OD (Common side)
BD = CD (As D is the mid-point of BC)
OB = OC (Radius of the same circle)
∴ △OBD ≅ △ODC (SSS rule of congruency).
∴ ∠BOD = ∠COD (As corresponding part of congruent triangles are congruent.)
Since, ∠BOD = ∠COD so,
∠BOD = ∠BOC ….(i)
∠BOC = 2∠A
∠A = ∠BOC …..(ii)
From (i) and (ii) we get,
∠BOD = ∠A
Hence, proved that ∠BOD = ∠A.
Answered By
18 Likes
Related Questions
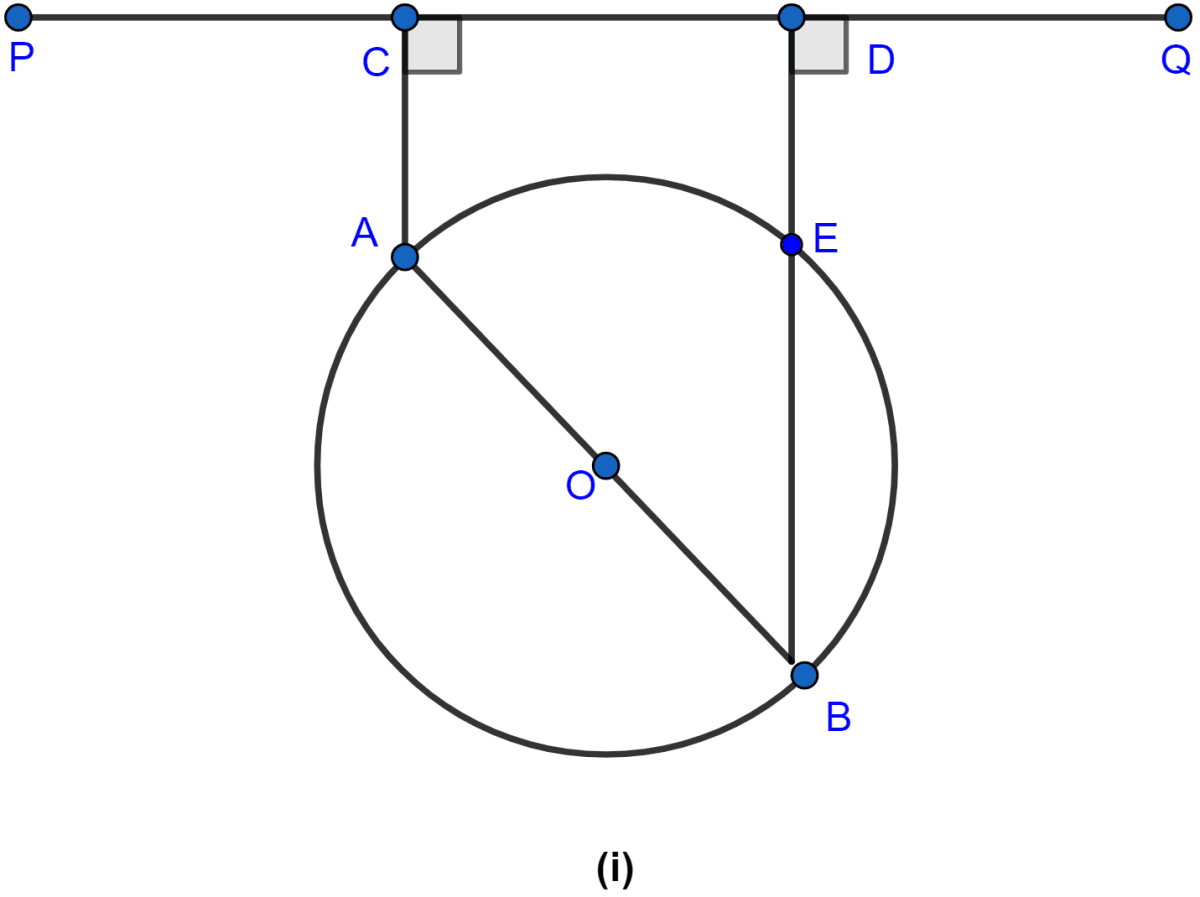
In the figure (i) given below, straight lines AB and CD pass through the center O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in
(i) ∠CDE
(ii) ∠OBE.

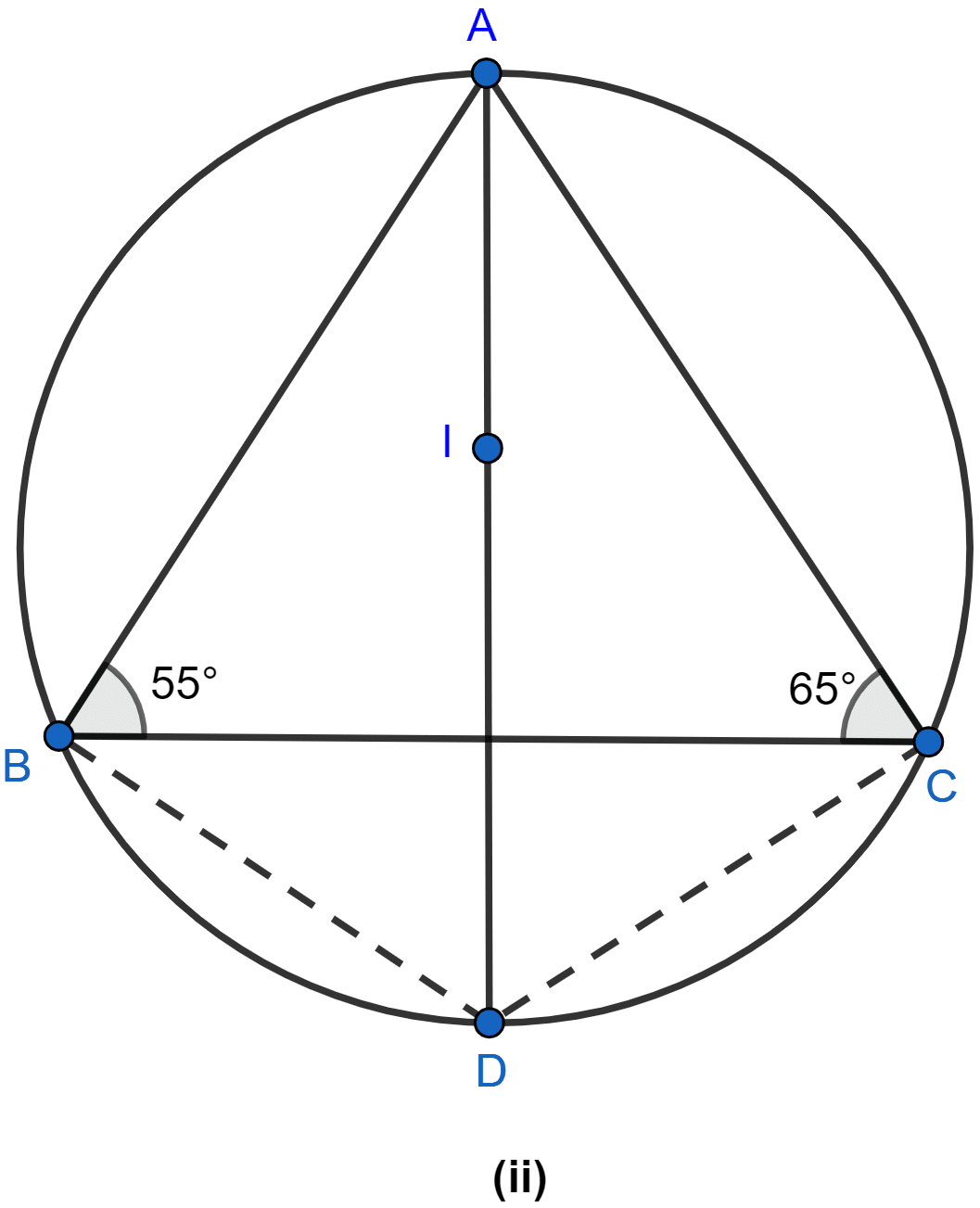
In the figure (ii) given below, I is the incentre of △ABC. AI produced meets the circumcircle of △ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
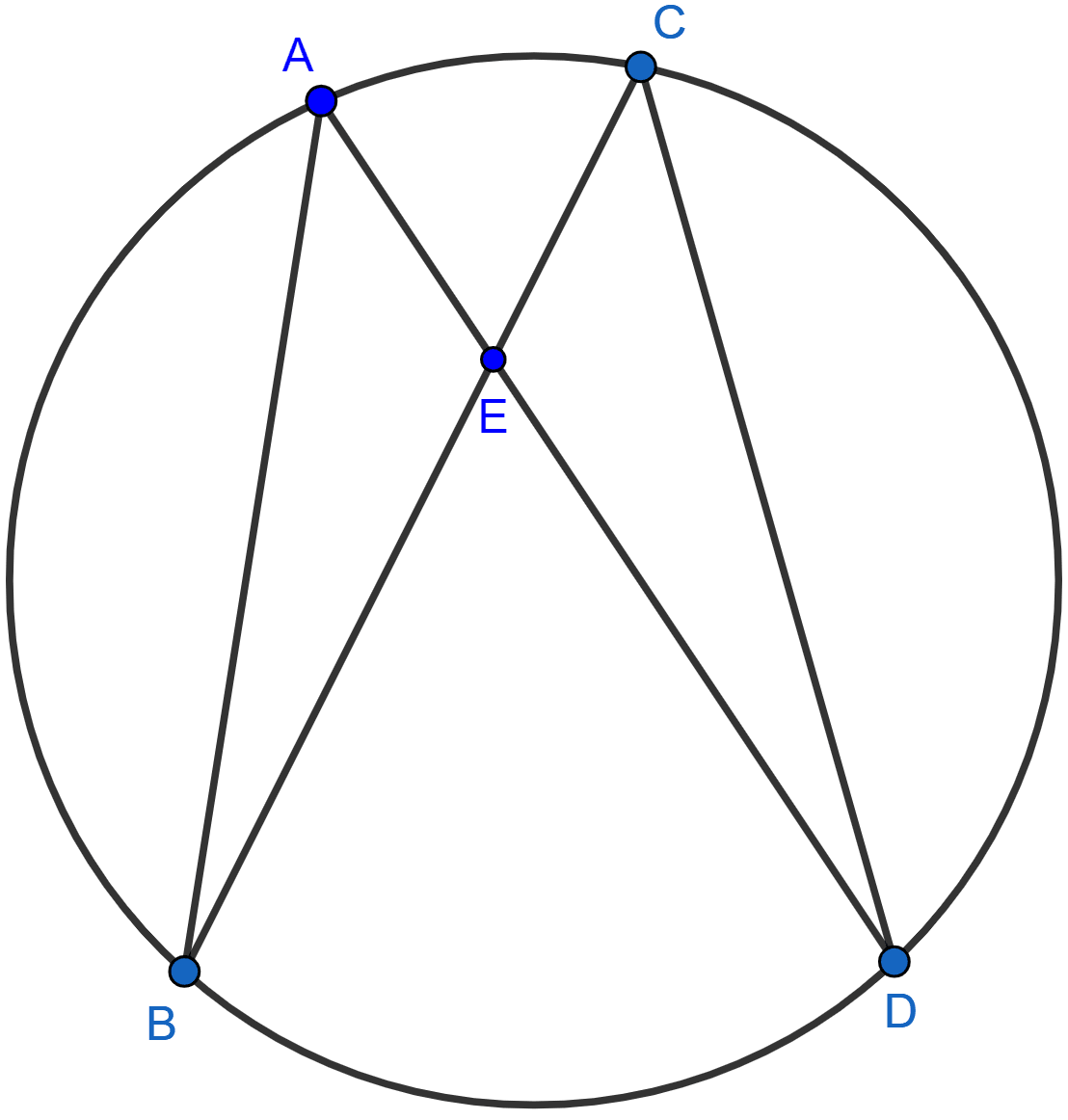
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.