Mathematics
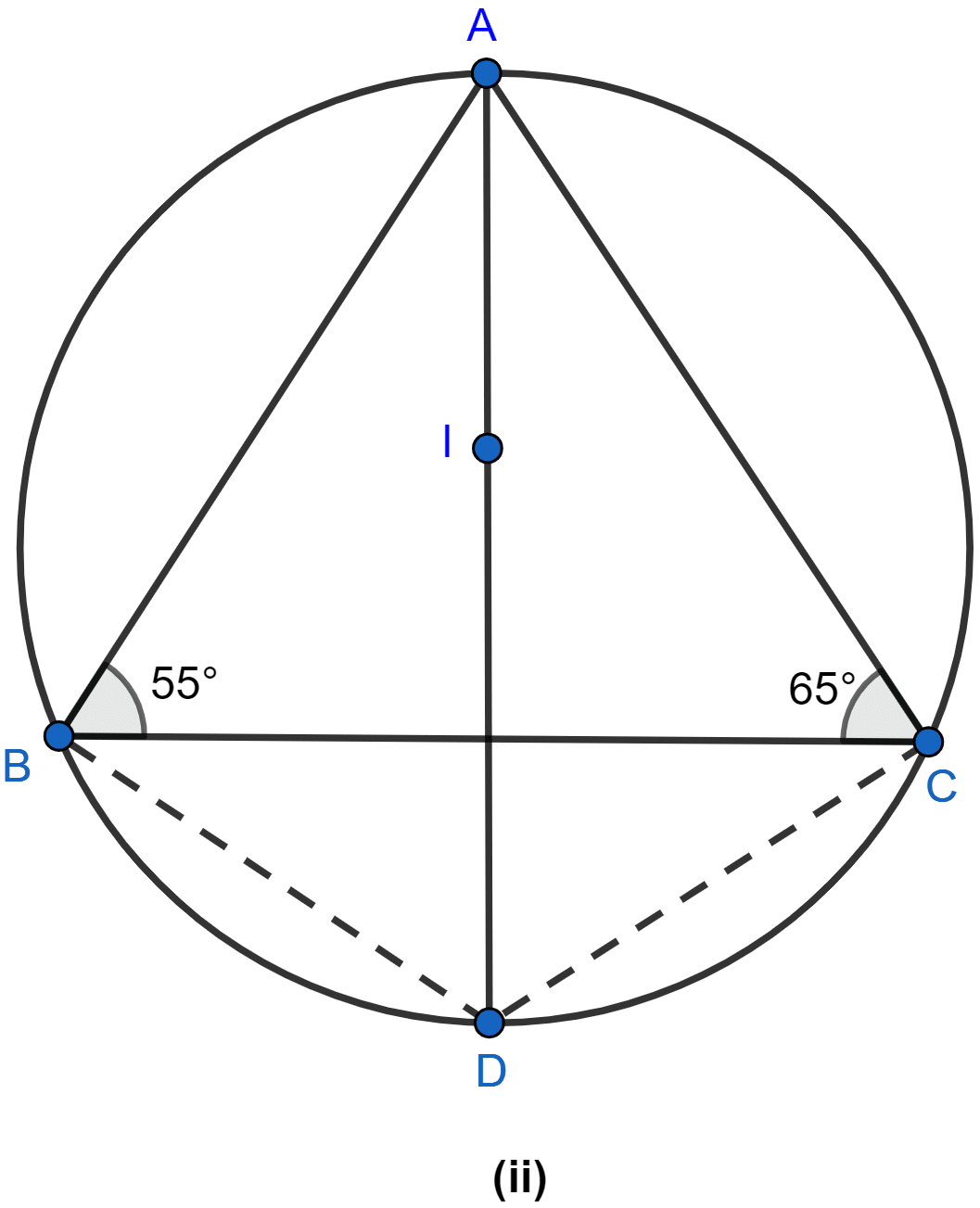
In the figure (ii) given below, I is the incentre of △ABC. AI produced meets the circumcircle of △ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
Circles
133 Likes
Answer
(i) Join BI and CI as shown in the figure below:
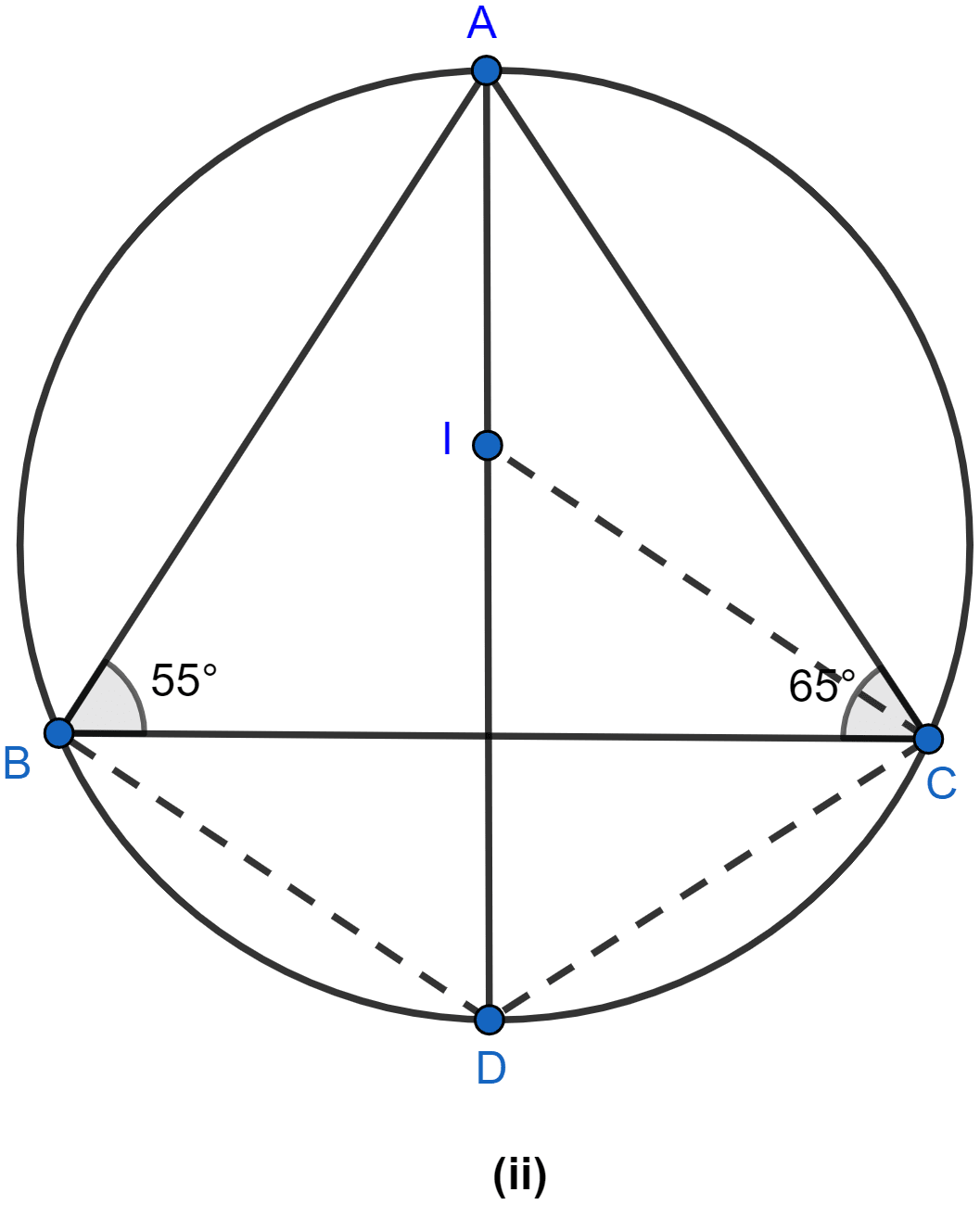
In △ABC,
⇒ ∠BAC + ∠ABC + ∠ACB = 180° (∵ sum of angles = 180°.)
⇒ ∠BAC + 55° + 65° = 180°
⇒ ∠BAC + 120° = 180°
⇒ ∠BAC = 180° - 120°
⇒ ∠BAC = 60°.
I is the incentre,
∴ I lies on the bisectors of angle of the △ABC,
∴ ∠BAD = ∠CAD = = 30°.
∠BCD = ∠BAD = 30°. (∵ angles in same segment are equal.)
Hence, the value of ∠BCD = 30°
(ii) Similarly,
∠CBD = ∠CAD = 30°. (∵ angles in same segment are equal.)
Hence, the value of ∠CBD = 30°
(iii) The line CI bisects ∠C (∵ I lies on the bisectors of angle of the △ABC).
∴ ∠BCI = .
From figure,
∠DCI = ∠BCD + ∠BCI = .
Hence, the value of ∠DCI = .
(iv) ∠IBC =
∠ICB =
∠BIC = 180° - (∠IBC + ∠ICB)
Hence, the value of ∠BIC = 120°.
Answered By
82 Likes
Related Questions
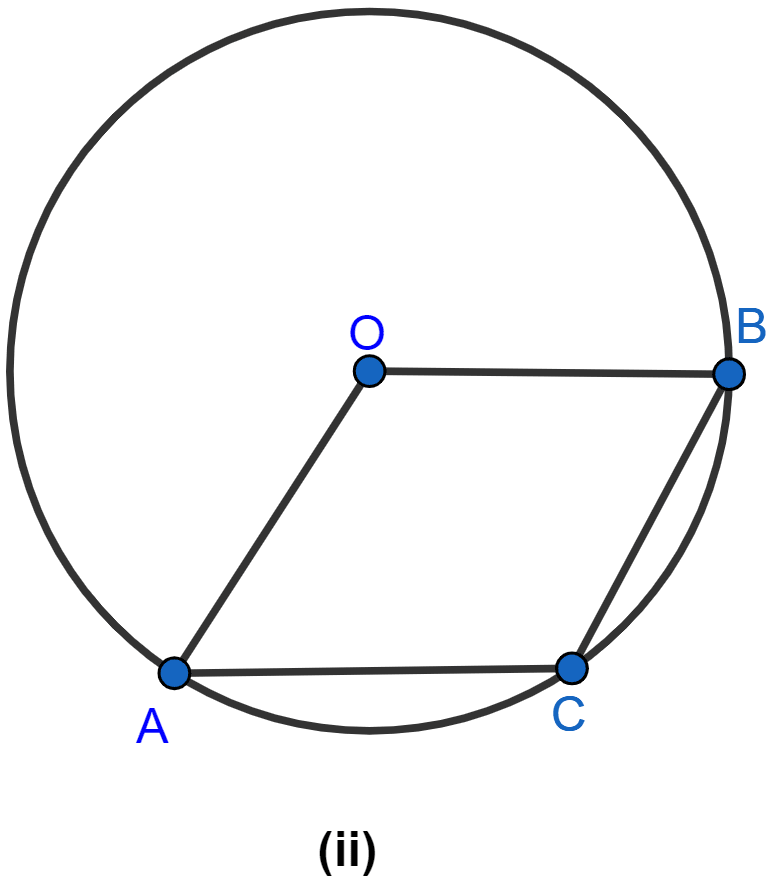
In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.
In the figure (i) given below, straight lines AB and CD pass through the center O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in
(i) ∠CDE
(ii) ∠OBE.

O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
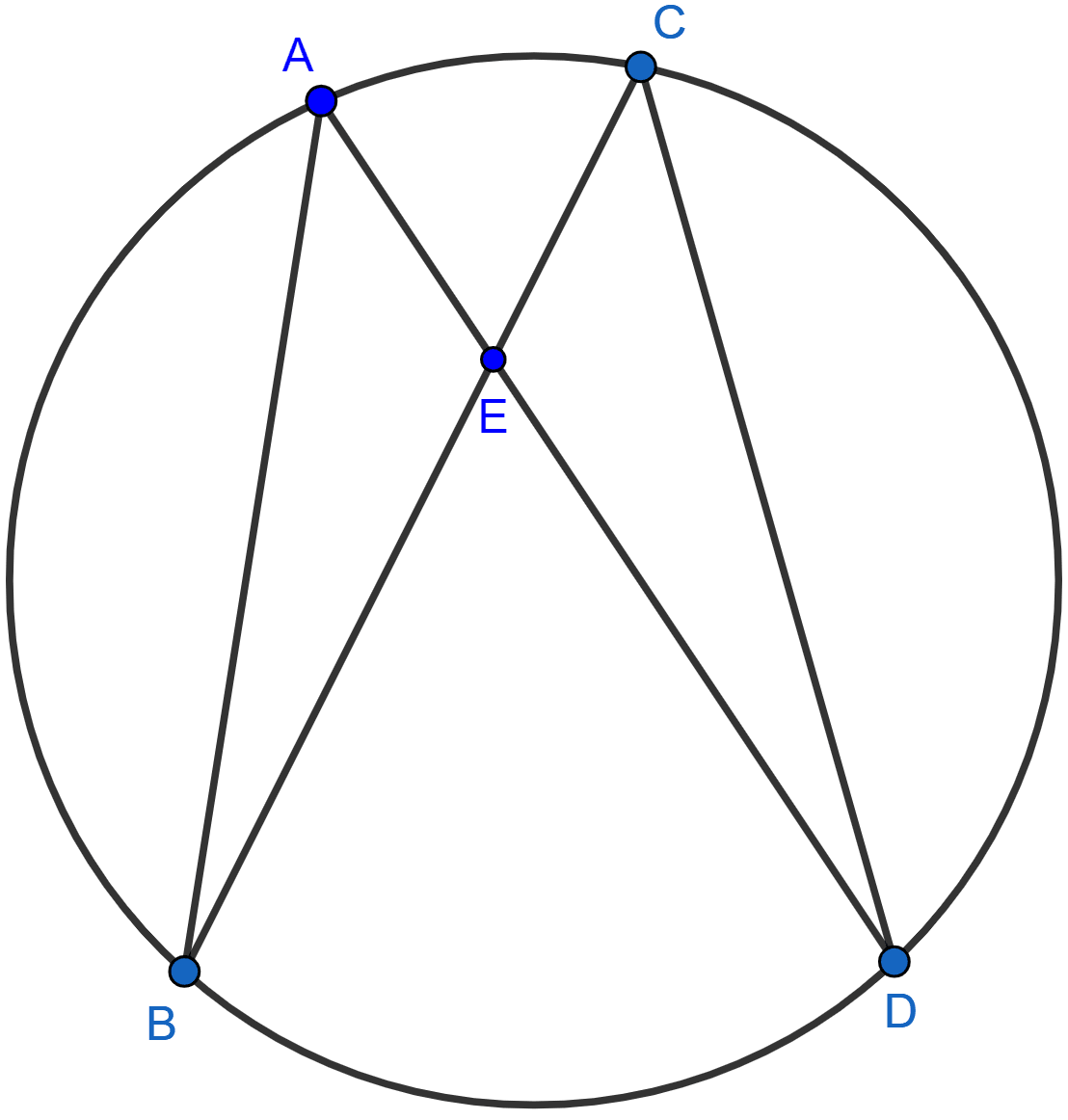
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.