Mathematics
In the figure (i) given below, straight lines AB and CD pass through the center O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in
(i) ∠CDE
(ii) ∠OBE.

Circles
77 Likes
Answer
(i) In △CED,
∠CED = 90° (∵ angle in semicircle is 90°.)
We know that sum of angles of a triangle is 180°.
⇒ ∠CED + ∠DCE + ∠CDE = 180°.
⇒ 90° + 40° + ∠CDE = 180°
⇒ ∠CDE + 130° = 180°
⇒ ∠CDE = 180° - 130°
⇒ ∠CDE = 50°.
Hence, the number of degrees in ∠CDE = 50.
(ii) From figure,
∠AOD + ∠DOB = 180° (∵ they form linear pair)
⇒ 75° + ∠DOB = 180°
⇒ ∠DOB = 180° - 75°
⇒ ∠DOB = 105°.
In △DOB,
∠ODB = ∠CDE = 50°
We know that sum of angles of a triangle is 180°.
⇒ ∠DOB + ∠ODB + ∠DBO = 180°.
⇒ 105° + 50° + ∠DBO = 180°
⇒ ∠DBO + 155° = 180°
⇒ ∠DBO = 180° - 155°
⇒ ∠DBO = 25°.
From figure,
∠OBE = ∠DBO
∴ ∠OBE = 25°.
Hence, the number of degrees in ∠OBE = 25.
Answered By
42 Likes
Related Questions
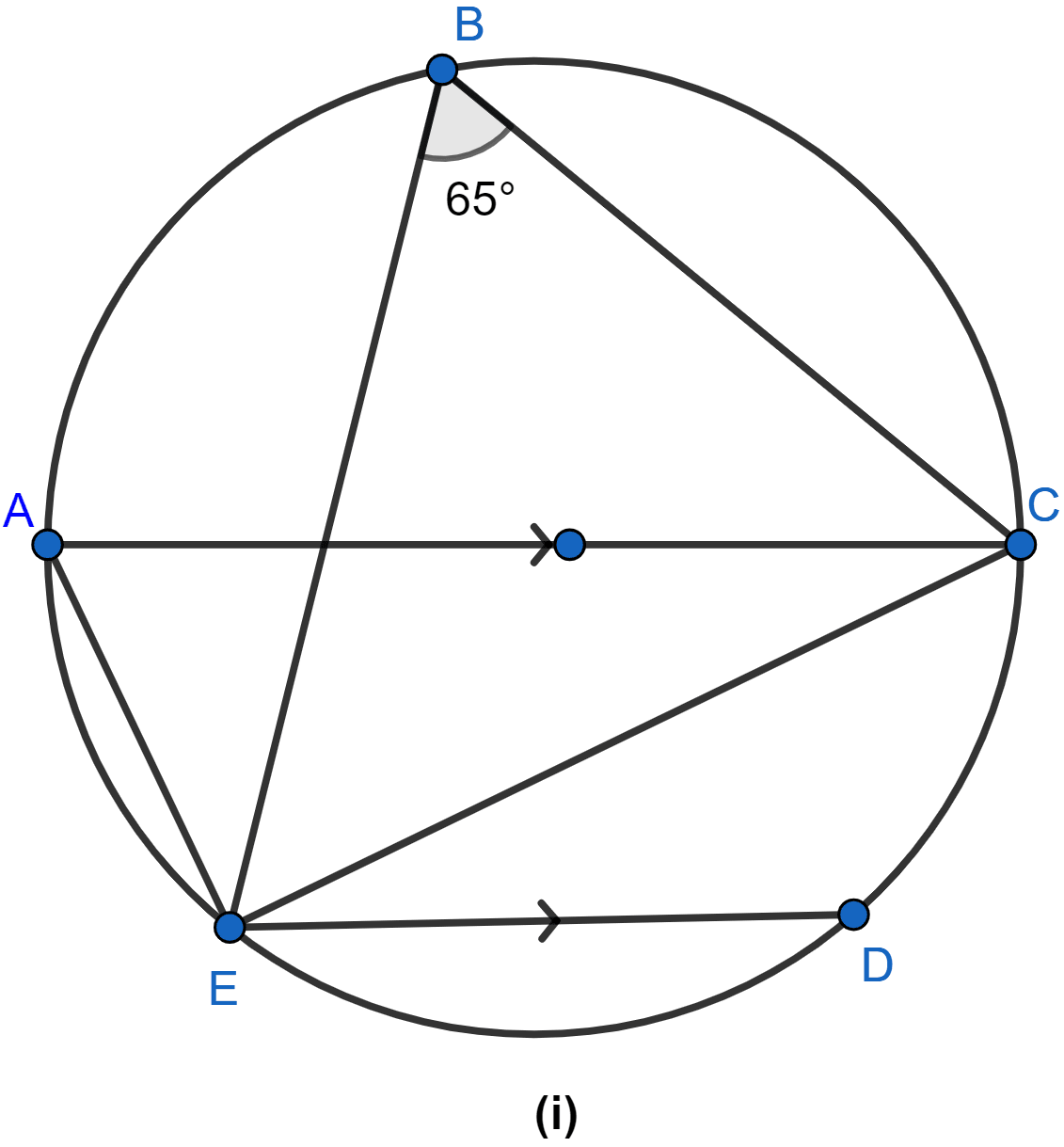
In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
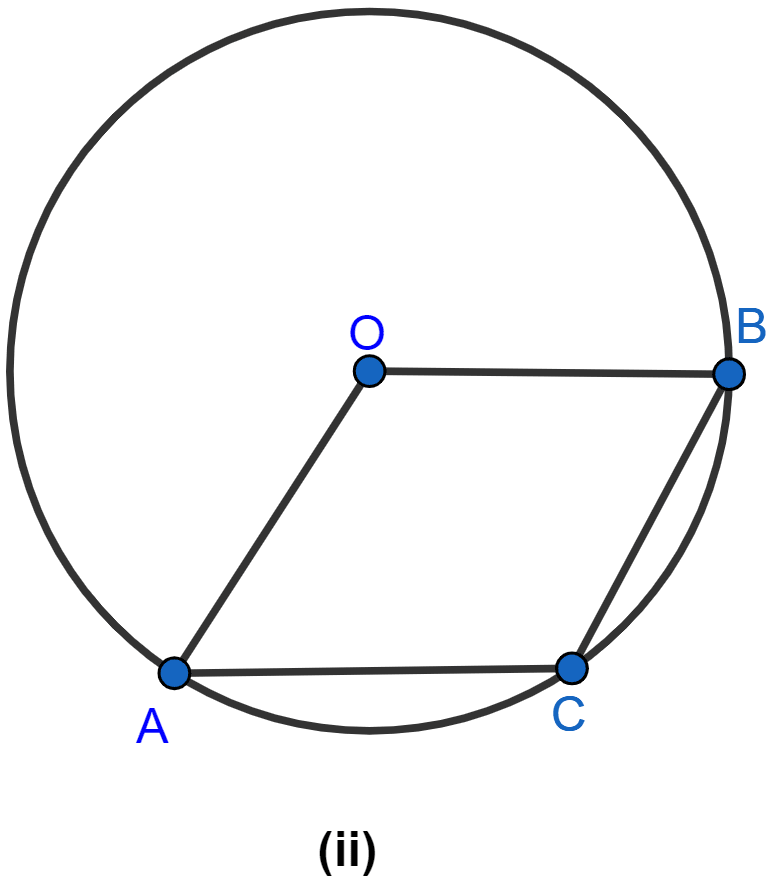
In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.
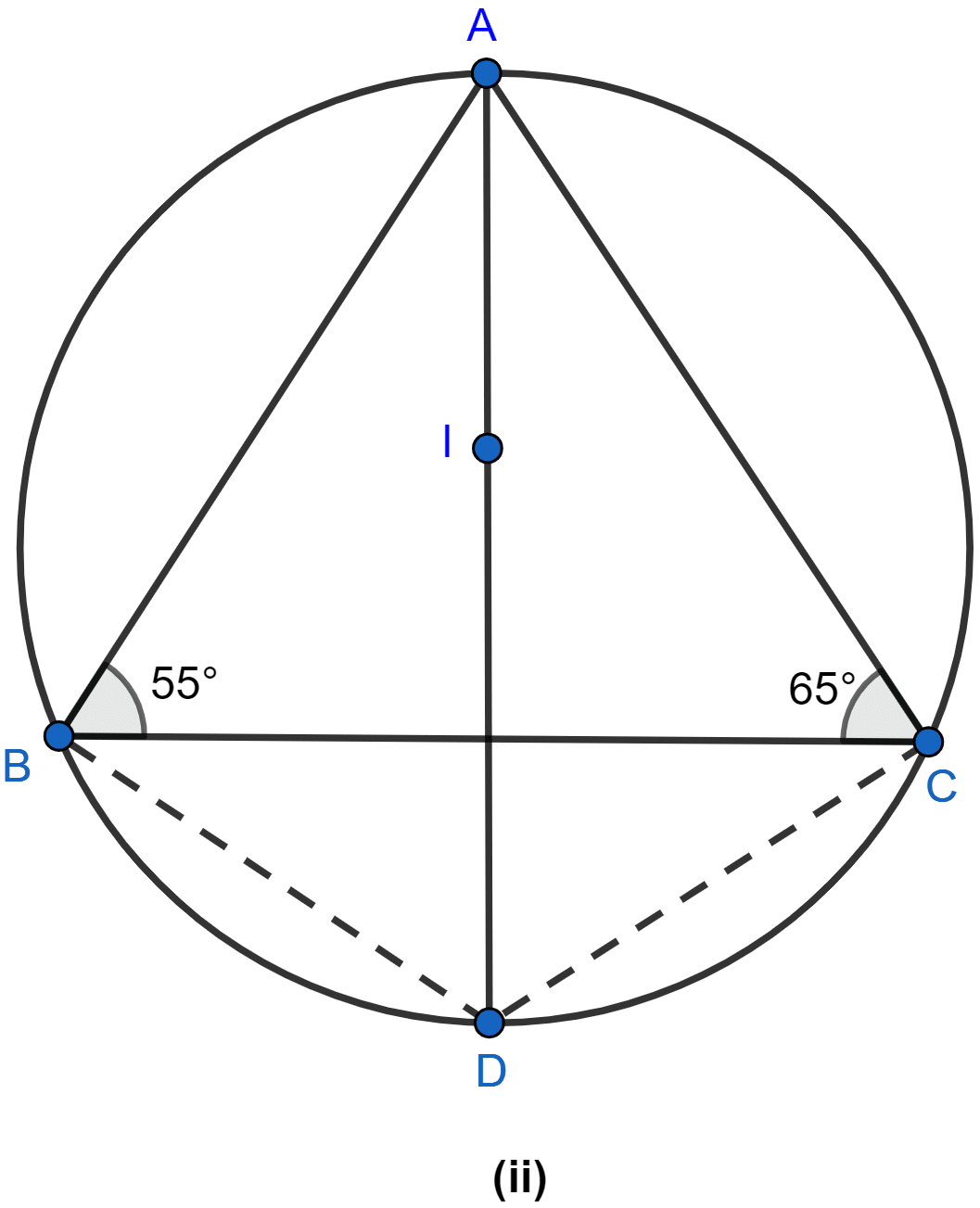
In the figure (ii) given below, I is the incentre of △ABC. AI produced meets the circumcircle of △ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.