Mathematics
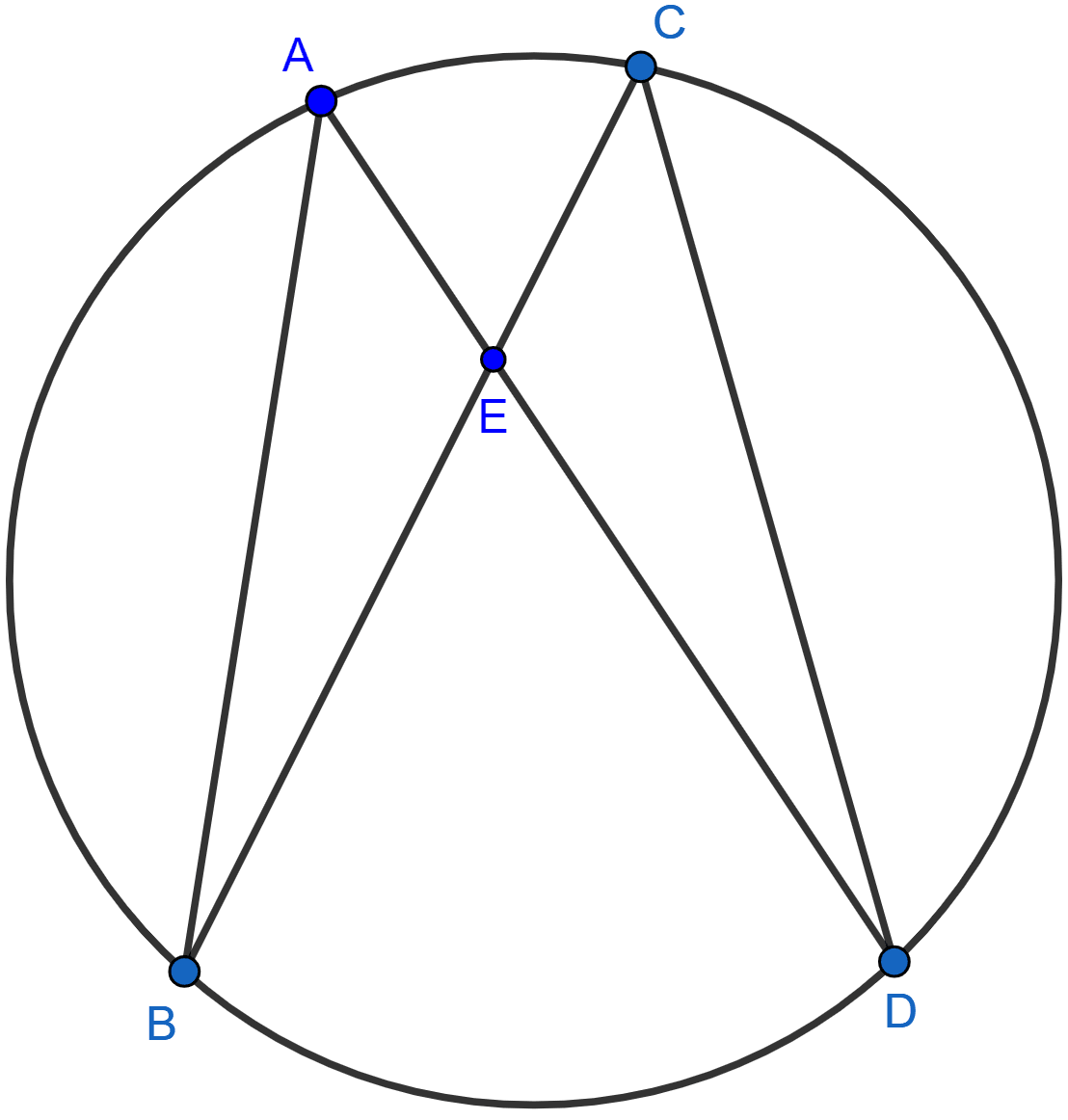
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.
Circles
48 Likes
Answer
In △AEB and △CED,
∠A = ∠C (∵ angles in same segment of a circle are equal.)
∠B = ∠D (∵ angles in same segment of a circle are equal.)
AB = CD (Given)
∴ △AEB ≅ △CED (By ASA axiom)
As corresponding part of congruent triangles are congruent hence,
AE = CE and BE = DE.
Hence, proved that AE = CE and BE = DE.
Answered By
26 Likes
Related Questions
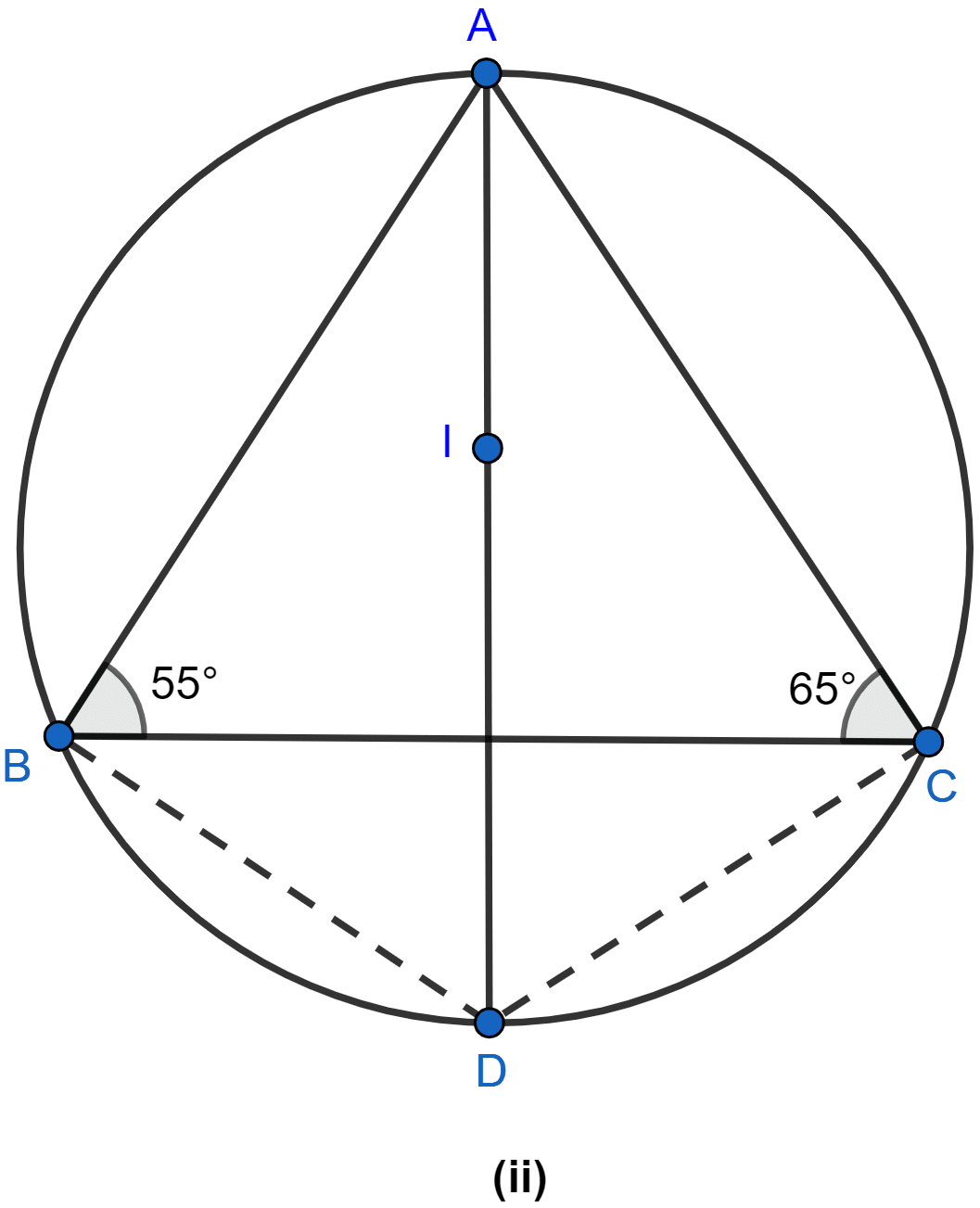
In the figure (ii) given below, I is the incentre of △ABC. AI produced meets the circumcircle of △ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
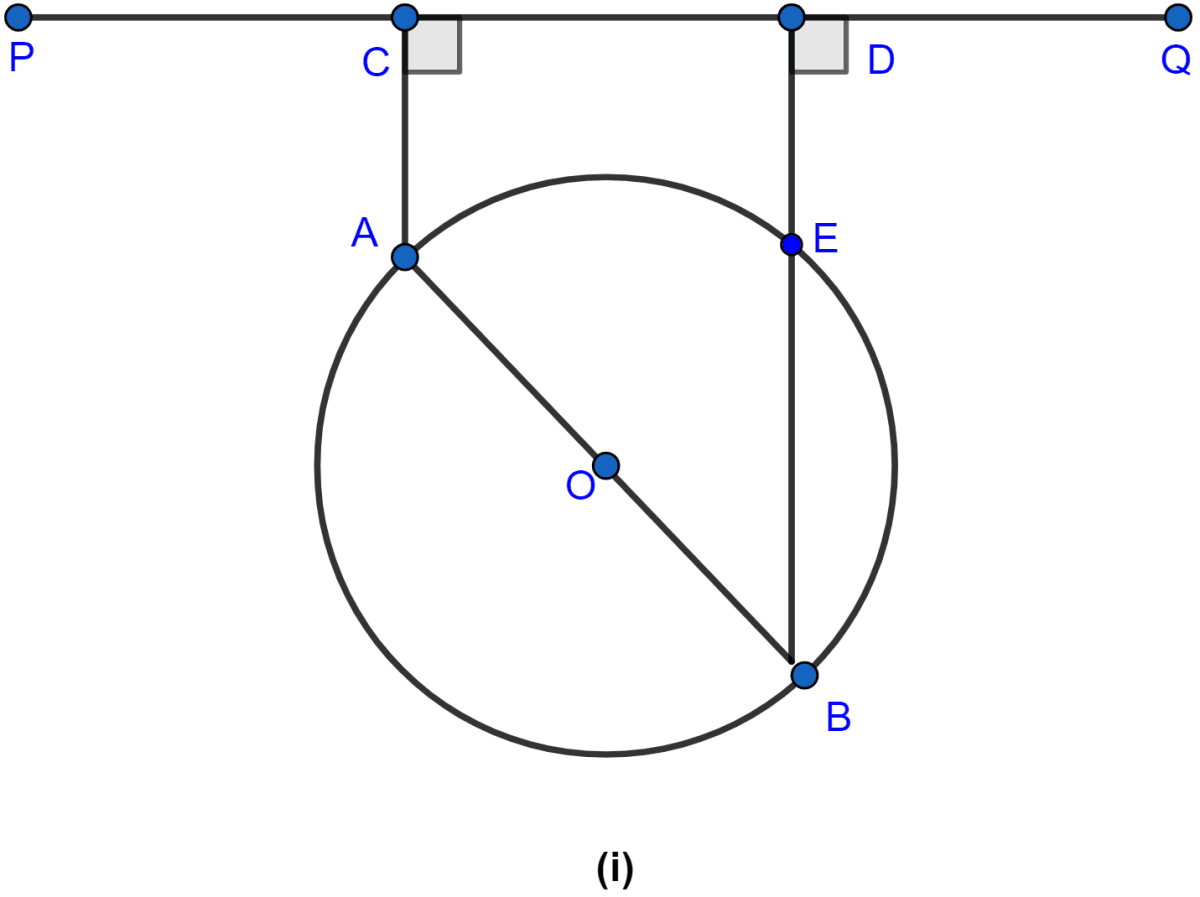
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
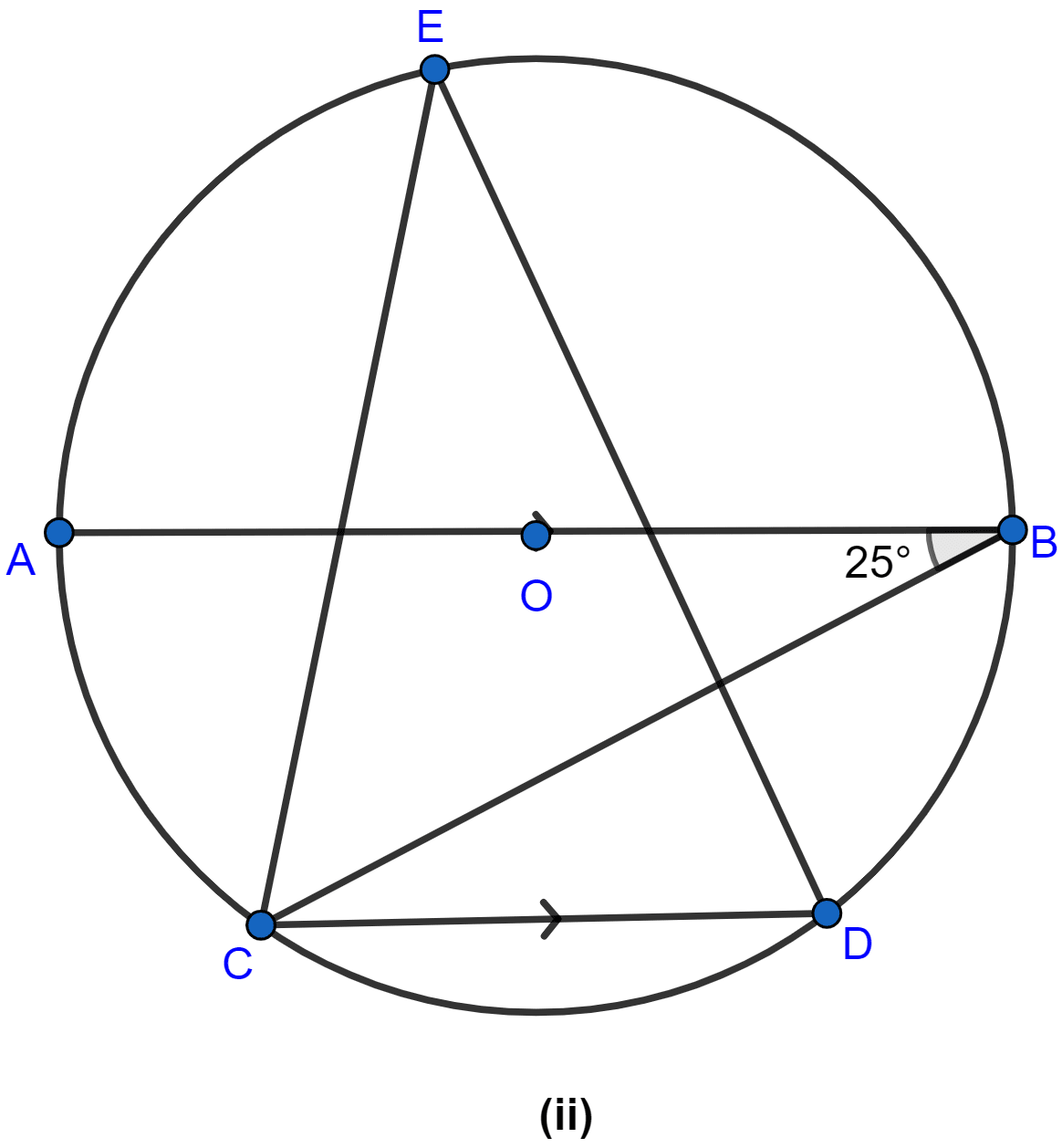
In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.