Mathematics
In △PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a - b) = (c + d)(c - d).
Pythagoras Theorem
Answer
In right angle △PDQ,
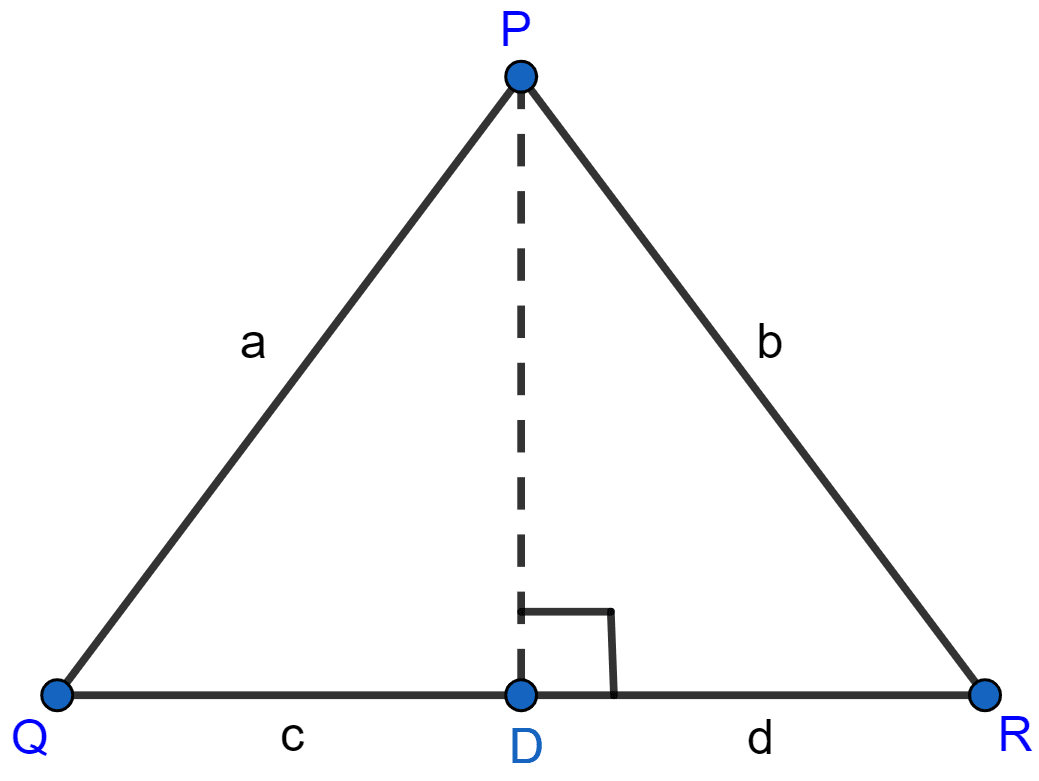
By pythagoras theorem we get,
⇒ PQ2 = PD2 + QD2
⇒ a2 = PD2 + c2
⇒ PD2 = a2 - c2 ……..(i)
In right angle △PDR,
By pythagoras theorem we get,
⇒ PR2 = PD2 + DR2
⇒ b2 = PD2 + d2
PD2 = b2 - d2 ……..(ii)
From (i) and (ii) we get,
⇒ a2 - c2 = b2 - d2
⇒ a2 - b2 = c2 - d2
⇒ (a - b)(a + b) = (c - d)(c + d).
Hence, proved that (a - b)(a + b) = (c - d)(c + d).
Answered By
Related Questions
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
In a triangle ABC, AD is perpendicular to BC. Prove that AB2 + CD2 = AC2 + BD2.
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. Find the altitude on BC and hence calculate its area.
Find the area and the perimeter of a square whose diagonal is 10 cm long.