Mathematics
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
Pythagoras Theorem
30 Likes
Answer
Since, the triangle is right triangle.
Hence, the side opposite to right angle will be hypotenuse and will be the greatest side.
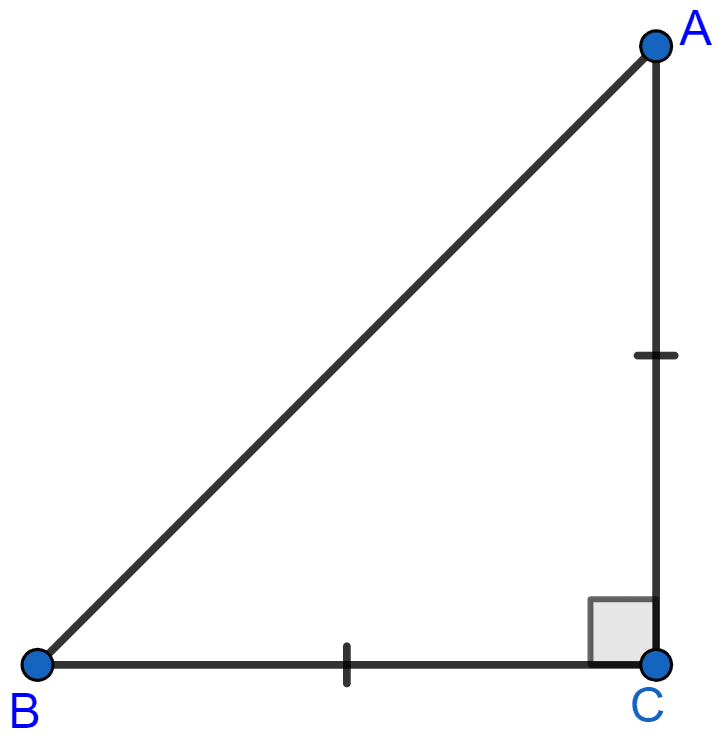
From figure,
Hypotenuse = AB.
The other two sides will be equal as the triangle is also isosceles i.e. (AC = BC)
By pythagoras theorem,
⇒ (AB)2 = (AC)2 + (BC)2
⇒ (AB)2 = (AC)2 + (AC)2
⇒ (AB)2 = 2AC2.
Hence, proved that (AB)2 = 2AC2.
Answered By
22 Likes
Related Questions
For going to a city B from the city A, there is route via city C such that AC ⊥ CB. AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of highway.
The hypotenuse of a right triangle is 6 m more than twice the shortest side. If the third side is 2m less than the hypotenuse, find the sides of the triangle.
In a triangle ABC, AD is perpendicular to BC. Prove that AB2 + CD2 = AC2 + BD2.
In △PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a - b) = (c + d)(c - d).