Mathematics
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
Similarity
22 Likes
Answer
ΔABC is shown in the figure below:
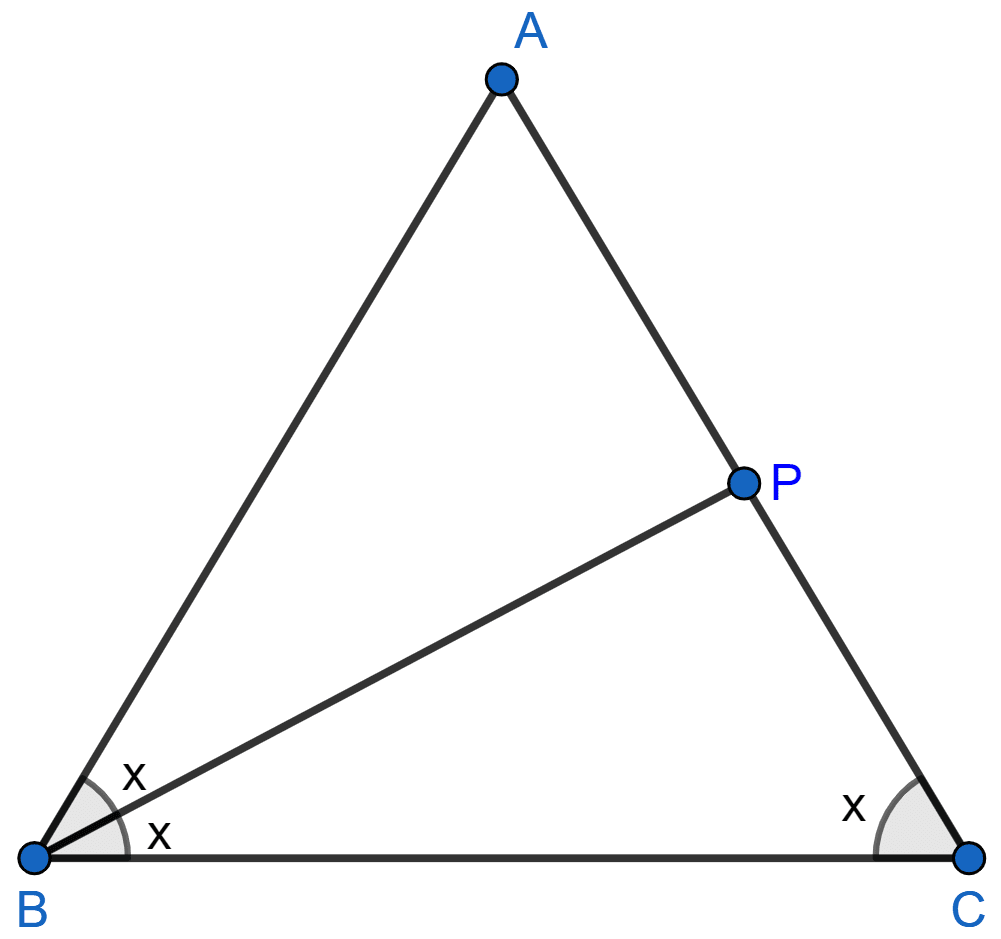
(i) Let ∠ACB = x, so ∠ABC = 2x.
Since, BP is the bisector of ∠ABC.
So, ∠ABP = ∠PBC = x.
By angle bisector theorem,
The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
i.e. CB : BA = CP : PA.
Hence, proved that CB : BA = CP : PA.
(ii) From figure,
∠APB = ∠PBC + ∠PCB = 2x. [Exterior angle is equal to the sum of opposite two interior angles].
∴ ∠APB = ∠ABC
∠BCP = ∠ABP [Both = x]
∴ △ABC ~ △APB [By A.A.]
Since corresponding sides of similar triangles are proportional we have,
⇒
⇒ AB x BC = BP x CA
Hence, proved that AB x BC = BP x CA.
Answered By
16 Likes
Related Questions
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ΔAPB is similar to ΔCPD.
(ii) PA x PD = PB x PC.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
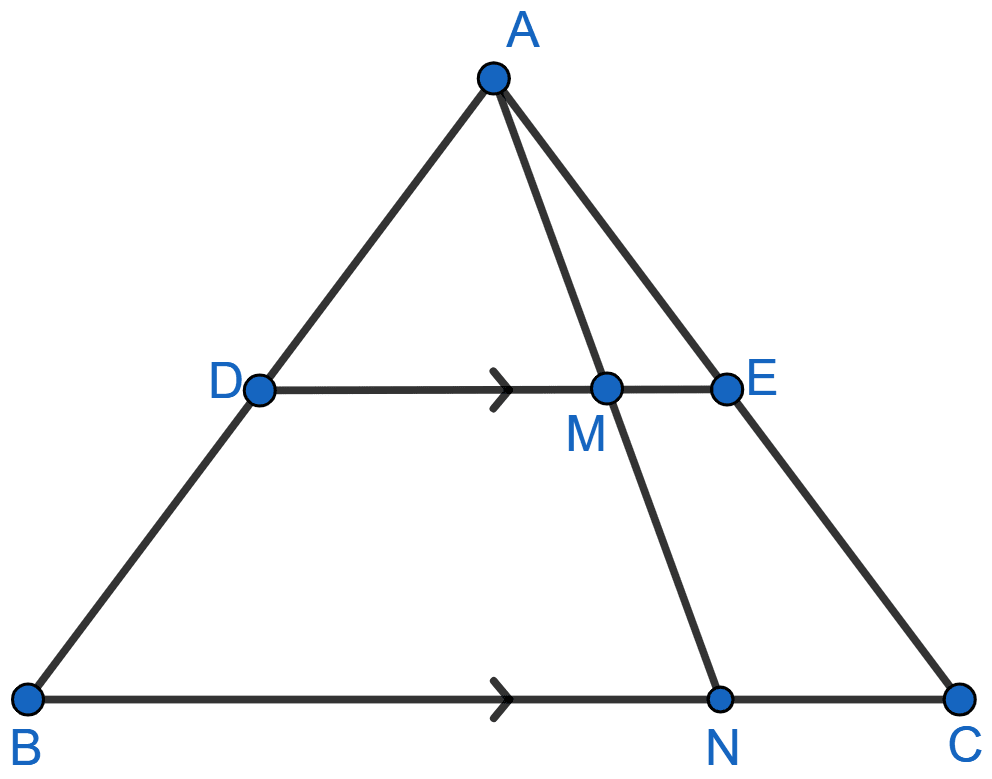
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.